Явище змочування. Капілярність
ВЛАСТИВОСТІ ГАЗІВ, РІДИН, ТВЕРДИХ ТІЛ*
Урок № 15
Тема. Явище змочування. Капілярність
Мета: ознайомити учнів із явищами змочування й капілярності.
Тип уроку: комбінований.
Обладнання: розплавлений парафін, картон, ножиці, дріт, мило, вода в посудині.
Найголовніше мислення не може дати жодних знань про світ фактів.
Пізнання реального світу виходить із дослідів і закінчується ними.
А. Ейнштейн
ХІД УРОКУ
I. Розминка
Вправа “Знайди зайве”
Психрометр, гігрометр, амперметр, термометр. (Амперметр)
Роса,
II. Актуалізація опорних знань
Робота учнів по групах
Провести дослід та пояснити його фізичний зміст.
І група
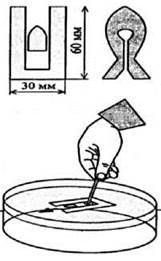
Із тонкого картону виріжте фігури, які зображено на рисунку. Занурте їх у розплавлений парафін. Після того як фігури охолонуть, пустіть їх плавати на поверхню води, налитої у скляну посудину. Паличкою, кінець якої був змочений у мильному розчині, торкніться води, як зображено на рисунку. “Снаряд” вилетить із ” гармати “. Якщо торкнутися води всередині “риби”, то вона попливе.
1. Навіщо було змочувати фігури у розплавленому
2. Що спричиняє рух “снаряда” і “риби”?
3. Що станеться, якщо торкнутись паличкою води в місці перед “снарядом”?
(Утому місці, куди потрапляє мильний розчин, поверхневий
Натяг зменшується, і тоді частина плівки води, поверхневий натяг якої більший, скорочуючись, тягне за собою фігури, що плавають.)
II група
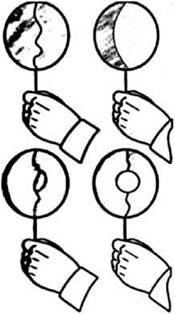
Зробіть із дроту кільце діаметром 10-15 см. Прив’яжіть до нього нитку так, щоб вона з’єднала протилежні сторони кільця. Довжина нитки повинна бути більшою за діаметр, але меншою за половину довжини кільця. Утворіть мильну плівку, зануривши кільце з ниткою у мильний розчин.
Якщо проштрикнути плівку з однієї сторони, то інша утворить з ниткою півмісяць.
Якщо у плівці розташувати петлю і зруйнувати плівку всередині неї, петля утворить форму кола.
1. Чому, якщо зруйнувати плівку з однієї сторони нитки, то інша утворить форму півмісяця?
2. Чому петля з нитки набуває форми саме кола, а не іншої фігури?
3. Коли сили поверхневого натягу були більшими – на початку стискання плівки чи наприкінці?
(Дія сил поверхневого натягу призводить до того, що плівка намагається зменшити площу своєї поверхні. Зруйнувавши плівку з однієї сторони, ми даємо змогу плівці, що залишилася, зменшити свою поверхню, стягнувшись у формі півмісяця. У другому випадку плівка розтягує петлю з нитки в усіх напрямах.)
III. Вивчення нового матеріалу
Дослід. Зануримо у воду пластилінову кульку. Як бачимо, кулька не мокра. Чому?
А коли зануримо кульку з паперу, то вона промокне. Чому?
У першому випадку, витягаючи кульку з води, ми відриваємо частинки рідини від частинок твердого тіла, а в другому – частинки рідини одна від одної. Це пояснюється відмінністю в силах зчеплення.
Якщо сили зчеплення частинок рідини й твердого тіла більші за сили зчеплення частинок рідини, рідина називається змочувальною, тобто такою, що змочує дане тверде тіло.
Якщо сили зчеплення частинок рідини й твердого тіла менші за сили зчеплення частинок рідини, рідина називається незмочувальною.
Явище змочування призводить до викривлення поверхні рідини біля поверхні твердого тіла. Явище змочування характеризується крайовим кутом?.
Для змочувальної рідини крайовий кут гострий: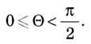 
Для незмочувальної – тупий: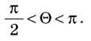 
Явище повного розтікання рідини називається повним змочуванням: ? = 0. Воно характерне, наприклад, для води, що знаходиться на чистому склі.
Випадок? =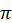 
відповідає повному незмочуванню твердого тіла рідиною. Воно спостерігається, наприклад, у разі контакту води й парафіну.
Явище змочування використовують під час склеювання, паяння, фарбування тіл. Явище змочування необхідно враховувати під час конструювання космічних апаратів, оскільки в стані невагомості змочувальна рідина розтікається по стінках посудини, в якій міститься, а незмочувальна – збирається великою краплею усередині посудини.
Тоненькі трубки, де рідина внаслідок змочування (чи незмочування) піднімається (чи опускається), називають капілярами, а явище підняття (чи опускання) рідини в них – капілярністю.
Опустимо таку трубку в рідину.
Дослід. Дуже тонку трубку опустити в воду. Вода піднімається по стінці трубки вище над рівнем рідини в посудині.
Але якщо взяти трубку трішки ширшу, то рідина піднімається над рівнем рідини в посудині менше, ніж у вузькій.
Висновок: якщо рідина змочує стінки трубки, то вона піднімається по стінці трубки над рівнем рідини в посудині й притому тим вище, чим вужча трубка.
Якщо рідина не змочує стінки, то, навпаки, рівень рідини у вузькій трубці встановлюється нижче, ніж у широкій посудині.
Встановлено, що тиск під увігнутою поверхнею менший, а під опуклою – більший, ніж під плоскою. Це можна уявити собі так, що під опуклою поверхнею рідини створюється додатковий тиск, що діє вниз. Цей додатковий тиск залежить як від поверхневого натягу, так і від форми поверхні.
Якщо позначити тиск під кривою поверхнею р; тиск під плоскою поверхнею р0, то різницю р – р0 називають капілярним тиском.
Тоді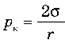 
, тобто капілярний тиск пропорційний поверхневому натягу рідини й обернено пропорційний радіусу кривизни поверхні.
Рівновага рідини настає тоді, коли піднятий стовп рідини своїм ваговим тиском зрівноважить капілярний тиск:
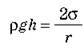, звідки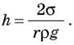 
Викривлену поверхню рідини в капілярах або біля стінок посудини називають меніском.
У змочувальної рідини меніск увігнутий, у незмочувальної – опуклий.
Додатковий тиск, зумовлений кривиною поверхні рідини, визначається за формулою Лапласа:
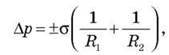
Де R1, R2 – радіуси кривизни двох взаємно перпендикулярних перетинів поверхні рідини; знак “+” для опуклого меніска, “-” для ввігнутого.
Повідомлення про відкриття капілярних явищ та їх використання
Першовідкривачем капілярних явищ вважається Леонардо да Вінчі. Однак перші акуратні спостереження капілярних явищ на трубках і скляних пластинках були виконані Френсисом Хоксбі 1709 року. Як часто буває, термодинамічний опис виявляється більш простим і більш загальним, не будучи обмеженим недоліками конкретних моделей.
Саме в такий спосіб описав капілярність Гіббс у 1878 р., побудувавши суто термодинамічну теорію. Ця теорія стала невід’ємною частиною гіббсовської термодинаміки. Теорія капілярності Гіббса, не спираючись безпосередньо на які-небудь механістичні моделі, позбавлена недоліків теорії Лапласа; вона може по праву вважатися першою детально розвиненою термодинамічною теорією поверхневих явищ.
Про теорію капілярності Гіббса можна сказати, що вона дуже проста і дуже складна. Проста тому, що Гіббсу удалося знайти метод, що дозволяє одержати найбільш компактні і витончені термодинамічні співвідношення, однаковою мірою застосовні до плоских і скривлених поверхонь.
Капілярні явища мають велике значення в природі і техніці. Завдяки цим явищам відбувається проникнення вологи з грунту в стебла і листя рослин. Саме в капілярах відбуваються основні процеси, пов’язані з диханням і живленням організмів. У тілі дорослої людини приблизно 160-109 капілярів, загальна довжина яких сягає 60-80 тис. км.
У будівництві враховують можливість підняття вологи по капілярних порах будівельних матеріалів. Для захисту фундаменту і стін від дії грунтових вод та вологи застосовують гідроізоляційні матеріали: толь, смоли тощо.
Завдяки капілярному підняттю вдається фарбувати тканини.
Часто капілярні явища використовують і в побуті. Застосування рушників, серветок, гігроскопічної вати, марлі, промокального паперу можливе завдяки наявності в них капілярів.
Капілярні явища використовуються під час видобування нафти. Сили взаємодії води з гірською породою більші, ніж у нафти. Тому вода здатна витиснути нафту з дрібних тріщин у більш великі. Для збільшення нафтовіддачі шарів використовуються спеціальні поверхнево-активні речовини.
Нафта має неоднакові оптичні властивості.
Під дією ультрафіолетових променів нафта здатна світитися.
При цьому легкі нафти світяться блакитним світлом, важкі – бурим і жовто-бурим. Це використовується під час пошуку нафти. Нафта є діелектриком і має високий питомий опір. На цьому засновані електрометричні методи встановлення в розрізі, розкритому свердловиною, нафтоносних шарів, ярів.
Як видно з наведеного історичного огляду, капілярні явища вивчаються вже протягом майже трьохсот років. За цей час досить помітно змінилися способи опису капілярних і поверхневих сил. Однак цікаво відзначити, що, починаючи з найперших робіт з теорії капілярних явищ, люди цілком правильно відносили їх до макроскопічних проявів сил, що діють між частинками в речовині. З розвитком уявлень про ці сили мінялося і розуміння їхньої ролі в тих чи капілярних явищах.
Теорія Гіббса дала цілком новий інструмент дослідження поверхневих явищ. З використанням потужного й універсального апарату термодинаміки удалося дати більш строгі визначення поняттям границі розподілу фаз, товщини плівки і т. ін. Крім того, формула Лапласа для різниці тисків у фазах поблизу скривленої поверхні була отримана в теорії Гіббса без усіляких додаткових припущень про радіус дії міжмолекулярних сил. Підхід, розвинений Гіббсом, і сьогодні не утрачає своєї актуальності в силу своєї універсальності і дивної широти охоплення явищ.
Сьогодні дослідження в галузі капілярних і поверхневих сил продовжуються, що обумовлено як їхньою важливістю в різних галузях науки, так і широким спектром практичних додатків.
IV. Узагальнення знань. Осмислення об’єктивних зв’язків
Розв’язати задачі.
1. Корковий кубик із ребром 2 см плаває у воді. Визначити глибину його занурення у воду, вважаючи змочування повним.
2. Знайдіть масу води, що піднялася по капіляру, діаметр якого 0,64 мм.
V. Підсумок уроку
Вікторина за запитаннями
– У посудину з гарячою водою опущена капілярна трубка.
– Як зміниться рівень води в трубці під час охолодження води?
– Яку рідину можна налити в склянку вище за його вінця?
– Наведіть приклади змочування і незмочування.
– Який тиск називають капілярним?
– Для чого враховують явище змочування?
VI. Домашнє завдання
Розв’язати задачі.
1. Тонка сталева голка може “лежати” на поверхні води. Чи вдасться цей дослід, якщо заздалегідь голку ретельно протерти одеколоном?
2. У спирт опущена трубка. Діаметр її внутрішнього каналу дорівнює 0,5 мм. На яку висоту підніметься спирт у трубці? Густина спирту 800 кг/м3.
(1 votes, average: 5.00 out of 5)
Loading...