ЗАКОН ЗБЕРЕЖЕННЯ І ПЕРЕТВОРЕННЯ МЕХАНІЧНОЇ ЕНЕРГІЇ
РОЗДІЛ 4 МЕХАНІЧНА РОБОТА ТА ЕНЕРГІЯ
& 33. ЗАКОН ЗБЕРЕЖЕННЯ І ПЕРЕТВОРЕННЯ МЕХАНІЧНОЇ ЕНЕРГІЇ
Мабуть, кожен із вас грався з м’ячиком-стрибунцем. Згадайте: м’ячик злітає вгору, падає на підлогу, відскакує від неї, знову злітає і знову падає… Коли м’ячик летить угору, швидкість його руху зменшується, потім м’ячик на мить зупиняється на певній висоті, а після цього починає рух униз. Кінетична енергія м’ячика під час руху вгору теж зменшується. А чи зникає енергія м’ячика зовсім?
1. Досліджуємо
Одним із фундаментальних законів природи є закон збереження і перетворення енергії:
Енергія нікуди не зникає і нізвідки не виникає, вона лише перетворюється з одного виду на інший, передається від одного тіла до іншого.
Для прикладу розглянемо перетворення потенціальної енергії на кінетичну і навпаки під час вільних коливань маятника (рис. 33.1). Вважатимемо, що тертям можна знехтувати.
За нульовий рівень оберемо найнижче положення кульки – положення рівноваги (на рис. 33.1 – положення 2).
Відхилимо кульку до положення 1. У нашому
У момент, коли кулька опиняється в положенні 2, її потенціальна енергія зменшується до нуля (h = 0, Ep = mgh = 0). У цей момент швидкість руху кульки є найбільшою і також найбільшою є її кінетична енергія
(Еkmax =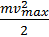 
).
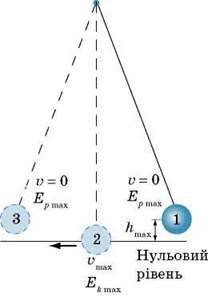
Рис. 33.1. Під час коливань нитяного маятника відбувається постійне перетворення потенціальної енергії кульки на кінетичну енергію і навпаки
За рахунок запасу кінетичної енергії кулька продовжує рух, піднімаючись усе вище, внаслідок чого зростає її потенціальна енергія. Натомість швидкість руху кульки зменшується, відповідно зменшується її кінетична енергія.
Нарешті кулька зупиниться в положенні 3 – на висоті hmax. Кінетична енергія кульки перетвориться на нуль, а потенціальна енергія сягне найбільшого значення.
Таким чином, під час коливань маятника один вид механічної енергії переходить в інший: потенціальна енергія перетворюється на кінетичну і навпаки.
Спробуйте пояснити перетворення енергії під час коливань пружинного маятника (рис. 33.2).
Рис. 33.2. Взаємне перетворення потенціальної і кінетичної енергій триватиме доти, доки коливається іграшка
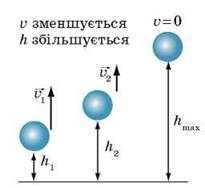
Рис. 33.3. Під час руху м’ячика вгору його потенціальна енергія збільшується, а кінетична – зменшується (коли м’ячик рухається вниз, Ek збільшується, Ep зменшується)
2. Відкриваємо закон збереження і перетворення механічної енергії
Повернемося до прикладу з м’ячиком – стрибунцем. Коли м’ячик летить угору, висота, на якій він перебуває, зростає, тобто зростає і його потенціальна енергія (рис. 33.3). Швидкість руху м’ячика зменшується, відповідно зменшується його кінетична енергія. За умови відсутності сили опору повітря кінетична енергія м’ячика зменшується на стільки, на скільки збільшується його потенціальна енергія, і навпаки, тобто повна механічна енергія системи м’ячик-Земля не змінюється.
Те саме можна сказати й про маятники під час їхніх коливань: за відсутності сил тертя повна механічна енергія маятників залишається незмінною.
Теоретичні та експериментальні дослідження дозволили сформулювати закон збереження і перетворення механічної енергії:
У системі тіл, які взаємодіють одне з одним тільки силами пружності та силами тяжіння, повна механічна енергія не змінюється:
Ek0 + Ep0 = Ek + Ep,
Де Ek 0 + Ep0 – повна механічна енергія системи тіл на початку спостереження; Ek + Ep – повна механічна енергія системи тіл в кінці спостереження.
3. Дізнаємося, що відбувається з енергією, якщо в системі існують сили тертя
Наголосимо ще раз: закон збереження і перетворення механічної енергії* справджується лише у випадках, коли немає втрат механічної енергії, зокрема за умови відсутності тертя. Якщо в системі існує тертя, то механічна енергія (або її частина) перетворюється на внутрішню*.
Як приклад розглянемо перетворення механічної енергії на внутрішню під час гальмування потяга. Коли машиніст натискає на гальмо, гальмівні колодки притискаються до коліс (рис. 33.4). Унаслідок дії сили тертя ковзання швидкість обертання колеса, а отже, й швидкість руху потяга зменшуються, тобто зменшується його механічна енергія. При цьому, якщо доторкнутися до гальмівних колодок або колеса відразу після гальмування, то можна навіть обпектися – так сильно вони нагріваються. Нагрівання свідчить про те, що внутрішня енергія цих тіл збільшилась.
Отже, кінетична енергія потяга перетворилася на внутрішню енергію гальмівних колодок, колеса та навколишнього середовища.
Рис. 33.4. Колесо потяга під час гальмування
* Закони, про які йшлося в пунктах 1 і 2 параграфа, для скорочення зазвичай будемо називати “закон збереження енергії” і “закон збереження механічної енергії”.
* Внутрішня енергія тіла – це енергія руху та взаємодії молекул (атомів, йонів), з яких складається тіло. Зі збільшенням температури тіла його внутрішня енергія збільшується. Докладніше про внутрішню енергію ви дізнаєтесь у 8 класі.
4. Учимося розв’язувати задачі
Задача 1. Тіло масою 1 кг починає падати на поверхню Землі з висоти 20 м. На якій висоті кінетична енергія тіла дорівнюватиме 100 Дж? Опором повітря знехтуйте.
Аналіз фізичної проблеми. За відсутності опору повітря повна механічна енергія системи тіло – Земля не змінюється, тому для розв’язання задачі можемо скористатися законом збереження механічної енергії. Тіло починає рух, тому його початкова швидкість дорівнює нулю: v0 = 0.
Виконаємо пояснювальний Малюнок, на якому зазначимо положення тіла на початку та в кінці спостереження. За нульовий рівень оберемо поверхню Землі. Задачу розв’язуватимемо в одиницях СІ.
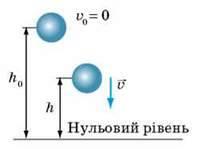
Дано:
M = 1 кг
V0 = 0
H0 = 20 м
Ek = 100 Дж
G = 10кг
Знайти:
H – ?
Пошук математичної моделі, розв’язання. За законом збереження механічної енергії:
Ek 0 + Ep0 = Ek + Ep.
На початковій висоті h0:
На шуканій висоті h:
Ek = 0 = 0 (адже v0 = 0);
Ep 0 = mgh0.
Ek ≠ 0 (адже тіло рухається);
Ep = mgh.
Отже: 0 + mgh0 = Ek + mgh.
Звідси маємо: mgh = mgh0 – Ek => h = h0 –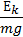 
.
Перевіримо одиниці, визначимо значення шуканої величини:
[h] = м –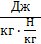 
= 
– 
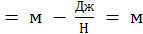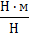= м;
H = 20 –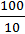 
= 20 – 10 = 10 (м).
Відповідь: h = 10 м.
Задача 2. Тіло кидають вертикально вгору зі швидкістю 20 м/с. На якій висоті потенціальна енергія тіла дорівнюватиме його кінетичній енергії? Опором повітря знехтуйте.
Аналіз фізичної проблеми. Оскільки опором повітря ми нехтуємо, то повна механічна енергія системи тіло-Земля не змінюється, тому для розв’язання задачі можемо скористатися законом збереження механічної енергії. Рівень, з якого кидають тіло, візьмемо за нульовий. Задачу розв’язуватимемо в одиницях СІ.
Дано:
V0= 20 
Ep = Ek
G = 10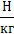 
H0 = 0
Знайти:
H – ?
Пошук математичної моделі, розв’язання. За законом збереження механічної енергії:
Ek 0 + Ep0 = Ek + Ep.
На початковій висоті h0:
Ek0 =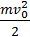 
.
Ep 0 = 0 (адже h0 = 0).
На шуканій висоті h:
Ek = Ep – за умовою;
Ep = mgh.
Отже, маємо: 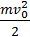= mgh + mgh.
З отриманого рівняння визначимо шукану висоту:
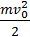= 2mgh => mv20 = 4mgh, звідки h = 
.
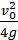Визначимо значення шуканої величини:
H =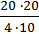 
= 
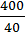= 10 (м).
Відповідь: h =10 м.
Підбиваємо підсумки
Потенціальна енергія тіла (системи тіл) може перетворюватися на кінетичну енергію, і навпаки.
Закон збереження і перетворення механічної енергії: у системі тіл, які взаємодіють одне з одним тільки силами пружності та силами тяжіння, повна механічна енергія не змінюється:
Ek0 + Ep0 = Ek + Ep.
Якщо в системі існує тертя, то повна механічна енергія з часом зменшується: частина механічної енергії перетворюється на внутрішню.
Контрольні запитання
1. Наведіть приклади перетворення потенціальної енергії тіла на кінетичну і навпаки. 2. Сформулюйте закон збереження механічної енергії. 3. За яких умов виконується закон збереження механічної енергії? 4. Наведіть приклади, коли повна механічна енергія не зберігається. Чи порушується при цьому закон збереження енергії?
Вправа № 33
1. Шайба скочується з льодової гірки на асфальт і зупиняється. Чи зберігається в цьому випадку повна механічна енергія?
2. Пружинний пістолет заряджають кулькою і стріляють угору. Які перетворення енергії при цьому відбуваються?
3. Початкова потенціальна енергія тіла, яке перебуває на деякій висоті в стані спокою, дорівнює 400 Дж. Тіло відпускають. Якою буде кінетична енергія тіла в момент, коли його потенціальна енергія становитиме 150 Дж? Опором повітря знехтуйте.
4. Тіло кидають угору, надаючи йому кінетичну енергію 300 Дж. На якійсь висоті кінетична енергія тіла зменшиться до 120 Дж. Якою буде потенціальна енергія тіла на цій висоті? Опором повітря знехтуйте.
5. Камінь масою 500 г кинули вертикально вгору зі швидкістю 20 м/с. Визначте кінетичну і потенціальну енергії каменя на висоті 10 м.
6. Тіло, що перебувало в стані спокою, падає з висоти 20 м. На якій висоті швидкість руху тіла дорівнюватиме 10 м/с? Опором повітря знехтуйте.
7. М’яч кинули вертикально вгору зі швидкістю 8 м/с. Визначте, на який висоті швидкість руху м’яча зменшиться вдвічі. Опором повітря знехтуйте.
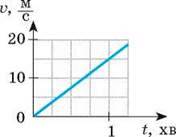
8. На рисунку подано графік залежності швидкості руху вантажівки масою 4 т від часу. Визначте кінетичну енергію вантажівки через 15 с після початку спостереження.
Експериментальне завдання
Підкиньте вгору якесь невеличке тіло (наприклад, сірникову коробку) і спіймайте його. Спробуйте визначити початкову швидкість руху тіла та швидкість руху тіла в момент дотику до вашої руки. Висоту, на яку піднялося тіло, виміряйте або оцініть “на око”. Опором повітря знехтуйте.
Фізика і техніка в Україні
Один із видатних фізиків сучасності – Лев Давидович Ландау (1908-1968) – продемонстрував свої неабиякі здібності ще в середній школі. Після закінчення університету він стажувався в одного з творців квантової фізики Нільса Бора. Уже в 24 роки Л. Д. Ландау очолив теоретичний відділ Українського фізико-технічного інституту (УФТІ) в Харкові та кафедру теоретичної фізики в Харківському політехнічному інституті, а згодом – кафедру теоретичної фізики Харківського університету.
В УФТІ Л. Д. Ландау створив відому школу теоретичної фізики. Його першими учнями були О. С. Компанєєць, Є. М. Ліфшиць, О. І. Ахієзер, І. Я. Померанчук. У 1937 р. на запрошення академіка П. Л. Капіци Ландау перейшов на роботу в Інститут фізичних проблем.
Як і більшість видатних фізиків-теоретиків, Ландау вирізнявся надзвичайною широтою наукових інтересів. Ядерна фізика, фізика плазми, теорія надплинності рідкого гелію, теорія надпровідності – в усі ці розділи фізики Ландау зробив значний внесок. У 1962 р. за роботи з фізики низьких температур Л. Д. Ландау отримав Нобелівську премію.
(1 votes, average: 5.00 out of 5)
Loading...