ЗАКОН ЗБЕРЕЖЕННЯ МЕХАНІЧНОЇ ЕНЕРГІЇ
Розділ IV Механічна робота та енергія
& 34. ЗАКОН ЗБЕРЕЖЕННЯ МЕХАНІЧНОЇ ЕНЕРГІЇ
Перетворення енергії
Перетворення енергії з одного виду в інший постійно відбуваються в природі і техніці. Перекриваючи ріку греблею гідроелектростанції, добиваються того, що вода піднімається на значну висоту і набуває величезної потенціальної енергії.
Падаючи вниз, вода збільшує свою кінетичну енергію, за рахунок якої вона обертає лопаті гідротурбін. Ті у свою чергу обертають електрогенератори, які виробляють електричну енергію.
Розглянемо
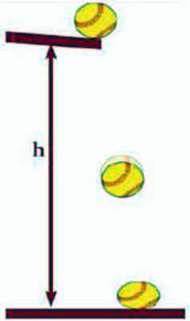
Мал. 34.1. Перехід потенціальної енергії м’яча в кінетичну енергію
Закон збереження енергії
Численні й досить точні досліди показали, що кінетична енергія збільшується
Якщо E1 = ЕК1 + ЕР1 – повна механічна енергія тіла в одному стані, а Е2 = ЕК2 + ЕР2 – в іншому стані, то E1 = Е2, тобто енергія зберігається за умови відсутності дії сил тертя.
Мал. 34.2. Потенціальна енергія деформованого лука перейшла у кінетичну енергію стріли, яка в свою чергу перейшла у потенціальну енергію тяжіння
Приклади розв’язування задач на застосування закону збереження енергії
Приклад 34.1
Швидкість стріли під час вистрілу з лука (мал. 34.2) становить 20 м/с. На яку найбільшу висоту вона може піднятися? g = 10 м/с2.
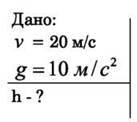
Розв’язання. За нульовий рівень потенціальної енергії вибираємо місце вистрілу. У такому випадку на момент вистрілу тіло мало лише кінетичну енергію і його повна енергія становить Е1 =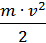 
.
При досягненні найвищої точки швидкість тіла стала рівною нулю і повна енергія складається тільки з потенціальної: Е2 = mgh. Сила тертя об повітря мала і нею можна знехтувати, тому E1 = Е2, що дає: 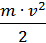= mgh. Звідси h = 
= 
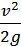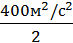∙10 м/с2 = 20 м.
Відповідь: За умови відсутності тертя, стріла може піднятися на висоту 20 м.
Обговорення результатів. а) Висота 20 м була досягнута за умови відсутності тертя (тобто втрат енергії). Реально, висота підйому буде дещо меншою. б) Маса тіла в процесі обрахунків скоротилася, це означає, що тіло довільної маси, якому надали швидкості 20 м/с, досягне висоти 20 м. Якщо цей факт вас дивує, то спробуйте вирішити цей парадокс.
Приклад 33.2
Тіло масою 3 кг падає з висоти 8 м. Якою буде його швидкість в момент торкання поверхні? g = 10 м/c2.
Розв’язання. Подібно до попередньої задачі, mgh = 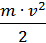, звідки:
V2 =2gh, v2 =2 ∙ 10 м/c2 ∙ 8м = 160m2 /с2. v = 16м/с.
Відповідь: тіло досягне швидкості 16 м/с.
Приклад 33.3
Іграшковий пружинний пістолет, жорсткість пружини якого 1 Н/см, зарядили кулькою масою 20 г і стиснули пружину на 10 см. З якою швидкістю вилетить кулька при пострілі?
Розв’язання. Перш ніж розв’язувати задачу, треба привести одиниці вимірювання в систему СІ: 1 Н/см = 100 Н/м, 20 г = 0,02 кг, 10 см = 0,1 м.
Енергія стисненої пружини становить E1 = 
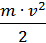∙ k ∙ х, коли пружина випрямилась, то потенціальна енергія деформації пружини перейшла вкінетичну енергію кульки, яка дорівнює Е2 = . Згідно із законом збереження енергії, повинна виконуватися рівність E1 = Е2 , тобто ∙ k ∙ х2 = 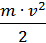. Звідси: v2 = 
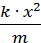, v2 = 
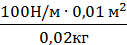= 50м2 / с2, v ≈ 7 м/с.
Відповідь: кулька матиме швидкість приблизно 7 м/с.
Енергія і робота
Нагадаємо, що роботу можна обчислити:
1. За формулою A = F ∙ S, якщо сила постійна. 2. За графіком сили – як площу під графіком.
3. Через потужність, як А = Р ∙ t. Виходячи з визначення енергії, можна ще одним способом обчислювати роботу: 4. Робота сили дорівнює зміні енергії тіла, яку вона спричинила.
Якщо повна енергія тіла збільшується, то це означає, що якась сила виконує позитивну роботу. Тоді збільшення повної енергії тіла дорівнює роботі цієї сили: А = Е2 – E1. Якщо повна енергія тіла зменшується, то це означає, що якась сила виконує негативну роботу. Сила тертя ковзання, наприклад, виконує від’ємну роботу і тому в рівності Атр=Е2 – Е1: Е2 < Е1.
Отже, зміна механічної енергії є наслідком виконання роботи, а виконання роботи приводить до зміни енергії.
Тема для дослідження
34.1. Дослідіть, як відбивається тенісний м’ячик від різних предметів: стола, зошита, килима, ракетки, камінців на березі річки, тощо. Чи може м’яч підскочити на висоту більшу, ніж та, з якої він впав?
Підведемо підсумки
– Енергія не виникає ні з чого і не зникає безслідно. Вона тільки переходить з одного виду в інший.
– Закон збереження механічної енергії: повна механічна енергія тіла не змінюється, якщо немає втрат на тертя.
– Механічна робота може бути обчислена як зміна повної механічної енергії.
Вправа 34
1. Які перетворення енергії відбуваються при падінні м’яча?
2. За рахунок якої енергії працюють турбіни ГЕС?
3. За яких умов зберігається повна механічна енергія тіла?
4. Якщо повна енергія тіла зберігається, то як змінюється потенціальна енергія тіла при зменшенні його кінетичної енергії?
5. Які способи обчислення механічної роботи ви знаєте?
6. М’яч падає з певної висоти. Як змінюються його: а) кінетична; б) потенціальна; в) повна енергія? Тертям можна нехтувати.
7. Чому м’яч, який упав з деякої висоти на землю і відскочив, уже не може піднятися на попередню висоту?
8. Чому м’яч, який упав у пісок, взагалі не підскакує?
9. Куди поділася потенціальна енергія тяжіння м’яча в момент найбільшої деформації при падінні на підлогу (мал. 34.1)?
10. Відомі висота, з якої упав м’яч, його маса і швидкість у момент падіння. Як можна знайти роботу сили тертя об повітря при падінні м’яча?
11. Яку швидкість треба надати м’ячикові, щоб підкинути його вгору на висоту 5 м? g = 10 м/с2.
12. Якої швидкості могла б набути краплина дощу, упавши з висоти 2 км, якби не було сил тертя й опору повітря? g = 10 м/с2.
13. Пружинний пістолет стріляє кульками масою 5 г. Перед вистрілом пружина жорсткістю 5 Н/см стискається на 10 см. а) Яку енергію має стиснута пружина? б) Яку швидкість має кулька в момент вильоту з дула? в) На яку максимальну висоту можна вистрілити таким пістолетом? g = 10 м/с2.
14. Яку роботу треба виконати, щоб натягнути тятиву лука у прикладі 34.1? Маса стріли становить 200 г.
15. Потенціальна енергія тіла при його падінні зменшилась на 20 Дж. На скільки збільшилась його кінетична енергія, якщо вважати, що тертя дуже мале?
16. Автомобіль масою 1,5 т збільшив швидкість з 36 км/год. до 54 км/год. за 5 с. Яку середню потужність розвивав при цьому двигун?
17. Стартують два автомобілі. За один і той самий час після старту перший набрав швидкість, удвічі більшу за швидкість другого. У скільки разів середня потужність двигуна першого автомобіля більша, ніж у двигуна другого автомобіля?
18. Швидкість автомобіля масою 5 тонн, що рухається горизонтальною дорогою, зменшилася з 72 км/год. до 54 км/год. Яку роботу виконала сила тертя?
19. Якій фізичній величині відповідає вираз: F ∙ s/t?
(1 votes, average: 5.00 out of 5)
Loading...