Закони випромінювання абсолютно чорного тіла
ФІЗИКА
Частина 4
ОПТИКА. СПЕЦІАЛЬНА ТЕОРІЯ ВІДНОСНОСТІ
Розділ 13 КОРПУСКУЛЯРНІ ВЛАСТИВОСТІ СВІТЛА
13.2. Закони випромінювання абсолютно чорного тіла
У багатьох випадках потрібно знати не лише спектральну густину випромінювання тіла (випромінювальну здатність), а й енергію, що випромінюється одиницею поверхні тіла за одиницю часу по всіх довжинах хвиль. Цю величину називають інтегральною випромінювальною здатністю, або енергетичною світністю тіла. Позначимо інтегральну випромінювальну здатність абсолютно чорного тіла

Де rλ,T – випромінювальна здатність, у певному спектральному інтервалі є функцією довжини хвилі й температури, а RT – функцією тільки температури.
Знайти аналітичний вираз функції rλ,T досить важко. Значно простіше визначити інтегральну випромінювальну здатність абсолютно чорного тіла, тобто RT. Для функції rλ,T порівняно просто визначити деякі важливі властивості. Для інтегральної випромінювальної здатності абсолютно чорного тіла австрійські фізики Й. Стефан (експериментально 1879 р.) і Л. Больцман

Де Т – абсолютна температура випромінювального тіла; σ – стала Стефана – Больцмана. Отже, закон Стефана – Больцмана можна сформулювати так: інтегральна випромінювальна здатність абсолютно чорного тіла пропорційна четвертому степеню його абсолютної температури. На основі численних дослідів доведено, що коефіцієнт пропорційності σ = 5,67 ∙ 10-8 Вт ∙ м-2 ∙ К-4.
Закон Стефана – Больцмана має велике значення, оскільки за високих температур випромінювання деяких тіл наближається до випромінювання абсолютно чорного тіла. Проте слід пам’ятати, що в загальному випадку закон Стефана – Больцмана не може бути застосованим до тіл, які не є абсолютно чорними, оскільки для таких тіл, як показує досвід, зі зміною температури змінюється і коефіцієнт σ, і показник степеня при температурі.
Закон Стефана – Больцмана стосується лише інтегральної випромінювальної здатності абсолютно чорного тіла і не дає ніяких відомостей про спектральний розподіл енергії. Проте такий розподіл існує і, як довели експериментальні дослідження, проходить через максимум. Виходячи з теоретичних міркувань, німецький фізик В. Він 1893 р. встановив важливий закон, що визначає положення цього максимуму в спектрі випромінювання абсолютно чорного тіла залежно від абсолютної температури. Аналітично цей закон можна записати так:

Де λm – довжина хвилі, яка відповідає максимуму випромінювальної здатності абсолютно чорного тіла; Т – його абсолютна температура; b – стала Віна, яка дорівнює 2,898 ∙ 10-3 м∙К. Отже, за законом зміщення Віна довжина хвилі, яка відповідає максимуму випромінювальної здатності абсолютно чорного тіла, обернено пропорційна абсолютній температурі.
Величина максимуму rmλ,T як показали вимірювання, прямо пропорційна п’ятому степеню абсолютної температури. Цю залежність називають ще третім законом випромінювання абсолютно чорного тіла. На рис. 13.1 зображено криві розподілу енергії в спектрі абсолютно чорного тіла за довжинами хвиль для двох температур T1 і Т2, причому Т2 > T1. Площа під кожною з цих кривих розподілу визначає сумарну енергію RT усіх довжин хвиль, що випромінюється одиницею поверхні абсолютно чорного тіла за 1 с. Із рис. 13.1 видно, що сумарна енергія збільшується з підвищенням температури, а максимум випромінювання зміщується в бік коротких хвиль. Кожній температурі відповідає певна довжина хвилі λm з максимальним значенням rmλ,T.
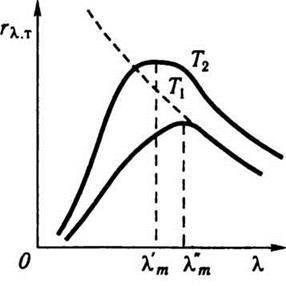
Рис. 13.1
На законі Віна грунтується так звана оптична пірометрія – метод визначення температури розжарених тіл за їхніми спектрами випромінювання. Саме таким методом було вперше визначено температуру поверхні Сонця. Розподіл енергії в спектрі випромінювання Сонця подібний до випромінювання абсолютно чорного тіла (якщо йдеться про випромінювання ядра Сонця, а не його поверхні). Максимум енергії випромінювання припадає на довжину хвилі λm = 470 нм. Отже, температура поверхні Сонця, за законом зміщення Віна, має дорівнювати 6160 К. Для тіл, що не є абсолютно чорними, цей метод не дає справжнього значення температури.