Додавання і віднімання цілих і дробових чисел
Урок № 19
Тема. Додавання і віднімання цілих і дробових чисел
Мета: продовжити роботу з відпрацювання навичок виконання додавання і віднімання дробів з різними знаменниками; розпочати роботу з формування вмінь використовувати відповідні алгоритми при додаванні і відніманні мішаних чисел.
Тип уроку: застосування вмінь і навичок.
Хід уроку
І. Перевірка домашнього завдання
@ Цей етап уроку можна провести у вигляді короткої самостійної роботи з подальшою перевіркою і обговоренням результатів.
Самостійна робота
Варіант 1 | Варіант 2 |
1. Виконайте дії: А) | 1. Виконайте дії: А) |
2. Обчисліть найзручнішим способом: А) В) 3. Знайдіть корінь рівняння:
| 2. Обчисліть найзручнішим способом: А) В) 3. Знайдіть корінь рівняння:
|
II. Актуалізація опорних знань
@ Під час обговорення результатів самостійної роботи учні ще раз повторюють алгоритми:
– знаходження НСК двох (кількох) чисел (для випадків, коли числа або взаємно прості, або одне кратне іншому, або вони мають НСД = 1 і не діляться одне на одне);
– зведення дробів до НСЗ;
– додавання і віднімання дробів з однаковими знаменниками; різними знаменниками;
– властивості додавання і віднімання;
– знаходження доповнення дробу до 1;
– робота з неправильним дробами.
Якщо всі ці моменти учнями засвоєні й відпрацьовані, слід звернути увагу на інший тип завдань цієї теми – додавання і віднімання мішаних чисел.
III. Доповнення знань учнів
@ Найпростіші приклади на додавання і віднімання мішаних чисел з однаковими знаменниками у дробових частинах учні розв’язували в 5 класі (і повторили під час розв’язання вправ). Тому вчителю слід нагадати спосіб обчислень (окремо – цілих, окремо – дробових частин) і поширити його на додавання і віднімання мішаних чисел з різними знаменниками. Також учителю слід чітко уявляти, які випадки є проблемними і відпрацювати їх на якомога більшій кількості прикладів. І останнє: робота з дробами не є цікавою для більшості учнів, тому для створення позитивної мотивації вчителю слід попрацювати над підбором різноманітних засобів зацікавлення учнів (індивідуальні змагання, змагання між групами; дидактичні ігри тощо).
Але спочатку вчитель має розібрати способи і підходи до розв’язування і зробити відповідні записи в зошитах (конспект 13).
Щоб уявлення про спосіб дій під час додавання і віднімання мішаних чисел були більш свідомими, можна запропонувати учням спиратися на своєрідні правила додавання і віднімання мішаних чисел.
1. Щоб додати мішані числа, треба:
А) звести дробові частини цих чисел до НСЗ;
Б) окремо додати цілі, окремо дробові частини.
Якщо при додаванні дробових частин дістали скоротний дріб, то скоротіть його; якщо здобутий дріб неправильний – виділіть цілу частину цього дробу і додайте її до здобутої цілої частини.
2. Щоб виконати віднімання мішаних чисел, треба:
А) звести дробові частини цих чисел до НСЗ; якщо дробова частина зменшуваного менша від дробової частини від’ємника – перетворіть її в неправильний дріб, зменшивши на одну цілу частину;
Б) окремо відняти цілі частини, окремо дробові.
Конспект 13 Додавання і віднімання мішаних чисел 1. З однаковими знаменниками:
2. Якщо знаменники різні – зведи їх до НСЗ і див. п. 1 |
IV. Відпрацювання навичок, формування вмінь
І рівень
Усні вправи
Знайдіть значення виразу: а) 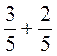 ; б)
; б) 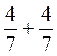 ; в)
; в) 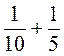 ; г)
; г) 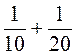 ; д)
; д) 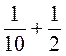 ; е)
; е) 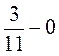 ; ж)
; ж) 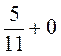 ; з)
; з) 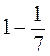 .
.
ІІ рівень
Письмові вправи
1. Знайдіть суму: а) 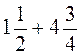 ; б)
; б) 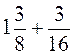 ; в)
; в) 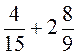 ; г)
; г) 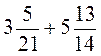 .
.
2. Знайдіть різницю: а) 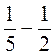 ; б)
; б) 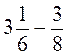 ; в)
; в) 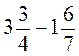 ; г)
; г) 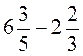 ; д)
; д) 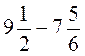 ; є)
; є) 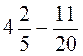 ; ж)
; ж) 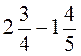 ; з)
; з) 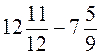 .
.
3. Знайдіть пропущені числа:

4. Розв’яжіть рівняння: а) 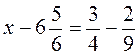 ; б)
; б) 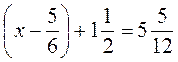 .
.
Додатково. Коли від стрічки відрізали шматок, то частина, що залишилась, мала довжину 2 м. Якою довжини була б частина, що залишилась, якщо від стрічки відрізали на 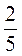 м менше? на
м менше? на 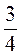 м більше?
м більше?
V. Підсумки уроку
Підставте замість квадратиків такі числа, щоб рівності були правильними:
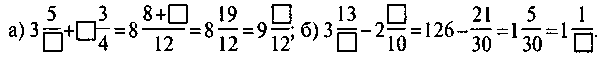
VI. Домашнє завдання
1. Обчисліть: а) 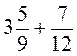 ; б)
; б) 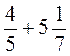 ; в)
; в) 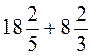 ; г)
; г) 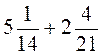 .
.
2. Знайдіть різницю 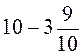 .
.
3. Знайдіть пропущені числа:
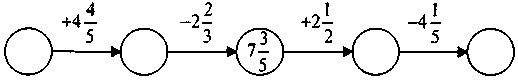
4. Розв’яжіть рівняння: а) 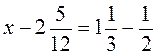 ; б)
; б) 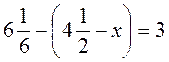 .
.
5. У двох ящиках 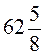 кг яблук, причому в першому ящику на
кг яблук, причому в першому ящику на 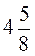 кг більше, ніж у другому. Скільки яблук у кожному ящику?
кг більше, ніж у другому. Скільки яблук у кожному ящику?
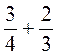 ; б)
; б) 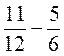 ; в)
; в) 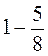 .
.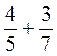 ; б)
; б) 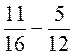 ; в)
; в) 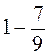 .
.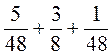 ; б)
; б) 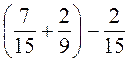 ;
;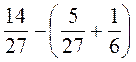 .
.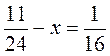 .
.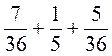 ; б)
; б) 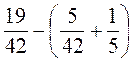 ;
;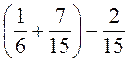 class=""/>.
class=""/>.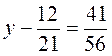 .
.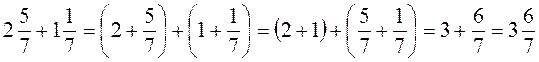 ;
;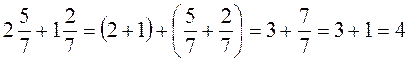 ;
;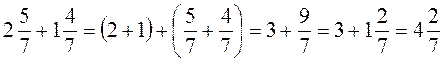 ;
;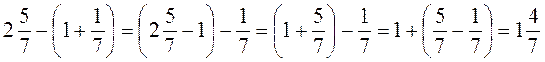 ;
;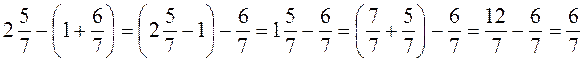 ;
;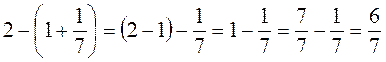 ;
;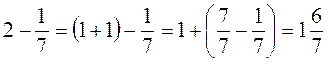 .
.