Додавання і віднімання многочленів
Розв’яжіть задачі
422. 1) Так; 2) ні.
423. 1) Ні; 2) ні; 3) так.
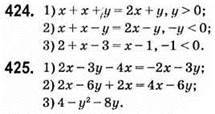
426. 1) Ні; 2) так.
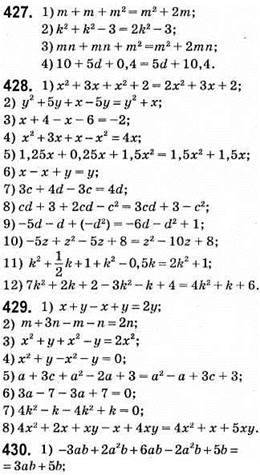
Степінь 2;
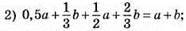степінь 1;
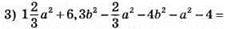
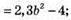степінь 2;
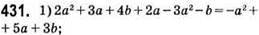
Степінь 2;
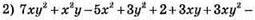
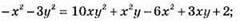степінь 3;
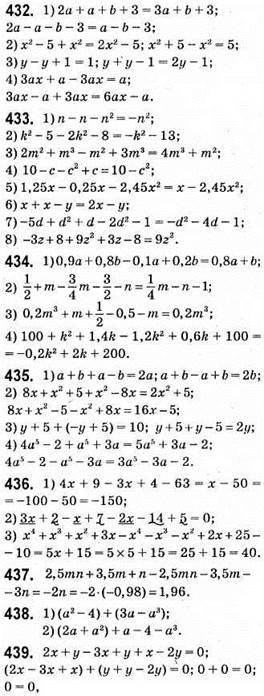
Що й треба було довести.
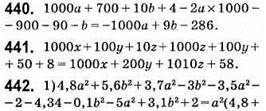
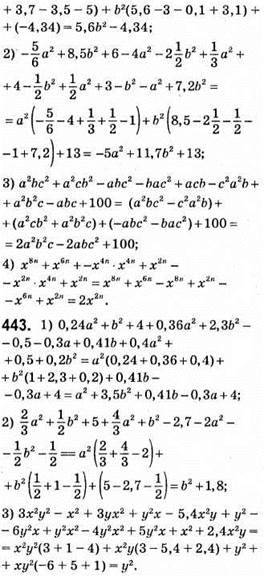
444. 1) 5×2 + 3у2 – 3 – 2х2 + у2 + 6 = 3х2 + 4у2 + 3 – другий многочлен;
2×2
2) x4 + х3 + х2 + 4х – х3 – х + 5 = x4 + х2 + 3х + 5 – многочлен;
Х4 + х2 + 3х + 5 – х3 – х + 5 = х4 – х3 + х2 + 2х + 10 – різниця;
3) у2 – 4у4 + 5 + у2 – у4 + 3 = у3 – 5у4 + y2 + 8 – многочлен;
У3 – 4у4 + 5 + y3- 5у4 + у2 + 8 = 2у3 – 9у4 + у2 + 13 – сума;
4) 4а2 + а – 2 – а2 + а – 3 = 3а2 + 2а – 5 – многочлен;
4а2 + а – 2 + 3а2 + 2а – 5 = 7а2 + 3а – 7 – сума.
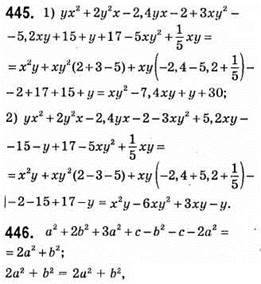
Що й треба було довести,
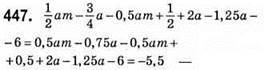
Не залежить від змінних.
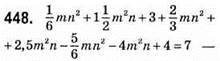не залежить від змінних.
453.
454. 46а – 3 – а + 12 = 45а + 9 = 9(5а+ 1) ділиться на 9, оскільки містить множник 9; 9(5а + 1) : 9 = 5а + 1.
455. 1) n, n + 1, n + 2 – три послідовних натуральних числа.
N + n + 1 + n + 2 = 3n + 3 = 3(n + 1);
3(n + 1) : 3 = n + 1;
2) n + n + 1 + n + 2 + n + 3 + n + 4 = 5n + 10 = 5(n + 2); 5(n + 2) : 5 = n + 2;
3) 2k, 2k + 2, 2k + 4 – три послідовних парних числа.
2k + 2k + 2 + 2k + 4 = 6k + 6 = 6(k + 1); 6(k + 1) : 6 = k + 1.
456. 2k, 2k + 2, 2k + 4, 2k + 6, 2k + 8 – п’ять послідовних парних чисел.
2k + 2k + 2 + 2k + 4 + 2k + 6 + 2k + 8 = 10k + 20 = 10(k + 2).
10(k + 2) : 10 = k + 1.
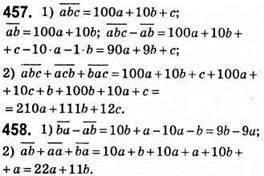
459. Це числа виду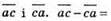 
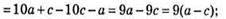
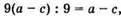значить, різниця таких чисел ділиться на 9.
460. Це числа виду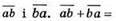 
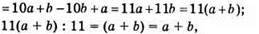
Значить, сума таких чисел ділиться на 11.
461. 5х4 + 0,3х3 + 2х + 6 – 2х3 + 7х2 – 2х + 1,7х3 +10 = 5х4 + 7х2 +16 > 0, оскільки х4 і х2 – додатні значення для будь-якого х.
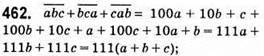
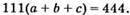
Звідки а + b + с = 4.
Можуть бути такі випадки: окрім a = 0, b = 0, с = 0:
A = 1; b = 1; c = 2; a = 1; b = 2; c = 1; a = 2; b = 1; c = 1, тобто це такі числа: 112, 121, 211.
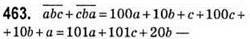
Сума таких чисел. Повинна виконуватись умова:
101а + 101с + 20b + 81b = 505;
101а+ 101b +101с = 505;
101(а + b + с) = 505.
Звідси маємо, що a + 6 + с = 5.
Можуть бути такі випадки (а ≠ 0, с ≠ 0):
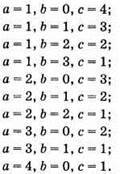
Це числа: 104, 113, 122, 131, 203, 212, 221, 302, 311, 401.
464. Це числа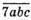 
та 
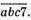Тоді повинна виконуватись рівність
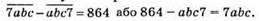
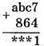тобто с = 1, маємо
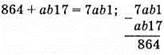
Це виконується для b = 8, а = 6. Тобто число шукане 7681.
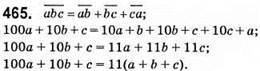
Це можливо для а = 1, b = 9, с = 8:
100 x 1 + 10 x 9 + 8 = 11 х (1 + 9 + 8); 198 = 198. Шукане число 198.
Застосуйте на практиці
466. 20% від х – 0,2х грн.
1,2х грн – прибуток через рік в банку A; 1,44х грн – прибуток через 2 роки в банку А.
20 % від 1,2х – 0,24х;
1,2x + 0,24x = 1,44x;
30 % від у – 0,3у грн
1,3у грн – прибуток через рік в банку В;
30 % від 1,3у – 0,39y;
1,3у + 0,39у = 1,69у – прибуток через 2 роки в банку В.
1,44x + 1,69у – загальний прибуток через 2 роки.
467. Нехай у першому відрі x л, тоді у другому – 2/3х л, а у третьому – 4/3x л.
Повинна виконуватися умова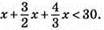 
При х = 6 маємо правильну рівність. Тобто у першому відрі 6 л, у другому
3/2 • 6 = 3 • 3 = 9 л, а у третьому 4/3 • 6 = 4 • 2 = 8 л.
Задачі для повторення
468. 
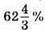від 60 км –
– довжина лінії Харківського метрополітену.
469. 25 % від 420 м – 420 • 25 : 100 = 105 (м) – глибина станції Арсенальна.
470. Сіль 2% від 20 кг морської води = 0,02 • 20 = 0,4 (кг).
Чиста вода = 20 кг – 0,4 кг = 19,6 кг.
Х кг додали солі; (20 + х) кг – маса розчину.
Сіль 4 % від (20 + х) кг = 0,04(20 + х).
Маса чистої води + маса солі = маса розчину, маємо:
19,6 + 0,04(20 + х) = 20 + х;
19,6 + 0,8 + 0,04x = 20 + x; 0,96x = 0,4;
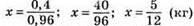солі треба додати, щоб її вміст був 4 %.
471. Сіль 2 % від 20 кг = 0,4 кг. Чиста вода = 20 – 0,4 = 19,6 (кг).
X кг додаємо води, тоді води стане (19,6 + х) кг.
(20 + х) кг – це маса розчину, а сіль 1 % від (20 + x) – 0,01(20 + х).
Маса чистої води + маса солі = маса розчину. 19,6 + х + (20 + х) • 0,01 = 20 + х; 0,01x = 0,2; x = 20 (кг) води треба додати, щоб вміст солі був 1 % .
(2 votes, average: 5.00 out of 5)
Loading...