Головна ⇒ 📌Плани-конспекти уроків по фізиці ⇒ Формула тонкої лінзи. Розв’язування задач

Формула тонкої лінзи. Розв’язування задач

2-й семестр

ЕЛЕКТРОДИНАМІКА

5. Хвильова й квантова оптика

УРОК 6/64

Тема. Формула тонкої лінзи. Розв’язування задач

Мета уроку: ознайомити учнем з формулою тонкої лінзи; навчити їх розв’язувати задачі.

Тип уроку: урок вивчення нового матеріалу.

ПЛАН УРОКУ

Контроль знань

4 хв.

1. Збиральна й розсіювальна лінзи.

2. Хід основних променів у лінзах.

3. Побудова зображення предмета в лінзах.

Вивчення нового матеріалу

31 хв.

Формула тонкої лінзи.

2. Розв’язування задач.

Закріплення вивченого матеріалу

10 хв.

1. Якісні питання.

2. Навчаємося розв’язувати задачі.

ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ

1. Формула тонкої лінзи

Розглянемо збиральну лінзу і розташуємо AB предмет на d відстані перед нею d > F. Побудуємо зображення A1B1 предмета AB, скориставшись двома вихідними із точки A променями (див. рисунок, на якому фокуси позначені F1 і F2).

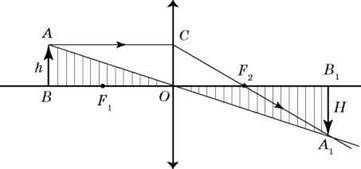
Позначимо через h висоту предмета AB, а через H – висоту зображення A1B1. З огляду на те, що OB = d, OB1 = f, з подоби трикутників

OBA і OB1A1, а також COF2 і A1B1F2 (пари подібних трикутників на рисунку виділені по-різному) одержуємо:

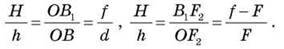
Прирівнюючи праві частини цих співвідношень, знаходимо:

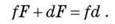
Розділивши це рівняння на Fdf, одержуємо:

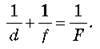
У цій формулі відстань до зображення беруть зі знаком “плюс”, якщо зображення дійсне, і зі знаком “мінус”, якщо зображення уявне. Фокусну відстань збиральної лінзи беруть зі знаком “плюс”, а розсіювальної – зі знаком “мінус”.

Використовуючи формулу тонкої лінзи, можна знайти, наприклад, відстань до зображення, якщо відомі відстань від лінзи до предмета й фокусна відстань лінзи. Виражаючи за допомогою формули лінзи f через d і F, одержимо 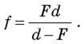Звідси також видно, що за d > F зображення дійсне (f > 0), за d < F – зображення уявне (f < 0), а якщо предмет знаходиться набагато далі від фокуса (d >> F), то f = F.

Ще раз можна нагадати учням, що заломлювальну здатність лінзи характеризує величина, названа оптичною силою лінзи. Оптична сила більше в тієї лінзи, у якої фокусна відстань менше (D = 1/F).

Формула для лінійного збільшення в загальному випадку має вигляд: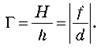

2. Розв’язування задач

1). Де на оптичній осі збиральної лінзи повинне перебувати точкове джерело світла, щоб з однієї точки простору не можна було одночасно побачити джерело і його зображення?

2). На розсіювальну лінзу падає збіжний пучок променів (див. рисунок). Після заломлення в лінзі промені перетинаються в точці, розташованій на відстані a від лінзи.

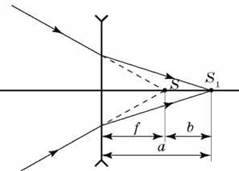
Якщо лінзу забрати, то точка перетинання променів переміститься ближче до місця, де перебувала лінза, на відстань b. Визначте фокусну відстань лінзи.

Розв’язання. Скористаємося оборотністю світлових променів. Тоді точка S1 відіграє роль джерела світла, а точка S – роль уявного зображення. З огляду на те, що f необхідно брати зі знаком “мінус”, запишемо формулу тонкої лінзи:

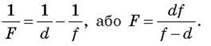
З рисунка видно, що d = a, f = a – b, отже,

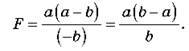
Оскільки за умовою завдання b < а, то вираз (b – а) є негативним, тому негативним є й фокусна відстань лінзи (F < 0), що відповідає розсіювальній лінзі.

3). Побудуйте зображення точки, що перебуває на головній оптичній осі розсіювальної лінзи.

4). На рисунку показані світна точка S і її зображення S1, отримане за допомогою лінзи, а також головна оптична вісь KN цієї лінзи. Визначте положення оптичного центра лінзи і її фокусів. Яка це лінза – збиральна чи розсіювальна?

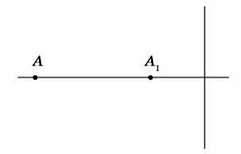
5). Дано точки A й A1 на осі лінзи невідомої форми. Визначте вид лінзи (збиральна чи розсіювальна). Побудовою знайдіть фокуси лінзи.

6). Лінза з оптичною силою D = 5 дптр дає зображення предмета, збільшене вдвічі. Визначте відстань між лінзою й предметом.

Розв’язання. Оптична сила лінзи позитивна, тобто лінза збиральна. В умові не сказано, дійсне або уявне зображення дає лінза (обидва варіанти збільшеного зображення можливі). Отже, з формули Г = lf/dl випливає, що f = 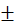Гd (лінійне збільшення Г = 2). Тоді формула тонкої лінзи набуває вигляду:

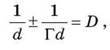
Звідки:

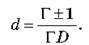
Отже, завдання має два розв’язання. Перевіривши одиниці величин і підставивши числові значення, одержуємо d1 = 0,3 м й d2 = 0,1 м.

7). Якщо предмет розташований на відстані 36 см від збиральної лінзи, то висота його зображення 10 см, а якщо на відстані 24 см – то висота його зображення 20 см. Визначте фокусну відстань лінзи й висоту предмета.

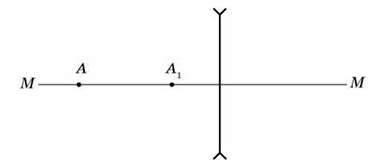
8). Визначте побудовою положення фокусів лінзи, якщо A – світна точка, A1 – її зображення. MM – головна оптична вісь лінзи.