Функція. Область визначення функції. Область значень функції
Урок № 60
Тема. Функція. Область визначення функції. Область значень функції
Мета: закріпити термінологію, відпрацювати навички роботи з поняттями функції; відпрацювати навички роботи із функцією, заданою формулою і таблично; знаходити функції аргументу, області визначення функції.
Тип уроку: засвоєння вмінь та навичок.
Хід уроку
I. Організаційний момент (традиційно)
II. Перевірка домашнього завдання
@ Оскільки основна частина домашнього завдання – опанування теорії (означення понять), то доцільно перевірку домашнього
1. Математичний диктант
1) Задайте формулою функцію, що співставляє кожному числу третій степінь цього числа [суму цього числа з числом 5].
2) Функцію задано формулою 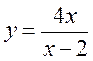
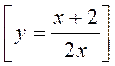 . Знайдіть її значення при значенні аргументу -2 [-1].
. Знайдіть її значення при значенні аргументу -2 [-1].
3) Функцію задано формулою у = 3х – 7 [у = 5 – 2х]. Знайдіть значення аргументу, при якому значення функції дорівнює нулю.
4) При яких значеннях змінної має зміст вираз 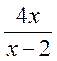
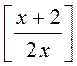 ?
?
Після перевірки виконання проводиться корекція (робота в парах).
2.
@ Основна мета роботи з випереджальним домашнім завданням на цьому уроці – підготовка до сприйняття учнями алгоритму знаходження області визначення функції, заданої формулою (вигляду у = f(х)).
Тому далі проводимо фронтальну бесіду за результатами випереджального домашнього завдання.
Запитання
1. Що називають допустимим значенням змінної у виразі? Наведіть приклад.
2. Що означає термін “область допустимих значень змінної у виразі”? Як коротко позначається?
3. Як знайти ОДЗ у виразі, який має вигляд: а) багаточлена; б) дробу, де в знаменнику число; в) дробу, знаменником якого є буквений вираз; г) цілого виразу?
4. Відшукайте ОДЗ виразів: а) х + 3; б) 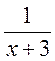 ; в)
; в) 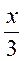 ; г) (х + 3)2; д)
; г) (х + 3)2; д) 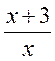 .
.
5. Назвіть аргумент і залежну змінну, якщо функцію задано формулою 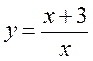 . Яких значень набуває функція при значенні аргументу -1; 2; -3? Чи можна обчислити значення функції при х = 0? Чому? Чи існує ще яке-небудь значення аргументу, при якому не можна обчислити значення виразу? Чому? Якою буде область визначення функції
. Яких значень набуває функція при значенні аргументу -1; 2; -3? Чи можна обчислити значення функції при х = 0? Чому? Чи існує ще яке-небудь значення аргументу, при якому не можна обчислити значення виразу? Чому? Якою буде область визначення функції 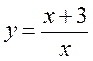 , виходячи зі сказаного вище?
, виходячи зі сказаного вище?
6. Порівняйте висновок п. 4 із п. 5. Що ви помітили? Яке припущення можна зробити на підставі цього порівняння.
III. Формулювання мети й завдань уроку
@ З роботи, виконаної на попередньому етапі уроку, учні мають зробити важливий висновок: область визначення функції може бути знайдено через ОДЗ виразу, що задає дану функціональну залежність. Тобто задання функції формулою є найбільш зручним способом задання функції саме тому, що допомагає розв’язувати задачі з незнайомими або новими для учнів об’єктами (функція, аргумент, область визначення функції) шляхом виконання знайомих учням дій (обчисленням значень буквених виразів, розв’язанням рівнянь та знаходженням ОДЗ виразу).
Отже, вчителю залишається узагальнити ці думки, і головною метою уроку можна визначити: відпрацювання навичок роботи із функцією, заданою формулою (знаходження функції аргументу й області визначення).
IV. Доповнення знань
@ Єдиним відносно новим моментом уроку є узагальнюючий логічний крок від алгоритму знаходження ОДЗ виразу (див. початок навчального року) до знаходження області визначення функції, заданої формулою як ОДЗ виразу в лівій частині цієї формули.
Звернувшись до висновків і припущення, зроблених після виконання випереджального домашнього завдання, формулюємо запитання:
– Чи існує загальне правило (алгоритм) для знаходження області визначення функції, що задано формулою?
Виконавши кілька вправ і порівнявши результати (наприклад, знайти ОДЗ виразу х+3 та знайти область визначення функції у = х + 3 і т. д.), доходимо висновку, який можна записати в конспекти учнів.
Конспект 16 | |||
Як знайти область визначення функції | |||
№ | Вид функції | Формулювання | Приклад |
1 | Багаточлен | Область визначення: х – будь-яке число | У = х2 + 3х – 2 – багаточлен; область визначення: х – будь-яке число |
2 | Цілий вираз | Область визначення: х – будь-яке число | У = (х + 3)2 – (х – 1)2 – цілий вираз; область визначення: х – будь-яке число |
3 | Дробовий вираз (знаменник – буквений вираз) | Область визначення: ті значення х, при яких знаменник не дорівнює нулю |
Х + 3 ? 0, х? -3. Область визначення: х? -3 (х – будь-яке число, окрім -3) |
V. Первинне закріплення матеріалу
Виконання усних вправ
1. Дано функцію: 1) у = х + 3; 2) у = х2 + (х – 1)2; 3) 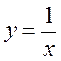 .
.
А) Яка область визначення функції? Чому?
Б) Якого значення набуває функція при значенні аргументу х = 1; х = -1?
В) Чи існує таке значення аргументу, при якому функція дорівнює 0?
VI. Застосування вмінь та навичок
Виконання письмових вправ
1. Функцію задано формулою 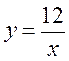 . Заповніть таблицю.
. Заповніть таблицю.
Х | -12 | -6 | 3 | -4 | 1,5 |
У | 1 | 2 | -3 | 4 | 0,5 |
2. Знайдіть область визначення функції, заданої формулою:
1) у = х2 + 1; 2) 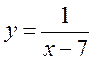 ; 3)
; 3) 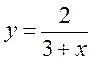 ; 4)
; 4) 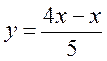 .
.
3. Функцію задано формулою у = х2 – 4х + 1. Складіть таблицю значень цієї функції з кроком 1, де -3 ? х? 4.
4. У хлопчика було 1 грн. 50 к. Він купив х календариків по 25 к за штуку. Позначивши число копійок, що залишились у хлопця, буквою у, задайте формулою залежність у від х. Яка область визначення цієї функції? А область значень функції?
5*. Додатково (логічна вправа). Знайдіть пропущене число, букву, вираз або рисунок.
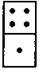
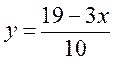
?
VII. Підсумки уроку
Які основні поняття теми “Функція” були розглянуті на уроці?
Встановіть логічний зв’язок між названими поняттями.
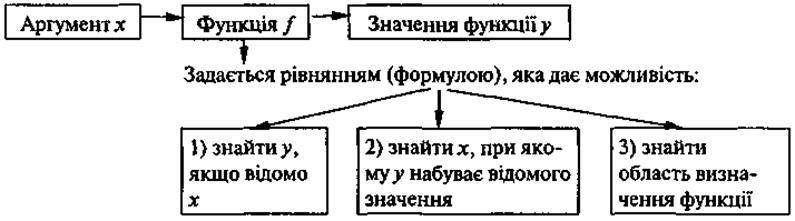
VIII. Домашнє завдання
Повторивши зміст основних теоретичних положень уроку (див. схему), виконайте вправи.
№ 1. Функцію задано формулою: 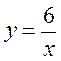 .
.
Заповніть таблицю:
Х | -12 | -6 | 24 | -24 |
У | 2 | 3 | -4 | -6 |
№ 2. (Придумайте) задайте формулою функцію, в якої область визначення:
1) будь-яке число; 2) всі числа, крім 2; 3) всі числа, крім чисел -2 та 2?
№ 3. Випереджальне домашнє завдання.
А) Розв’яжіть рівняння:
1) х2 – 2х + 1 = 0; 2) х2 – 2х = 0; 3) х2 +1 = 0; 4) |х – 3| = 0; 5) |х – 3| + 1 = 0.
Б) При яких х є правильною нерівність:
1) х2 – 2х + 1 ? 0; 2) х2 – 2х? 0; 3) х2 + 1 ? 0; 4) |х – 3| ? 0; 5) |х – 3| + 1 ? 0?
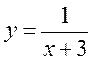 – дробовий вираз,
– дробовий вираз,