Ідеальні та реальні популяції
МЕДИЧНА БІОЛОГІЯ
Розділ 2
ПОПУЛЯЦІЙНО-ВИДОВИЙ РІВЕНЬ ОРГАНІЗАЦІЇ ЖИТТЯ ТА МІСЦЕ ЛЮДИНИ В НЬОМУ
2.1.7. Ідеальні та реальні популяції
Закон Харді – Вайнберга. Математичну залежність між частотами алелів і генотипів в ідеальній популяції встановили одночасно у 1908 р. і незалежно один від одного англійський математик Дж. Харді і німецький лікар В. Вайнберг. Ця закомірність відома як закон Харді – Вайнберга (закон генетичної рівноваги), який є основним законом популяційної генетики. Закон читається так: У вільносхрещуваній популяції
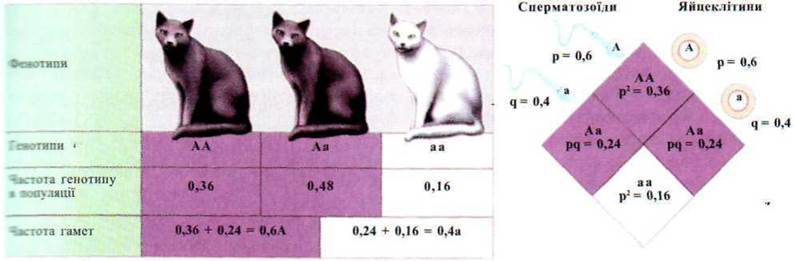
Рис. 2.8. Закон Харді – Вайнберга.
Припустимо, що в генофонді популяції, яка відповідає вищевказаним умовам, певний ген представлений алелями А і а. У популяційній генетиці частоту домінантного алеля А позначають через р, частоту рецесивного алеля а – через q. За умови, що А i a – єдині алелі гена, р+q = 1. У популяції утворюються р сперматозоїдів з алелем А, q сперматозоїдів з алелем а і р яйцеклітин з алелем А, q яйцеклітин з алелем а. При панміксії сперматозоїди (р+q) запліднюють (р+q) яйцеклітин, в результаті чого утворюються зиготи у співвідношенні, яке визначається як квадрат двочлена: (р+q) х (р+q) = (р+q)2. Тоді рівноважні частоти генотипів будуть становити: (р+q)2 = р2+2рq+q2.
Формула (р+q)2 = р2+2рq+q2 = 1 (або 100 %) є алгебраїчним виразом закону Харді – Вайнберга для двох алелів, де р – частота домінантного алеля А; д – частота рецесивного алеля а; р2 – частота домінантних гомозигот АА; 2pq – частота гетерозигот Аа; q2 – частота рецесивних гомозигот аа. У тих випадках, коли ген представлений серією алелів, формула Харді – Вайнберга має вигляд квадрата багаточлена. Для трьох алелів з частотами р, д, г, причому (p+q+r=1), рівноважна частота генотипів визначається за формулою квадрата тричлена (p+q+r)2 = p2+q2+r2+2pq+2pr+2qr. Для двох алелів гена рівноважна частота генотипів встановлюється вже в першому поколінні, для трьох і більше алелів – у наступних поколіннях, але обов’язково встановлюється.
Популяція, яка описується рівнянням Харді – Вайнберга (p+q)2, є ідеальною популяцією; вона знаходиться у стані генетичної рівноваги (генетичної стабільності). У такій популяції генофонд не змінюється з покоління в покоління, відсутня генетична мінливість і не відбувається еволюційний процес. Але еволюція на Землі триває понад 3,5 млрд. років. У природі ідеальні популяції не зустрічаються, існують реальні популяції, в яких: чисельність особин не буває нескінченно великою, панміксія не абсолютна, відбуваються мутаційний процес, природний добір, міграції. Але це не зменшує цінності закону Харді – Вайнберга. Він визначає умови генетичної стабільності вшьносхрещуваної популяції і умови, які порушують цю стабільність. Сама по собі частота генів у популяції в процесі генетичної комбінаторики (“перетасування” генів) при вільному схрещуванні не змінюється. У великих вільносхрещуваних популяціях спостерігається тенденція до відносного збереження частот алелів у ряді поколінь. Частоту генів у популяції змінюють і тим самим порушують генетичну рівновагу такі фактори, як: мутаційний процес, міграція, природний добір, дрейф генів.
З рівняння Харді – Вайнберга випливає важливий наслідок – значна частина рецесивних алелів у популяції знаходиться у гетерозиготному стані. Тому в кожному поколінні з популяції може елімінуватися лише незначна частина рецесивних алелів – ті алелі, які перейдуть у гомозиготний стан (аа), проявляться фенотипно і підпадуть під дію природного добору. Закон Харді – Вайнберга носить теоретичний характер, але має широке застосування в популяційній генетиці як основа популяційно-статистичного методу при математичному вивченні проблем еволюції. У медико-генетичних дослідженнях він без будь-яких додаткових методів дозволяє встановити частоту рецесивного патологічного алеля, частоту гетерозигот – носіїв цього алеля, генетичну структуру популяції. Для цього потрібно знати частоту рецесивних гомозигот q, тому що це єдиний генотип, який можна розпізнати за його фенотипом.