Інтерференція світла
ФІЗИКА
Частина 4
ОПТИКА. СПЕЦІАЛЬНА ТЕОРІЯ ВІДНОСНОСТІ
Розділ 12 ХВИЛЬОВІ ВЛАСТИВОСТІ СВІТЛА
12.2. Інтерференція світла
Для світлових хвиль справджується принцип суперпозиції, внаслідок чого для них характерне векторне додавання напруженостей електричних полів окремих світлових хвиль. Справедливість принципу суперпозиції зумовлена тим, що наведені в середовищі дипольні моменти прямо пропорційні напруженості зовнішнього електричного поля, тобто електричні властивості середовища мають лінійний характер. Якби співвідношення
Електромагнітне поле світлової хвилі швидко змінюється з часом. Приблизно 1015 разів за секунду напруженість електричного поля проходить через нуль, змінюючи свій напрям, і стільки ж разів досягає свого максимального значення. Зорове враження зумовлене середнім значенням квадрата електричного вектора хвилі за порівняно великий проміжок часу, а не значенням його в кожний момент. Великий проміжок часу, звичайно, треба розуміти як великий порівняно з періодом світлового коливання, який становить близько 10-15 с.
Зрозуміло, що око побачить підсилення або згасання світла тільки тоді, коли цей ефект відбуватиметься для багатьох коливань, тобто коли різниця фаз між інтерферуючими коливаннями залишається сталою. Отже, для виникнення інтерференції світлових хвиль у будь-якій точці простору потрібна сталість різниці фаз між однаково напрямленими світловими коливаннями однакової частоти, що приходять у цю точку. Такі коливання називають когерентними.
Будь-яке світне тіло складається з дуже багатьох джерел коливань: світлові хвилі породжуються окремими атомами речовини. Ми спостерігаємо завжди сумарну дію багатьох атомів. Для виникнення інтерференції від двох джерел світла потрібно, щоб у місці спостереження хвилі, які випромінюються всіма атомами одного джерела, відрізнялись за фазою на стале значення від хвиль другого джерела. Такий збіг практично неможливий, тому між променями двох різних джерел світла не може виникнути явище інтерференції. Інтерференція спостерігається тільки тоді, коли світлові промені одного джерела якимось чином (відбиванням, заломленням) були “роздвоєні” і потім знову зведені. Проте навіть у цьому разі можуть виникнути некогерентні коливання. Джерела світла, які випромінюють когерентні хвилі, називають когерентними.
Розглянемо приклад додавання двох когерентних хвиль, які поширюються від джерел S1 і S2, що містяться на відстані у1 і у2 відповідно від точки спостереження О (рис. 12.5). Коливання від джерел S1 і S2 приходять у точку О з деякою різницею фаз, яка залежить від різниці відстаней y1 і у2. Різниця фаз виникає навіть тоді, коли коливання джерел відбувається в одній фазі. Запишемо рівняння коливальних рухів, що приходять у точку О,
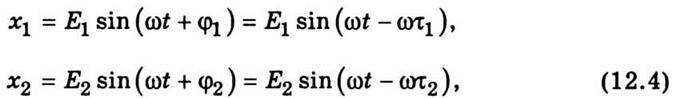
Де Е1 і Е2 – амплітуди коливань; ω – циклічна частота коливань; φ1 і φ2 – початкові фази відповідних коливань у точці спостереження; τ1 і τ2 – час поширення коливань від джерел S1 і S2 до точки спостереження. Якщо швидкість поширення світла c, то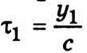 
і 
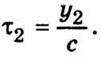Підставивши ці значення у формулу (12.4), дістанемо
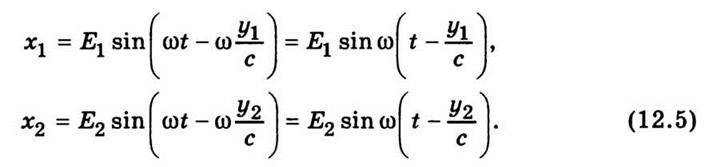
Звідси випливає, що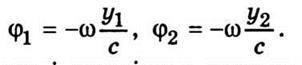 
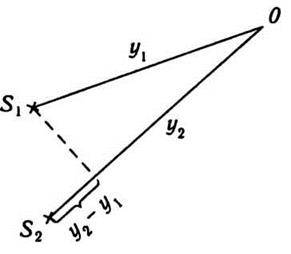
Рис. 12.5
Нас цікавитимуть фаза і амплітуда результуючого коливання, спробуємо їх знайти графічно. На рис. 12.6 зображено векторну діаграму додавання двох коливань з амплітудами відповідно E1 і Е2 та початковими фазами φ1 і φ2. Із цієї діаграми неважко дістати формулу для визначення фази результуючого коливання:
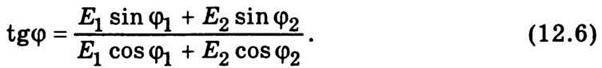
Значення амплітуди результуючого коливання дістанемо з діаграми як для сторони трикутника, що лежить проти тупого кута:
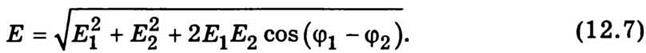
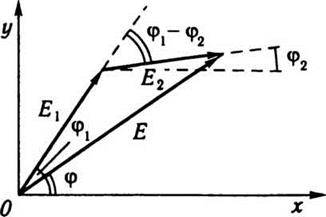
Рис. 12.6
Із формули (12.7) випливає, що амплітуда результуючого коливання визначається не тільки амплітудами коливань, що додаються, а й змінюється залежно від різниці їхніх початкових фаз. Проаналізуємо окремі випадки. Візьмемо E1 = Е2 = Е0. Виразимо різницю фаз через геометричну різницю ходу хвиль:
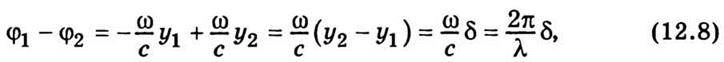
Де δ = у2 – y1 – геометрична різниця ходу хвиль (див. рис. 12.5); λ – довжина хвилі.
Розглянемо два граничних випадки:
1. Нехай різниця фаз кратна 2π: φ1 – φ2 = k2π, де k = 0, 2, … , тоді соs(k2π) = 1. Результуюча амплітуда буде
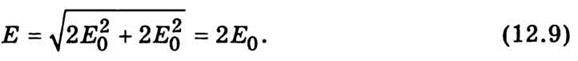
Оскільки інтенсивність світла пропорційна квадрату амплітуди електричного вектора, то в цьому разі інтенсивність результуючого коливання буде в чотири рази більшою від інтенсивності світла, яке падає від одного джерела. Встановимо зв’язок між заданою різницею фаз і різницею ходу:
Отже, інтенсивність світла внаслідок інтерференції світлових променів збільшується тоді, коли геометрична різниця ходу містить парне число півхвиль.
2. Нехай різниця фаз кратна π: φ1 – φ2 = (2k + 1)π, тоді соs(2k + 1)π = -1. Результуюча амплітуда буде
Тоді
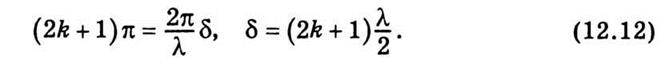
Отже, інтенсивність світла внаслідок інтерференції світлових променів дорівнює нулю, якщо геометрична різниця ходу містить непарне число півхвиль. Якщо різниця фаз φ1 – φ2 хаотично змінюється з часом з дуже великою частотою порядку 1/t (де t – тривалість збудженого стану атома), то середнє значення за часом соs(φ1 – φ2) дорівнюватиме нулю. Результуюча амплітуда двох коливань за цих умов буде
Результуюча інтенсивність від двох таких джерел світла при цьому дорівнює сумі обох інтенсивностей, які дає кожне джерело. Внаслідок того, що спостерігач не може стежити за миттєвим станом інтерференційної картини, а положення максимумів і мінімумів швидко змінюється у просторі, він сприйматиме деяку середню освітленість без максимумів і мінімумів з інтенсивністю 2I0. Джерела світла, для яких різниця фаз хаотично змінюється з часом, не можуть давати інтерференції світла з послідовними чергуваннями максимумів і мінімумів освітленості. їх називають некогерентними. Будь-які незалежні джерела світла, наприклад звичайні освітлювальні лампи, є некогерентними джерелами світла: зі збільшенням їх кількості інтенсивність результуючого освітлення ніколи не зменшується. Отже, для некогерентних джерел світла інтенсивність результуючого світла дорівнює сумі інтенсивностей падаючого світла (I = I1 + I2). Для когерентних джерел, як було показано вище, така рівність не справджується.
(1 votes, average: 5.00 out of 5)
Loading...