Головна ⇒ 📌Плани-конспекти уроків по фізиці ⇒ Кінетична і потенціальна енергія

Кінетична і потенціальна енергія

ЗАСТОСУВАННЯ ЗАКОНІВ ДИНАМІКИ

Урок № 18

Тема. Кінетична і потенціальна енергія

Мета: дати поняття про кінетичну і потенціальну енергію тіла.

Тип уроку: урок вивчення нового матеріалу.

План уроку

Контроль знань

5 хв.

1. Який зв’язок між робою та енергією?

2. Що таке механічна енергія?

3. Що є мірою зміни енергії?

Демонстрації

8 хв.

1. Залежність кінетичної енергії тіла від його маси та швидкості.

2. Енергія тіла, піднятого

на певну висоту над землею.

3. Енергія деформованої пружини

Вивчення нового матеріалу

25 хв.

1. Поняття про кінетичну енергію.

2. Залежність кінетичної енергії від маси рухомого тіла та його швидкості.

3. Теорема про кінетичну енергію.

4. Потенціальна енергія

Закріплення вивченого матеріалу

7 хв.

1. Контрольні запитання.

2. Навчаємось розв’язувати задачі

Вивчення нового матеріалу

1. Поняття про кінетичну енергію

Тіла, що рухаються, мають здатність виконувати роботу в разі зміни швидкості. Енергія, яку має тіло

внаслідок свого руху, називається кінетичною енергією.

Частина механічної енергії, зумовлена рухом тіла, називається кінетичною енергією.

Позначимо кінетичну енергію Ек.

2. Залежність кінетичної енергії від маси рухомого тіла та його швидкості

Кінетична енергія тіла, що рухається з певною швидкістю, дорівнює роботі, яку потрібно виконати, щоб надати нерухомому тілу цю швидкість. Нехай до нерухомого тіла масою m прикладено сталу силу F. Тоді Eк = А = Fs, де s – модуль переміщення. Підставляючи в цю формулу вирази F = mа і s = Кінетична і потенціальна енергія2/2a, дістанемо: кінетична енергія тіла масою m, що рухається зі швидкістю Кінетична і потенціальна енергія, виражається формулою Eк = mКінетична і потенціальна енергія2/2.

Необхідно привернути увагу учнів до того, що значення кінетичної енергії залежить від обрання системи відліку. Адже кінетична енергія тіла залежить від його швидкості, а швидкість тіла в різних системах відліку є різною. Якщо система відліку явно не вказується, зазвичай мають на увазі систему відліку, зв’язану із Землею.

3. Теорема про кінетичну енергію

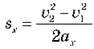Нехай тіло рухається вздовж осі x під дією сили, напрямленої вздовж тієї ж осі. Позначимо проекції швидкості тіла в початковий і кінцевий моменти Кінетична і потенціальна енергія1x і Кінетична і потенціальна енергія2x. Тоді з формул A = Fxsx, Fx = max, Кінетична і потенціальна енергія одержуємо:

Кінетична і потенціальна енергія

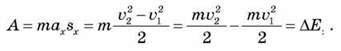
Зміна кінетичної енергії тіла дорівнює роботі, виконаній над цим тілом. Це твердження називають теоремою про кінетичну енергію.

Кінетична енергія, як і потенціальна, широко використовується людиною. За рахунок кінетичної енергії води виробляється електроенергія на гідроелектростанціях, працюють водяні млини. Кінетична енергія вітру використовується для роботи вітрових електростанцій, млинів, надає руху вітрильним суднам тощо.

4. Потенціальна енергія

На попередньому уроці учні з’ясували, що тіло має енергію або внаслідок взаємодії його з іншими тілами, або внаслідок взаємодії його частин, або внаслідок свого руху.

Частина механічної енергії, що визначається взаємним розташуванням тіл, які взаємодіють, називається потенціальною енергією.

Будемо позначати потенціальну енергію Еп.

Наприклад, якщо сила тяжіння виконує роботу під час падіння вантажу вниз, система “піднятий вантаж і Земля” має потенціальну енергію.

Позначимо зміну потенціальної енергії, 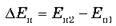Кінетична і потенціальна енергія, де індексом 1 позначено початковий стан системи, а індексом 2 – кінцевий.

Якщо під час зміни взаємного розташування тіл система виконує додатну роботу, її потенціальна енергія зменшується, а якщо система виконує від’ємну роботу, її потенціальна енергія збільшується.

Зміна потенціальної енергії? Еп і робота А, виконана системою, пов’язані співвідношенням:

?Еп = – A.

Із цієї формули випливає, що фізичний зміст має тільки зміна потенціальної енергії: вона вимірюється роботою, що її виконала система. Вибір нульового рівня потенціальної енергії визначається міркуваннями зручності для розв’язування кожної конкретної задачі.

А) Потенціальна енергія вантажу, піднятого над землею. Під час підняття вантажу масою m на висоту h виконується робота mgh, тому потенціальна енергія системи “вантаж і Земля” збільшується на mgh. Оберемо як нульовий рівень потенціальної енергії стан системи, коли вантаж перебуває на поверхні землі. Тоді Еп = mgh.

Не завжди за нульовий рівень потенціальної енергії зручно обирати рівень землі. Скажімо, перебуваючи в кімнаті, за нульовий рівень зручно обрати поверхню підлоги. Однак незалежно від того, який рівень обрано за нульовий, зміна потенціальної енергії в будь-якому конкретному досліді буде однією й тією самою.

Б) Потенціальна енергія деформованої пружини. Потенціальна енергія деформованої пружини дорівнює роботі, яку треба виконати, щоб деформувати пружину. Учні вже знають, що ця робота А = kx2/2, де k – жорсткість пружини, x – її видовження.

Отже, потенціальна енергія деформованої пружини Eп = kx2/2.

Зміна потенціальної енергії вимірюється роботою, яку може виконати система тіл у разі зміни взаємного розташування цих тіл. Якщо всі тіла системи повернулися до свого початкового положення, потенціальна енергія системи не змінилася.

Отже, потенціальну енергію можна визначити тільки для сил, робота яких під час руху по замкнутій траєкторії дорівнює нулю.

А цій умові відповідають тільки дві з розглянутих у механіці сили – сила тяжіння і сила пружності. Тому для цих сил можна використовувати поняття потенціальної енергії. Натомість робота сили тертя під час руху по замкнутій траєкторії завжди відмінна від нуля, тому для сили тертя визначити потенціальну енергію не можна.

Запитання до учнів у ході викладу нового матеріалу

1. Які з перелічених тіл мають кінетичну енергію: а) деформована пружина; б) літак, що летить; в) камінь, піднятий над землею?

2. Чи залежить значення кінетичної енергії від обрання системи відліку?

3. Після удару об стіну напрям швидкості м’яча змінився, але модуль швидкості залишився тим самим. Як змінилася кінетична енергія м’яча?

4. Тіло кинуто вертикально вгору. Яку роботу – додатну чи від’ємну – виконує сила тяжіння під час підняття тіла? під час спуску? Як змінюється кінетична енергія тіла під час підняття і спуску?

5. Як змінюється енергія пружини (збільшується чи зменшується), коли пружина повертається до недеформованого стану? Чи залежить відповідь від того, розтягнута була пружина чи стиснута?

6. Як змінюється потенціальна енергія пружини: а) коли її розтягують; б) коли її стискують; в) коли вона повертається до недеформованого стану?

7. Наведіть приклади використання потенціальної енергії тіл, піднятих над поверхнею Землі.

Задачі, розв’язувані на уроці

1. У кімнаті висотою 3 м на столі висотою 1 м лежить книга масою 1 кг. Чому дорівнює потенціальна енергія книги, якщо за нульовий рівень узято рівень столу? рівень підлоги? рівень стелі? На яку величину зміниться потенціальна енергія книги внаслідок падіння на підлогу?

2. Видовження пружини збільшилося в 3 рази. У скільки разів збільшилася потенціальна енергія пружини?

3. У якому випадку потенціальна енергія пружини є більшою: якщо пружина стиснута на 2 см чи якщо вона розтягнута на 2 см?

4. На яку висоту потрібно підняти вантаж вагою 50 Н, щоб його потенціальна енергія збільшилася на 40 Дж? На скільки потрібно опустити вантаж, щоб його потенціальна енергія зменшилася на 100 Дж?

5. Визначте потенціальну енергію пружини, стиснутої на 30 мм.

6. Як змінюються потенціальна і кінетична енергії тіла, що вільно падає; космічного корабля, який здійснює м’яку посадку?

7. За рахунок якої енергії злітає вгору наповнена гелієм повітряна кулька, що вирвалася з рук? (Відповідь: за рахунок потенціальної енергії навколишнього повітря.)

8. Яку роботу виконує під час пострілу сила тиску порохових газів, що діє на кулю? Маса кулі 9 г, швидкість вильоту з дула 600 м/c. (Відповідь: 1,6 кДж.)

9. Кулі в точці A надають певної швидкості, достатньої для досягнення точки B. По якій із гладких поверхонь (рис. 1, а, б) куля швидше досягне цієї точки? Куля під час руху не відривається від поверхні. (Відповідь: у випадку б.)

Кінетична і потенціальна енергія

Рис. 1

10. Куля масою 10 г має швидкість 400 м/c. З якою швидкістю куля продовжить свій рух після пробиття дошки товщиною 5 см, якщо середня сила опору дошки при цьому дорівнювала 12 кН?

Домашнє завдання

1. Динамометр, пружина якого розтягнута на 10 см, показує силу 100 Н. Якою є потенціальна енергія розтягнутої пружини? (Зб: № 25.16)

2. Автомобіль, рушивши з місця, на першому етапі руху набуває швидкості 40 км/год., а на другому етапі збільшує швидкість до 60 км/год. На якому етапі руху сили, що діють на автомобіль, виконують більшу сумарну роботу? У скільки разів більшу? (Зб: № 25.8)


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Потенціальна та кінетична енергія. Розв’язування задач РОЗДІЛ III МЕХАНІЧНА РОБОТА. ЕНЕРГІЯ УРОК № 9/43 Тема уроку. Потенціальна та кінетична енергія. Розв’язування задач Тип уроку: формування вмінь і навичок. Мета уроку: продовжити формувати поняття “енергія”; навчити розв’язувати типові задачі; формувати вміння аналізувати, виділяти головне. План уроку Етапи Час Прийоми і методи I. Перевірка домашнього завдання; актуалізація опорних знань 10-15 хв. Усне опитування; […]...

  2. МЕХАНІЧНА ЕНЕРГІЯ. ПОТЕНЦІАЛЬНА І КІНЕТИЧНА ЕНЕРГІЇ ТІЛА РОЗДІЛ 4 МЕХАНІЧНА РОБОТА ТА ЕНЕРГІЯ & 32. МЕХАНІЧНА ЕНЕРГІЯ. ПОТЕНЦІАЛЬНА І КІНЕТИЧНА ЕНЕРГІЇ ТІЛА Слово “енергія” ми чуємо в телевізійних репортажах, бачимо на шпальтах газет тощо. Ним можна скористатися для характеристики людей (енергійна людина), природних явищ (енергія землетрусу чи урагану), машин і механізмів (електроенергія, яку вони споживають). А що ж таке енергія з точки […]...

  3. Енергія. Потенціальна і кінетична енергія РОЗДІЛ III МЕХАНІЧНА РОБОТА. ЕНЕРГІЯ УРОК № 8/42 Тема уроку. Енергія. Потенціальна і кінетична енергія Тип уроку: засвоєння нових знань. Мета уроку: ввести поняття про фундаментальну характеристику руху й взаємодію тіл – енергію; навчити описувати фізичні явища, використовуючи закони збереження; формувати вміння учнів спостерігати, аналізувати та описувати фізичні явища. Обладнання: гиря, встановлена на стиснутій пружині; […]...

  4. Робота, енергія, потужність – ДИНАМІКА Формули й таблиці ФІЗИКА МЕХАНІКА ДИНАМІКА Робота, енергія, потужність Робота А – механічна робота постійної сили, , ; F – сила, ; S – переміщення, ; α – кут між напрямками векторів сили й переміщення Кінетична енергія Ек – кінетична енергія, ; M – маса тіла, ; υ – швидкість тіла, . Теорема про кінетичну […]...

  5. КІНЕТИЧНА ЕНЕРГІЯ Розділ 4 МЕХАНІЧНА РОБОТА ТА ЕНЕРІЯ & 53. КІНЕТИЧНА ЕНЕРГІЯ Потенціальна енергія визначає можливість тіла, яке знаходиться в певному стані, виконати роботу. Проте, якби високо ми не підняли молоток чи гирю, якщо їх стан не змінюватиметься, вони ніякої роботи не виконають. Підвішена на мотузці гиря, розтягнута або стиснута пружина можуть залишатися в такому стані тривалий […]...

  6. МЕХАНІЧНА ЕНЕРГІЯ. ПОТЕНЦІАЛЬНА ЕНЕРГІЯ Розділ 4 МЕХАНІЧНА РОБОТА ТА ЕНЕРІЯ & 52. МЕХАНІЧНА ЕНЕРГІЯ. ПОТЕНЦІАЛЬНА ЕНЕРГІЯ Енергія. Механічна енергія. Слово енергія зустрічається в різних словосполученнях: електрична енергія, сонячна енергія, теплова енергія, атомна енергія, енергія вітру та ін. Енергія, яка утворюється під час згоряння палива в двигунах автомобілів, літаків, ракет, забезпечує їх рух. Електропоїзди рухаються завдяки електричній енергії, яка виробляється […]...

  7. Механічна енергія 2-й семестр МЕХАНІЧНІ ЯВИЩА 3. Робота й енергія Урок 3/37 Тема. Механічна енергія Мета уроку: з’ясувати фізичний зміст поняття “енергія”; сформувати поняття потенціальної й кінетичної енергії. Тип уроку: комбінований урок. План уроку Контроль знань 10 хв. Самостійна робота № 16 “Механічна робота. Потужність” Демонстрації 5 хв. 1. Зміна енергії тіла під час виконання роботи. 2. […]...

  8. ВИДИ МЕХАНІЧНОЇ ЕНЕРГІЇ ТА ЇХ ЗВ’ЯЗОК З РОБОТОЮ Фізика підготовка до ЗНО комплексне видання МЕХАНІКА 3. ЗАКОНИ ЗБЕРЕЖЕННЯ В МЕХАНІЦІ 3.5. ВИДИ МЕХАНІЧНОЇ ЕНЕРГІЇ ТА ЇХ ЗВ’ЯЗОК З РОБОТОЮ Кінетична і потенціальна енергія становлять механічну енергію. Вона характеризує механічний рух. Кінетична енергія – це енергія рухомого тіла. Кінетична енергія в класичній механіці: Оскільки швидкість тіла є величиною відносною, тобто залежить від вибору системи […]...

  9. Енергія – Рукотворні системи Природознавство Природні та штучні системи в середовищі існування людини Рукотворні системи Енергія Роботу можуть здійснювати тіла, що мають енергію. Енергію виражають у джоулях, як і роботу. Види енергії Механічна енергія Буває потенціальною Та кінетичною. Потенціальну енергію має тіло, піднесене щодо Землі, будь-яке пружне деформоване тіло (пружина). Кінетичну енергію має будь-яке рухоме тіло. Що більшими є […]...

  10. Механічна енергія 5. Механіка 5.3. Закони збереження в механіці 5.3.9. Механічна енергія Механічна енергія – це фізична величина, що показує, яка робота може бути виконана силою під час переміщення тіла. Механічна енергія поділяється на два види: Потенціальна енергія – це енергія, яка визначається взаємним положенням взаємодіючих тіл або частин самого тіла. Еп = mgh. Кінетична енергія – […]...

  11. МЕХАНІЧНА ЕНЕРГІЯ ТА ЇЇ ВИДИ Розділ 4 МЕХАНІЧНА РОБОТА ТА ЕНЕРГІЯ &42. МЕХАНІЧНА ЕНЕРГІЯ ТА ЇЇ ВИДИ Для роботи двигунів, які надають руху автомобілям, тракторам, тепловозам, літакам, потрібне пальне, яке є джерелом енергії. Електродвигуни надають руху верстату завдяки електроенергії. За рахунок енергії води, яка падає з висоти, обертаються гідротурбіни, які з’єднані з електричними машинами, що виробляють електричний струм. Людині, для […]...

  12. Механічна енергія та її види Мета : з’ясувати суть поняття енергії як фізичної величини, що описує стан тіла і зміна якої визначає роботу; розпочати формування поняття потенціальної енергії; дати учням знання про кінетичну енергію рухомого тіла; показати залежність кінетичної енергії від маси тіла і його швидкості; виховувати позитивне ставлення учнів до навчально – пізнавальної діяльності. Тип уроку : комбінований. Унаочнення […]...

  13. Узагальнювальний урок 2-й семестр МЕХАНІКА 3 . Закони збереження в механіці Урок 14/58 Тема. Узагальнювальний урок Мета уроку: систематизувати й узагальнити знання учнів з теми “Закони збереження в механіці” Тип уроку: закріплення знань РЕКОМЕНДАЦІЇ ЩОДО ПРОВЕДЕННЯ УРОКУ На цьому уроці вчитель повинен узагальнити вивчений матеріал з теми “Закони збереження в механіці”. Крім того, необхідно підготувати учнів до […]...

  14. ЕНЕРГІЯ. ЗАКОН ЗБЕРЕЖЕННЯ ЕНЕРГІЇ. ВИДИ ЕНЕРГІЇ Фізика підготовка до ЗНО комплексне видання МЕХАНІКА 3. ЗАКОНИ ЗБЕРЕЖЕННЯ В МЕХАНІЦІ 3.4. ЕНЕРГІЯ. ЗАКОН ЗБЕРЕЖЕННЯ ЕНЕРГІЇ. ВИДИ ЕНЕРГІЇ Енергія – це єдина міра різних форм руху матерії. Енергія – одна з характерних властивостей матерії. На практиці механічний рух частково чи повністю перетворюється в інші форми – тепловий, електромагнітний рух. Енергія характеризує рух системи, а […]...

  15. Механічна енергія. Робота і енергія ЗАСТОСУВАННЯ ЗАКОНІВ ДИНАМІКИ Урок № 17 Тема. Механічна енергія. Робота і енергія Мета: розкрити учням сутність поняття енергії як фізичної величини, яка описує стан тіла і зміна якої визначає роботу. Тип уроку: комбінований. План уроку Контроль знань 15 хв. 1. Що таке переміщення? 2. Що таке сила? 3. Чи правильне твердження: переміщення тіла визначається тільки […]...

  16. Енергія. Види енергії Розділ 1. ПОЧИНАЄМО ВИВЧАТИ ФІЗИКУ УРОК № 8 ТЕМА. Енергія. Види енергії Мета: з’ясувати зміст поняття енергії, понять потенціальної і кінетичної енергій та закону збереження механічної енергії; вчити учнів Виділяти головне у відповідях товаришів, давати рецензії на виступи, розвивати культуру мови; спонукати до поглиблення знань. Тип уроку: урок вивчення нового матеріалу. Обладнання: нитяний маятник, тягарець […]...

  17. Закон збереження механічної енергії 2-й семестр МЕХАНІЧНІ ЯВИЩА 3. Робота й енергія Урок 4/38 Тема. Закон збереження механічної енергії Мета уроку: розкрити сутність закону збереження енергії в механічних процесах. Тип уроку: урок вивчення нового матеріалу. План уроку Контроль знань 5 хв. 1. Що таке механічна енергія? 2. Яку енергію називають потенціальною? 3. Яку енергію називають кінетичною? 4. У чому […]...

  18. Внутрішня енергія тіл. Два способи зміни внутрішньої енергії ОСНОВИ ТЕРМОДИНАМІКИ * Урок № 1 Тема. Внутрішня енергія тіл. Два способи зміни внутрішньої енергії Мета: дати молекулярно-кінетичне трактування поняття внутрішньої енергії та способів зміни внутрішньої енергії; розвивати логічне мислення, вміння аналізувати, робити висновки. Тип уроку: урок вивчення нового матеріалу. Демонстрації: залежність між об’ємом, тиском і температурою; зміна внутрішньої енергії тіла внаслідок виконання роботи. ХІД […]...

  19. Внутрішня енергія 2-й семестр ТЕПЛОВІ ЯВИЩА 4. Кількість теплоти. Теплові машини – Внутрішня енергія – Види теплообміну – Теплова рівновага. Вимірювання температури – Питома теплоємність – Енергія палива – Плавлення й кристалізація – Пароутворення й конденсація – Кипіння – Теплові двигуни Тематичне планування № з/п Тема уроку Дата проведення 1 Внутрішня енергія 2 Способи зміни внутрішньої енергії […]...

  20. Закон збереження й перетворення механічної енергії Мета : з’ясувати взаємний зв’язок потенціальної та кінетичної енергії; встановити закономірності цього зв’язку; показати учням універсальність закону збереження і перетворення механічної енергії; розвивати систематичність і послідовність мислення; виховувати розуміння важливості фізичних знань. Тип уроку : комбінований. Унаочнення : коливання пружинного маятника; маятник Максвелла; рух кульки на петлі. Обладнання : пружиний маятник, маятник Максвелла, “мертва петля”. […]...

  21. ЗАКОН ЗБЕРЕЖЕННЯ МЕХАНІЧНОЇ ЕНЕРГІЇ Розділ IV Механічна робота та енергія & 34. ЗАКОН ЗБЕРЕЖЕННЯ МЕХАНІЧНОЇ ЕНЕРГІЇ Перетворення енергії Перетворення енергії з одного виду в інший постійно відбуваються в природі і техніці. Перекриваючи ріку греблею гідроелектростанції, добиваються того, що вода піднімається на значну висоту і набуває величезної потенціальної енергії. Падаючи вниз, вода збільшує свою кінетичну енергію, за рахунок якої вона […]...

  22. Закон збереження енергії 2-й семестр МЕХАНІКА 3 . Закони збереження в механіці Урок 8/52 Тема. Закон збереження енергії Мета уроку: розкрити сутність закону збереження енергії в механічних процесах Тип уроку: вивчення нового матеріалу План уроку Контроль знань 15 хв. 1. Що таке механічна енергія? 2. Що таке кінетична енергія? 3. Теорема про кінетичну енергію. 4. Що таке потенціальна […]...

  23. Внутрішня енергія тіла та способи її змінення РОЗДІЛ IV ТЕПЛОВІ ЯВИЩА УРОК № 3/48 Тема уроку. Внутрішня енергія тіла та способи її змінення Тип уроку: комбінований. Мета уроку: ввести поняття внутрішньої енергії тіла, забезпечити засвоєння учнями двох способів вимірювання внутрішньої енергії тіла; формувати вміння спостерігати, аналізувати явища природи, визначаючи загальні ознаки. Обладнання: скляна трубка із пробкою, циліндр із поршнем (медичний шприц), мотузка. […]...

  24. ПІДСУМКИ РОЗДІЛУ IV Розділ IV Механічна робота та енергія ПІДСУМКИ РОЗДІЛУ IV – Механічна робота дорівнює добутку сили на величину переміщення: А = F ∙ s. – Потужність дорівнює відношенню роботи до часу, впродовж якого ця робота була виконана: р = . – Енергія – це можливість тіла виконати роботу. Величина енергії дорівнює найбільшій роботі, яку тіло може […]...

  25. Робота. Енергія ФІЗИКА Частина 1 МЕХАНІКА Розділ 2 ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ 2.15. Робота. Енергія Нехай тіло, на яке діє сила F, рухаючись по деякій траєкторії, проходить шлях s. При цьому під дією сили або змінюється швидкість тіла (сила надає тілу прискорення), або компенсується дія іншої сили (або сил), що протидіє руху. Дію сили F на шляху в […]...

  26. ЗАКОН ЗБЕРЕЖЕННЯ ТА ПЕРЕТВОРЕННЯ ЕНЕРГІЇ В МЕХАНІЧНИХ ПРОЦЕСАХ ТА ЙОГО ПРАКТИЧНЕ ЗАСТОСУВАННЯ Розділ 4 МЕХАНІЧНА РОБОТА ТА ЕНЕРГІЯ &43. ЗАКОН ЗБЕРЕЖЕННЯ ТА ПЕРЕТВОРЕННЯ ЕНЕРГІЇ В МЕХАНІЧНИХ ПРОЦЕСАХ ТА ЙОГО ПРАКТИЧНЕ ЗАСТОСУВАННЯ З розглянутих прикладів випливає, що всі тіла в природі мають або потенціальну, або кінетичну енергію. Але в більшості випадків тіло (наприклад, літак у польоті) має одночасно і потенціальну, і кінетичну енергії. Суму потенціальної і кінетичної енергій […]...

  27. Тематична контрольна робота “Механічна робота та енергія” Мета : перевірити якість засвоєння знань учнями з теми “Робота і енергія”; встановити рівень навчальних досягнень учнів; розвивати логічне мислення і увагу, уміння правильно розподіляти час та цінувати кожну хвилину; виховувати вимогливість до себе. Тип уроку : контролю та оцінки знань, вмінь, навичок. Обладнання : картки для тематичного оцінювання. ХІД УРОКУ Варіант 1 1. Яке […]...

  28. Закон збереження і перетворення повної механічної енергії РОЗДІЛ III МЕХАНІЧНА РОБОТА. ЕНЕРГІЯ УРОК № 10/44 Тема уроку. Закон збереження і перетворення повної механічної енергії Тип уроку: комбінований. Мета уроку: продовжити формування поняття “енергія”; розкрити суть одного із фундаментальних законів природи; навчити спостерігати та аналізувати ці явища; формувати навички самостійної роботи. обладнання: пружина, приєднаний до неї тягарець; візок, похила площина, м’яч. План уроку […]...

  29. ЗАКОН ЗБЕРЕЖЕННЯ Й ПЕРЕТВОРЕННЯ ЕНЕРГІЇ В МЕХАНІЧНИХ ПРОЦЕСАХ ТА ЙОГО ПРАКТИЧНЕ ЗАСТОСУВАННЯ Тип уроку: комбінований урок. Мета: навчити учнів описувати перетворення кінетичної енергії в потенціальну і навпаки, наводити приклади перетворення одного виду механічної енергії в інший, пояснити сутність закону збереження енергії; формувати матеріалістичний світогляд учнів. Обладнання та наочність: досліди, що ілюструють перетворення одного виду енергії в інший, портрет Ю. Р. Майера. Відеофрагмент: стрільба з лука, фрагмент мультфільму […]...

  30. Внутрішня енергія – Теплота й молекулярна фізика 6. Теплота й молекулярна фізика 6.10. Внутрішня енергія Внутрішня енергія – це енергія руху й взаємодії частинок, з яких складається тіло. Внутрішню енергію можна збільшити, виконуючи над тілом механічну роботу або теплопередачею....

  31. Закон збереження енергії в механіці Розділ IV МЕХАНІЧНА РОБОТА ТА ЕНЕРГІЯ &44. Закон збереження енергії в механіці ✓ Яку енергію називають потенціальною? ✓ Від яких фізичних величин вона залежить? ✓ Яку енергію називають кінетичною? ✓Від яких фізичних величин вона залежить? 1. У цьому параграфі ви познайомитесь з одним із найважливіших законів природи – законом збереження енергії. Цей закон має застосування […]...

  32. Контрольна робота № 5 з теми “МЕХАНІЧНА РОБОТА ТА ЕНЕРГІЯ” Тип уроку: урок контролю знань. Мета: оцінити знання, уміння та навички з вивченої теми. Обладнання та наочність: тексти контрольної роботи. Відеофрагмент:_______________________ Хід уроку I. ОРГАНІЗАЦІЙНИЙ ЕТАП II. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ III. ВИКОНАННЯ КОНТРОЛЬНОЇ РОБОТИ Приблизний варіант контрольної роботи Рівень 1 (3 бали) 1. Запишіть формулу для обчислення механічної роботи. (0,5 бала) 2. Брусок рівномірно тягнуть […]...

  33. ЕНЕРГІЯ. ПЕРЕТВОРЕННЯ ЕНЕРГІЇ Тема З РУКОТВОРНІ СИСТЕМИ § 24. ЕНЕРГІЯ. ПЕРЕТВОРЕННЯ ЕНЕРГІЇ Енергія. Ви, напевне, чули вислів “енергійна людина”. Так називають людей, здатних активно виконувати роботу. Проте не тільки люди здатні виконувати роботу. Вода, що падає з греблі, виконує роботу – обертає турбіни електростанції, вітер обертає лопаті вітряка. Тобто рухомі вода і повітря виконують роботу, отже, вони мають […]...

  34. Енергія електростатичного поля. Густина енергії ФІЗИКА Частина 3 ЕЛЕКТРИКА І МАГНЕТИЗМ Розділ 8 ЕЛЕКТРИКА 8.8. Енергія електростатичного поля. Густина енергії Припустімо, що окремі електричні заряди і заряджені тіла перебувають в однорідному ізотропному середовищі, якому не притаманні сегнетоелектричні властивості. Щоб зарядити будь-який провідник, треба виконати певну роботу проти кулонівських сил відштовхування між однойменними електричними зарядами. Ця робота витрачається на збільшення електричної […]...

  35. Енергія 5. Механіка 5.3. Закони збереження в механіці 5.3.7. Енергія Енергія – це загальна кількісна міра руху і взаємодії всіх видів матерії. Залежно від форми руху матерії розглядають різні форми енергії: механічну, внутрішню, хімічну, електромагнітну, гравітаційну, ядерну тощо....

  36. ЗАКОН ЗБЕРЕЖЕННЯ І ПЕРЕТВОРЕННЯ МЕХАНІЧНОЇ ЕНЕРГІЇ РОЗДІЛ 4 МЕХАНІЧНА РОБОТА ТА ЕНЕРГІЯ & 33. ЗАКОН ЗБЕРЕЖЕННЯ І ПЕРЕТВОРЕННЯ МЕХАНІЧНОЇ ЕНЕРГІЇ Мабуть, кожен із вас грався з м’ячиком-стрибунцем. Згадайте: м’ячик злітає вгору, падає на підлогу, відскакує від неї, знову злітає і знову падає… Коли м’ячик летить угору, швидкість його руху зменшується, потім м’ячик на мить зупиняється на певній висоті, а після цього […]...

  37. ВНУТРІШНЯ ЕНЕРГІЯ ІДЕАЛЬНОГО ГАЗУ – ВНУТРІШНЯ ЕНЕРГІЯ І ЇЇ ЗМІНА ПРИ ТЕПЛОПЕРЕДАЧІ ТА ВИКОНАННІ РОБОТИ Фізика підготовка до ЗНО комплексне видання МОЛЕКУЛЯРНА ФІЗИКА І ТЕРМОДИНАМІКА 6. ОСНОВИ ТЕРМОДИНАМІКИ 6.1. ВНУТРІШНЯ ЕНЕРГІЯ І ЇЇ ЗМІНА ПРИ ТЕПЛОПЕРЕДАЧІ ТА ВИКОНАННІ РОБОТИ 6.1.1. ВНУТРІШНЯ ЕНЕРГІЯ ІДЕАЛЬНОГО ГАЗУ Внутрішня енергія ідеального газу обумовлюється лише кінетичною енергією руху молекул; потенціальною енергією їх взаємодії можна знехтувати. Для ідеального газу масою m внутрішня енергія обчислюється за формулою […]...

  38. Тематичне оцінювання в теми “Закони збереження в механіці” 2-й семестр МЕХАНІКА 3 . Закони збереження в механіці Урок 15/59 Тема. Тематичне оцінювання в теми “Закони збереження в механіці” Мета уроку: контроль та оцінювання знань, умінь і навичок учнів з теми “Закони збереження в механіці” Тип уроку: контролю й оцінювання знань РЕКОМЕНДАЦІЇ ЩОДО ПРОВЕДЕННЯ УРОКУ Учням можна запропонувати контрольну роботу, що складається з шести […]...

  39. ВІЛЬНІ КОЛИВАННЯ МАЯТНИКІВ – ГАРМОНІЧНІ КОЛИВАННЯ Фізика підготовка до ЗНО комплексне видання КОЛИВАННЯ І ХВИЛІ. ОПТИКА 1. МЕХАНІЧНІ КОЛИВАННЯ 1.2. ГАРМОНІЧНІ КОЛИВАННЯ 1.2.2. ВІЛЬНІ КОЛИВАННЯ МАЯТНИКІВ Пружинний маятник – коливальна система, в якій коливання відбуваються під впливом сил пружності в межах пружності тіла (пружини) (рис. 3): Рис. 3 Період вільних коливань пружинного маятника: Перетворення енергії при коливаннях пружинного маятника. Енергія пружної […]...

  40. Взаємозв’язок маси та енергії 2-й семестр МЕХАНІКА 5 . Релятивістська механіка Урок 4/71 Тема. Взаємозв’язок маси та енергії Мета уроку: розглянути фізичну сутність закону взаємозв’язку маси й енергії Тип уроку: вивчення нового матеріалу План уроку Контроль знань 5 хв. 1. Відносність відстаней. 2. Відносність проміжків часу Вивчення нового матеріалу 30 хв. 1. Повна енергія тіла, що рухається вільно. 2. […]...

Ви зараз читаєте: Кінетична і потенціальна енергія
«
»