Робота. Енергія
ФІЗИКА
Частина 1 МЕХАНІКА
Розділ 2 ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ
2.15. Робота. Енергія
Нехай тіло, на яке діє сила F, рухаючись по деякій траєкторії, проходить шлях s. При цьому під дією сили або змінюється швидкість тіла (сила надає тілу прискорення), або компенсується дія іншої сили (або сил), що протидіє руху. Дію сили F на шляху в характеризують величиною, яку називають роботою.
Робота – це скалярна величина, що дорівнює добутку проекції сили на напрям переміщення РS на шляху s, який проходить точка прикладання сили,
Вираз (2.35) справедливий у тому разі, якщо проекція сили на напрям переміщення залишається незмінною. Зокрема, це відбувається тоді, коли тіло рухається прямолінійно, а стала за числовим значенням сила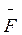 
утворює з напрямом руху сталий кут α.
Оскільки Fs = F cos α, вираз (2.35) можна записати так:
Робота – алгебраїчна величина. Якщо сила і напрям переміщення утворюють гострий кут (cos α > 0), то робота додатна. Якщо кут α тупий (cos α), робота від’ємна. При α = π/2 робота дорівнює нулю. Отже, поняття роботи в механіці істотно відрізняється
Якщо проекція сили на напрям переміщення не залишається сталою під час руху, то для визначення роботи шлях s поділяють на елементарні ділянки As так, щоб під час проходження тілом цієї ділянки силу Fs можна було вважати практично незмінною. Тоді робота на кожній елементарній ділянці буде
А робота на всьому шляху –
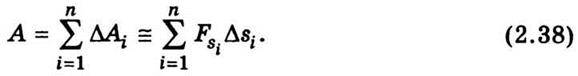
При прямуванні всіх Δsi, до нуля наближена рівність (2.38) переходить у точну:
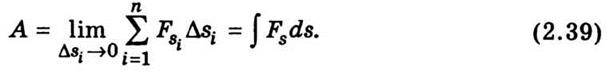
На рис. 2.8 побудовано графік залежності Fs від положення точки вздовж траєкторії (горизонтальну вісь можна назвати віссю s, а довжина відрізка вздовж цієї осі між точками s1 та s2 дорівнює довжині шляху). З рисунка видно, що робота А на шляху від точки 1 до точки 2 чисельно дорівнює площі фігури, обмеженої кривою, ординатами, що проходять через точки s1 та s2, і віссю s.
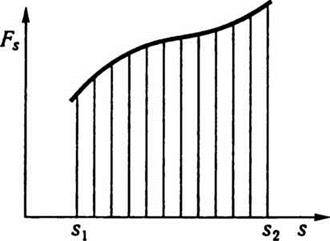
Рис. 2.8
Дослід показує, що деякі тіла здатні виконувати роботу над іншими тілами. Фізичну величину, що характеризує здатність тіла або системи тіл виконувати роботу, називають енергією. Енергія тіла може зумовлюватися, по-перше, рухом тіла з деякою швидкістю, а по-друге, знаходженням його в потенціальному полі сил. Енергію першого типу називають кінетичною, енергію другого типу – потенціальною. Отже, кінетична енергія – це енергія руху, а потенціальна – енергія положення.
Кінетична енергія матеріальної точки т, що рухається зі швидкістю υ,
Помноживши на т чисельник і знаменник виразу (2.40) і взявши до уваги, що добуток mv дорівнює імпульсу тіла р, вираз для кінетичної енергії запишемо так:
Робота, що виконується над тілом, дорівнює зміні його кінетичної енергії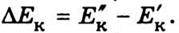 
Розглянемо матеріальну точку в потенціальному полі сил. Поставимо у відповідність кожній точці поля, що характеризується радіусом-вектором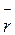 
1, певне значення деякої функції U(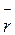), здійснивши це так. Для деякої вихідної точки О візьмемо довільне значення функції, що дорівнює U0. Щоб дістати значення U1 у деякій точці 1, додамо до U0 роботу А10, що виконується силами поля над тілом при його переміщенні з точки 1 у точку 0:
Визначена у такий спосіб функція має розмірність енергії або роботи. Оскільки робота в потенціальному полі сил не залежить від шляху, знайдене значення U1 виявляється однозначним.
Аналогічно визначимо значення U(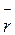) для всіх точок поля. Зокрема, значення U(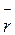) у точці 2 буде
Обчислимо різницю U1 – U2. Для цього віднімемо від (2.42) вираз (2.43) і використаємо той факт, що A20 = – A02. При цьому дістанемо
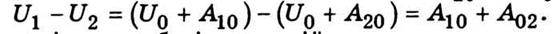
Проте сума A10 + A02 дорівнює роботі, яку здійснюють сили при переміщенні тіла з точки 1 у точку 2 по траєкторії, що проходить через точку О. Однак робота, що виконується над тілом при його переміщенні по будь-якій іншій траєкторії, буде такою самою. Тому суму A10 + A02 можна записати як А12, отже, дістанемо співвідношення
За допомогою функції U(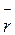) можна визначити роботу, що здійснюється над тілом силами поля на будь-якому шляху, обмеженому точками 1 і 2. Ця робота дорівнюватиме зменшенню функції U(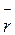) на шляху 1-2, що дає підставу трактувати фізичну величину U(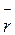) як один із різновидів механічної енергії, яку називають потенціальною.
Кожній точці потенціального поля відповідає деяке значення сили F, що діє на тіло, і потенціальної енергії тіла U. Отже, між силою і потенціальною енергією має існувати певний зв’язок. Для встановлення цього зв’язку використаємо вираз для елементарної роботи ΔА (2.37), яку здійснюють сили поля при малому переміщенні тіла Δs, що відбувається вздовж довільно обраного напряму в просторі, який позначимо літерою s.
Оскільки у цьому разі робота здійснюється за рахунок запасу потенціальної енергії, вона дорівнює зменшенню потенціальної енергії на відрізку Δs осі s:
Порівнявши (2.37) і (2.45), дістанемо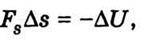 
Звідси маємо середнє значення FS на відрізку Δs. Щоб дістати значення FS у даній точці, треба виконати граничний перехід
Оскільки U змінюється не лише при переміщенні вздовж осі s, а й при переміщенні вздовж інших напрямів, то границя у формулі (2.47) є частинною похідною від U по осі s:
Для сил, що залежать лише від положення тіла, може трапитись, що робота, яку вони здійснюють над тілом, не залежить від шляху, а визначається лише початковим і кінцевим положеннями тіла у просторі. У цьому разі поле сил називають потенціальним, а самі сили – консервативними. Сили, робота яких залежить від шляху, яким тіло переходить з одного положення в інше, називають неконсервативними. Прикладом неконсервативних сил можуть бути сили тертя.
Розглянемо, як змінюються кінетична і потенціальна енергії будь-якої ізольованої системи, в якій діють лише консервативні сили. Елементарна робота консервативних сил дорівнює взятій з протилежним знаком елементарній зміні потенціальної енергії (2.45). Крім того, оскільки інші сили в консервативній системі не діють, то та сама елементарна робота дорівнює елементарній зміні кінетичної енергії. Отже,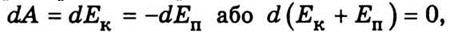 
Звідки
Ця рівність є виразом закону збереження механічної енергії, який стверджує, що повна механічна енергія консервативної системи не змінюється. Один з основних законів механіки – закон збереження енергії – можна сформулювати так: повна механічна енергія замкненої системи тіл, між якими діють лише консервативні сили, залишається сталою.
У СІ одиницею роботи є джоуль (Дж), що дорівнює роботі, яку здійснює сила в 1 Н на шляху в 1 м, а в СГС – ерг, що дорівнює роботі, яку здійснює сила в 1 дин на шляху в 1 см. Між одиницями роботи існує співвідношення:
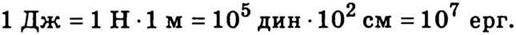
Енергія виражається в тих самих одиницях, що й робота.
(1 votes, average: 5.00 out of 5)
Loading...