Коливання вантажу на пружині. Математичний маятник
2-й семестр
МЕХАНІКА
4 . Механічні коливання й хвилі
Урок 3/62
Тема. Коливання вантажу на пружині. Математичний маятник
Мета уроку: ознайомити учнів із законами коливань пружинного та математичного маятників
Тип уроку: вивчення нового матеріалу
План уроку
Контроль знань | 5 хв. | 1. Що таке гармонічні коливання? 2. Рівняння гармонічних коливань. 3. Що таке фаза коливань? 4. Графіки гармонічних коливань |
Демонстрації | 5 хв. | 1. 2. Залежність періоду коливань вантажу на пружині від пружних властивостей пружини й маси вантажу. 3. Вільні коливання математичного маятника. 4. Залежність періоду коливань математичного маятника від його довжини |
Вивчення нового матеріалу | 25 хв. | 1. Процес коливань пружинного маятника. 2. Період коливань пружинного маятника. 3. Рівняння гармонічних коливань 4. Математичний маятник. 5. Період коливань математичного маятника |
Закріплення вивченого матеріалу | 10 хв. | 1. Тренуємося розв’язувати 2. Контрольні запитання |
ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ
1. Процес коливань пружинного маятника
Для того, щоб описати коливання (листя й колосся; повітря в органних трубах та трубах духових музичних інструментів); для розрахунку вібрації (корпусів автомашин, укріплених на ресорах; фундаментів будинків і верстатів), уведемо модель реальних коливальних систем – пружинний маятник.
O Пружинний маятник – це коливальна система, що являє собою тіло, закріплене на пружині.
Розглянемо коливання візка масою m, прикріпленого до вертикальної стіни пружиною жорсткістю k.
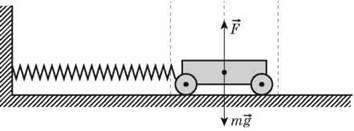
Вважатимемо, що:
1) сила тертя, яка діє на візок, дуже мала, тому можна не враховувати її. У цьому випадку коливання пружинного маятника будуть незатухаючими;
2) деформації пружини в процесі коливань тіла незначні, тому їх можна вважати пружними й застосувати закон Гука:
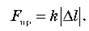
Розглянемо коливання пружинного маятника більш детально. Коли візок віддаляється від положення рівноваги на відстань А праворуч, пружина виявляється розтягнутою і на візок діє максимальна сила пружності Fnp = kA.
Потім візок починає рухатися ліворуч із прискоренням, що змінюється: подовження пружини зменшується і сила пружності (і прискорення) також зменшуються. Через чверть періоду візок повернеться в положення рівноваги. У цей момент сила пружності та прискорення дорівнюють нулю, а швидкість досягає максимального значення.
За інерцією візок продовжить рух, і виникне сила пружності, що збільшується. Вона почне гальмувати рух бруска й на відстані А від положення рівноваги візок на мить зупиниться. Від моменту початку коливань минула половина періоду.
Наступну половину періоду рух візка буде точно таким, тільки у зворотному напрямі.
Необхідно звернути увагу учнів на те, що, відповідно до закону Гука, сила пружності спрямована проти подовження пружини: сила пружності “штовхала” візок до положення рівноваги.
Отже, вільні коливання пружинного маятника зумовлені такими причинами:
1) дією на тіло сили пружності, завжди спрямованої в бік положення рівноваги;
2) інертністю коливного тіла, завдяки якій воно не зупиняється в положенні рівноваги, а продовжує рухатися в тому ж напрямі.
2. Період коливань пружинного маятника
Першу характерну ознаку коливань пружинного маятника можна встановити, поступово збільшуючи масу підвішених до пружини важків. Підвішуючи до пружини важки різної маси, ми помічаємо, що зі збільшенням маси важка період коливань вантажу збільшується. Наприклад, унаслідок збільшення маси важка в 4 рази період коливань збільшується вдвічі:
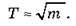
Другу характерну ознаку можна встановити, змінюючи пружини. Провівши серію вимірювань, легко виявити, що той самий вантаж швидше коливається на жорсткій пружині й повільніше – на м’якій, тобто:
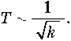
Третя особливість пружинного маятника полягає в тому, що період його коливань не залежить від прискорення вільного падіння. У цьому неважко переконатися, використовуючи метод “збільшення земного притягання” за рахунок сильного магніту, який підкладається під вантаж, що коливається.
Таким чином,
O період коливань пружинного маятника не залежить від прискорення вільного падіння й тим менший, чим менша маса вантажу й жорсткіша пружина:
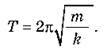
Знаючи період коливань, легко обчислити частоту й циклічну частоту коливань:
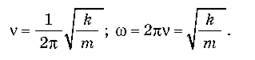
3. Рівняння гармонічних коливань
Розглянемо коливання візка з погляду динаміки. На візок під час руху діють три сили: сила реакції опори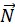 
, сила тяжіння m
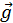і сила пружності 
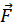Пр. Запишемо рівняння другого закону Ньютона у векторній формі:
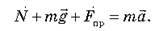
Спроектуємо це рівняння на горизонтальну й вертикальну осі:
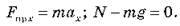
Відповідно до закону Гука:
Таким чином, маємо:
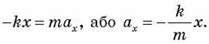
Це рівняння називають рівнянням вільних коливань пружинного маятника.
Позначимо: ?2 = k/m. Тоді рівняння руху вантажу матиме вигляд: ах = – ?2х. Рівняння такого вигляду називають диференціальними рівняннями. Розв’язком такого рівняння є функція х = Acos? t.
4. Математичний маятник
Щоб обчислити період коливань вантажу, що висить на нитці, необхідно трохи “ідеалізувати” задачу. По-перше, вважатимемо, що розміри вантажу набагато менші за довжину нитки, а нитка – нерозтяжна й невагома. По-друге, вважатимемо кут відхилення маятника досить малим (не більшим за 10-15°).
O Математичним маятником називається ідеалізована коливальна система без тертя, що складається з невагомої та нерозтяжної нитки, на якій підвішена матеріальна точка.
Розглянемо коливання математичного маятника. Для цього візьмемо невелику, але досить важку, кульку й підвісимо її на довгу нерозтяжну нитку.
Розглядаючи коливання математичного маятника, ми дійдемо висновку, що причини, які зумовлюють вільні коливання, такі ж, як і у випадку пружинного маятника (див. рис. а-д):
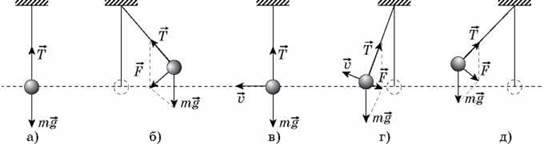
1) дія на кульку сил, рівнодійна яких завжди спрямована в бік положення рівноваги;
2) інертність коливної кульки, завдяки якій вона не зупиняється в положенні рівноваги.
5. Період коливань математичного маятника
Доведемо, що математичний маятник здійснює гармонічні коливання.
Запишемо рівняння другого закону Ньютона в проекції на вісь ОХ (див. рис.):
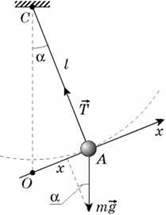
Tx + mgx = mах.
Оскільки Тх = 0, то mgx = – mgsin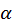
і ми дістаємо рівняння:
-mgsin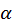 = mах, або – gsin 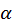= ax.
Значення sin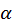 можна розрахувати з трикутника ОАС – воно дорівнює відношенню катета ОА до гіпотенузи ОС. Якщо кути малі, ОС? l, де l – довжина нитки, а ОА? х, де х – відхилення кульки від положення рівноваги. Тому sin 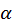= x/l.
Остаточно отримуємо:
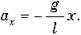
Позначивши?2 = g/l, маємо рівняння для вільних коливань математичного маятника:
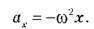
Циклічна частота коливань математичного маятника:
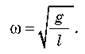
Скориставшись співвідношенням Т = 2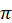
/?, знайдемо формулу для періоду коливань математичного маятника:
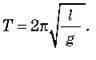
Період вільних коливань математичного маятника не залежить від його маси, а визначається лише довжиною нитки та прискоренням вільного падіння в тому місці, де знаходиться маятник.
Відомо, що в різних точках земної кулі прискорення вільного падіння різне. Воно залежить не лише від форми Землі, але й від наявності в її надрах важких (метали) або легких (газ, нафта) речовин. А отже, і період коливань маятника в різних точках буде різним. Ця властивість використовується, зокрема, під час пошуків покладів корисних копалин.
Запитання до учнів під час викладу нового матеріалу
1. Як зміниться період коливань пружинного маятника внаслідок зміни маси вантажу? жорсткості пружини?
2. Як зміниться період коливань пружинного маятника, якщо розташувати під ним магніт?
3. Як зміниться період коливань пружинного маятника, якщо збільшити амплітуду коливань.
4. За якої умови коливання математичного маятника можна вважати гармонічними?
5. Чому кулька, що коливається на довгій нитці, не зупиняється в момент проходження положення рівноваги?
6. Як зміниться період коливань математичного маятника, якщо масу вантажу збільшити? зменшити?
ЗАКРІПЛЕННЯ ВИВЧЕНОГО МАТЕРІАЛУ
1). Тренуємося розв’язувати задачі
1. Підвішений на пружині вантаж, перебуваючи в рівновазі, розтягує пружину на 10 см. Чи достатньо цих даних, щоб обчислити період коливань вантажу на пружині?
2. Коли до пружини підвісили вантаж, вона розтяглася на 20 см. Вантаж відвели вниз і відпустили. Чому дорівнює період Т коливань, що виникли?
3. Сталева кулька, підвішена до пружини, здійснює вертикальні коливання. Як зміниться період коливань, якщо до пружини підвісити мідну кульку того самого радіуса?
4. Обчисліть жорсткість пружини, якщо підвішений на ній вантаж масою 700 г здійснює 18 коливань за 21 с.
5. Яким є співвідношення довжин двох математичних маятників, якщо один з них здійснює 31 коливання, а другий за такий точно проміжок часу – 20 коливань?
2). Контрольні запитання
1. Назвіть причини коливань пружинного маятника.
2. Чи можна використати пружинний маятник для розрахунку прискорення вільного падіння?
3. Як зміниться період коливань пружинного маятника, якщо масу вантажу збільшити в 4 рази й одночасно збільшити в 4 рази жорсткість пружини?
4. Назвіть основні властивості математичного маятника. Де їх використовують?
5. Що спільного в пружинного й математичного маятників?
Що ми дізналися на уроці
– Пружинний маятник – це коливальна система, що являє собою тіло, закріплене на пружині.
– Період коливань пружинного маятника не залежить від прискорення вільного падіння й тим менший, чим менша маса вантажу й жорсткіша пружина:
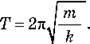
– Частота й циклічна частота коливань пружинного маятника:
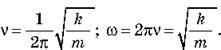
– Рівняння вільних коливань пружинного маятника:
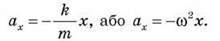
– Математичним маятником називається ідеалізована коливальна система без тертя, що складається з невагомої та нерозтяжної нитки, на якій підвішена матеріальна точка.
– Період вільних коливань математичного маятника не залежить від його маси, а визначається лише довжиною нитки та прискоренням вільного падіння в тому місці, де знаходиться маятник:
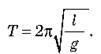
– Рівняння вільних коливань математичного маятника:
Домашнє завдання
1. П.: §§ 41, 42.
2. 36.:
Р1) – 20.7; 20.8; 20.12; 20.13, 20.14.
Р2) – 20.27; 20.28; 20.30; 20.39; 20.41.
Р3) – 20.47; 20.48; 20.49; 20.52; 20.57.
(1 votes, average: 5.00 out of 5)
Loading...