Квадрат суми та квадрат різниці двох виразів
567. (5а + 3)2 = 25а2 + 30а + 9.
568. Тотожності: 3) (12а – b)2= 144а2 – 24аb + b2.
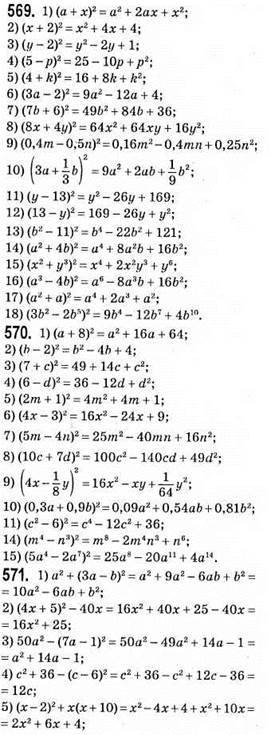
Рівняння коренів не має.
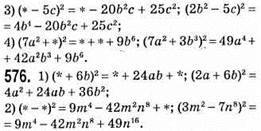
577. (a – b)2 = (b – a)2 – тотожність, бо (a – b)2 = a2 – 2ab + b2; (b – a)2 = b2 – 2ab + a2, a a2 – 2ab + b2 = b2 – 2ab + a2.
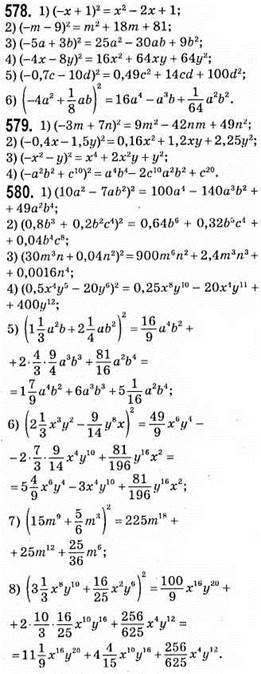
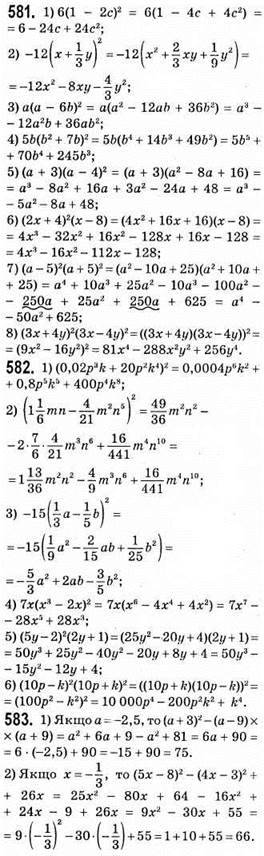
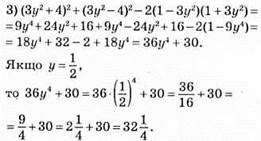
584. 1) Якщо m = -4, то 2m(m – 6)2 – m2(2m – 15) = 2m(m2 – 12m + 36) – 2m3 + 15m2 = 2m3 – 24m2 + 72m – 2m3 + 15m2 = -9m2 + 72m = -9 • (-4)2 + 72 • (-4) = -9 • 16 – 288 = -144 – 288 =
2) Якщо х = -3,5, то (2х – 5)2 – 4(x + 1)(x – 7) = 4×2 – 20х + 25 – 4(х2 – 7x + x – 7) = 4х2 – 20x + 25 – 4х2 + 28х – 4х + 28 = 4х + 53 = 4 • (-3,5) + 53 = -14 + 53 = 39.
588. х см – шукана сторона, S = х2 см2. (х + 5) см – сторона після збільшення. S = (х + 5)2 см2. За умовою (х + 5)2 – х2 = 95; х2 + 10х + 25 – х2 = 95; 10x = 95 – 25; 10х = 70; х = 70 : 10; х= 7 (см) – сторона квадрата.
589. a см – сторона даного квадрата. S = а2 см2. (а – 8) см – сторона нового квадрата. S = (a – 8)2 CM2. За умовою a2 – (a – 8)2 = 352; a2 – a2 + 16a – 64 = 352; 16a = 352 + 64; 16a = 416; a = 416 : 16; a = 26 (CM) – сторона даного квадрата.
590. Нехай х, х + 1, х + 2 – шукані числа, тоді 2(х + 2)2
2(х2 + 4х + 4) – 79 = x2 + x2 + 2х + 1; 2х2 + 8х + 8 – 79 = 2×2 + 2х + 1; 2×2 + 8х – 2×2 – 2x = 1 + 79 – 8; 6x = 72; x = 72 : 6; х = 12.
Тоді 12, 13, 14 – шукані числа.
591. Нехай х, х + 1, х + 2, х + 3 – шукані числа, тоді (х + 1)2 + (х + 3)2 – 82 = x2 + (х + 2)2; x2 + 2x + 1 + х2 + 6x + 9 – 82 = x2 + x2 + 4x + 4; 2×2 + 8х – 72 = 2×2 + 4х + 4; 2×2 + 8х – 2×2 – 4х = 72 + 4; 4х = 76; х = 76 : 4; х = 19.
Отже, 19, 20, 21, 22 – шукані числа.
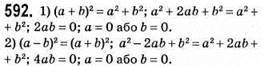
593. 1) (a + b)2 + (a – b)2 = 2(a2 + b2) – тотожність; a2 + 2ab + b2 + a2 – 2ab + b2 = 2(a2 + b2); 2a2 + 2b2 = 2a2 + 2b2 – правильна рівність.
2) (a + b)2 – (a – b)2 = 4ab – тотожність; a2 + 2ab + b2 – a2 + 2ab – b2 = 4ab; 4ab = 4ab – правильна рівність.
3) a2 + b2 = (a + b)2 – 2ab – тотожність; a2 + b2 = a2 + 2ab + b2 – 2ab; a2 + b2 = a2 + b2 – правильна рівність.
4) (a2 + b2)(c2 + d2) = (ac + db)2 + (ad – bc)2 – тотожність;
A2c2 + a2d2 + b2c2 + b2d2 = a2c2 + 2acbd + b2d2 + a2d2 – 2adbc + b2c2;
A2c2 + a2d2 + b2c2 + b2d2 = a2c2 + bd2 + a2d2 + b2c2 – правильна рівність.
594. 1) a2 + b2 = (a – b)2 + 2ab – тотожність; a2 + b2 = a2 – 2ab + b2 + 2ab; a2 + b2 = a2 + b2 – правильна рівність.
2) (a – b)2 + (ab + 1)2 = (a2 + 1)(b2 + 1) – тотожність;
A2 – 2ab + b2 + a2b2 + 2ab + 1 = a2b2 + a2 + b2 + 1;
A2 + b2 + a2b2 + 1 = a2b2 + a2 + b2 + 1 – правильна рівність.
595. 1) (x – 3)2+ (x + 3)2- 2(x – 6)(x + 6) = x2 – 6x + 9 + x2 + 6x + 9 – 2(x2 – 36) = 2×2 + 18 – 2×2 + 72 = 90. Отже, значення виразу не залежить від значення змінної х.
2) (4х3 + 5)2 + (2х3 – 1)2 – 4(5х3 + 4)(х3 + 1) = 16х6 + 40х3 + 25 + 4х6 – 4х3 + 1 – 4(5х6 + 5х3 + 4х3 + 4) = 20х6 + 36х3 + 26 – 20х6 – 20х3 – 16х3 – 16 = 10.
Отже, значення виразу не залежить від значення змінної х.
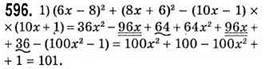
Отже, значення виразу не залежить від значення змінної х.
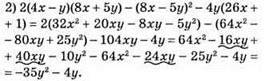
Отже, значення виразу залежить від значення змінної х.
597. 2n + 1 – непарне число. (2n + 1)2 = 4n2 + 4n + 1 – непарне число, бо 4n2 + 4n = 4(n2 + n) – парне при будь-якому значенні n, тоді 4n2 + 4n + 1 більше, ніж 4n2 + 4n, на 1, тому непарне.
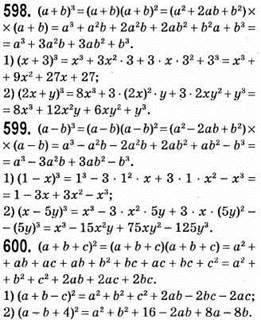
601. 1) Знайдемо площу квадрата як суму чотирьох чотирикутників: двох квадратів і двох прямокутників.
S = (а + b)2 або S = а2 + ab + ab + b2 = a2 + 2ab + b2.
Отже, (a + b)2 = a2 + 2ab + b2.
2) a2 = (a – b)2 + b2 + (a – b) • b + (a – b) • b; a2 = (a – b)2 + b2 + ab – b2 + ab – b2; a2 = (a – b)2 + 2ab – b2; a2 – 2ab + b2 = (a – b)2 або (a – b)2 = a2 – 2ab + b2.
602. 2n + 1 – непарне число. (2n + 1)2 = 4n2 + 4n + 1 = 4n(n + 1) + 1. Оскільки n і n + 1 – послідовні натуральні числа, то одне з них парне і ділиться на 2. Тому 4n(n + 1) ділиться націло на 8, тоді остача від ділення числа (4n(n + 1) + 1) на 8 дорівнює 1.
603. 4n, 4n + 1, 4n + 2, 4n + 3 – чотири послідовних натуральних числа. 4n кратне 4, тому квадрат цього числа ділиться націло на 4.
(4n + 1)2 = 16n2 + 8n + 1= 4(4n2 + 2n) + 1. Остача від ділення на 4 дорівнює 1.
(4n + 2)2 = 16n2 + 16n + 4 = 4(4n2 + 4n + 1). Остача від ділення на 4 дорівнює 0.
(4n + 3)2 = 16n2 + 24n + 9 = 16n2 + 24n + 8 + 1 = 4(4n2 + 6n + 2) + 1. Остача від ділення на 4 дорівнює 1.
Отже, остача від ділення квадрата натурального числа на 4 дорівнює 0 або 1.
604. х2 + (х + 1)2 – 2х(х + 1) = х2 + х2 + 2х + 1 – 2х2 – 2х = 1. Отже, різниця не залежить від вибору чисел.
605. 16n + 4 – дане натуральне число. (16n + 4)2 = 256n2 + 128n + 16 = 16(16n2 + 8 + 1); ділиться наділо на 16, бо 16 ділиться на 16.
606. 25n + 5 – дане число. (25n + 5)2 = 625n2 + 250n + 25 = 25(25n2 + 10n + 1) – кратне 25, бо 25 кратне 25.
607. 9n + 5 – дане натуральне число. (9n + 5)2 = 81n2 + 90n + 25 = 81n2 + 90n + 18 + 7 = 9(9n2 + 10n + 2) + 7. Остача від ділення квадрата даного числа на 9 дорівнює 7.
608. 11n + 6 – дане число.
Його квадрат (11n + 6)2 = 121n2 + 132n + 36 = 121n2 + 132n + 33 + 3 = 11(11n2 + 12n + 3) + 3.
Остача від ділення квадрата числа на 11 дорівнює 3.
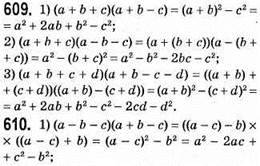
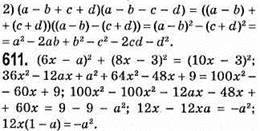
При а = 1 рівняння має вигляд 0 • х = -1 і не має коренів.
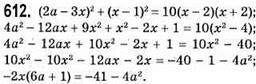
Якщо 6а + 1 = 0, тобто 6а = -1; а = -1/6, рівняння має вигляд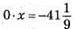 
і не має коренів.
613. (2n + 1)2 + (2n2 + 2n)2 = (2n2 + 2n + 1)2 – тотожність;
4n2 + 4n + 1 + 4n4 + 8n3 + 4n2 = 4n4 + 4n2 + 1 + 8n3 + 4n2 + 4n;
8n2 + 4n4 + 8n3 + 4n + 1 = 4n4 + 8n2 + 8n3 + 4n + 1 – рівність правильна.
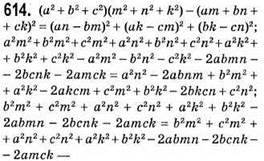
Рівність правильна.
615. Нехай x – 2, x – 1, x, x + 1, x + 2 – послідовні натуральні числа (х > 2).
Тоді (х – 2)2 + (х – 1)2 + х2 + (х + 1)2 + (х + 2)2 = х2 – 4х + 4 + х2 – 2х + 1 + х2 + х2 + 2х + 1 + х2 + 4х + 4 = 5х2 + 10 = 5(х2 + 2).
Щоб це число можна було подати у вигляді квадрата натурального числа, необхідно, щоб х2 + 2 було кратне 5.
Але х2 + 2 може закінчуватися цифрами: 3, 6, 7, 8, 1, тому не може бути кратним 5.
Отже, число 5(х2 + 2) не можна подати у вигляді квадрата натурального числа.
616. 1) 3600 • 0,25 = 900 т цукру одержимо з 3600 т буряків;
2) 900 : 0,18 = 5000 т цукрової тростини необхідно для того, щоб отримати 900 т цукру.
617. Нехай апельсинів було х ящиків, тоді бананів (80 – х) ящиків. Апельсинів привезли 10 кг, а бананів 8(80 – х) кг.
Тоді 10 + 8(80 – х) = 740; 10х + 640 – 8х = 740; 2х = 740 – 640; 2x = 100; х = 100 : 2; х = 50 ящиків апельсинів привезли до магазину; 80 – 50 = 30 ящиків бананів привезли до магазину.
50 • 10 = 500 кг апельсинів привезли до магазину;
30 – 8 = 240 кг бананів привезли до магазину.
618. 
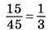– ймовірність витягнути білу кульку з першої коробки.
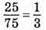– ймовірність витягнути білу кульку з другої коробки.
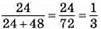– ймовірність витягнути білу кульку з третьої коробки.
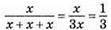– ймовірність витягнути білу кульку з четвертої коробки.
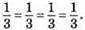
Отже, ймовірність навмання витягнути білу кульку для всіх коробок однакова.
619. 1) Найменше значення виразу х2 дорівнює 0 при х = 0.
2) Найменше значення виразу х2- 16 дорівнює -16 при х = 0.
3) Найменше значення виразу (х + 4)2 + 20 дорівнює 20 при х = -4.
620. 1) Найбільше значення виразу – х2 дорівнює 0 при х =0.
2) Найбільше значення виразу – х2 + 4 дорівнює 4 при х = 0.
3) Найбільше значення виразу 12 – (х – 1)2 дорівнює 12 при х = 1.
621. 1) (х – 1)2 + (х + 1)2 = -10. Ця рівність не виконується при жодному значенні х.
2) (х – 1)2 + (х + 1)2 = 0; таких значених немає, при яких виконується ця рівність.
3) (х2 – 1)2 + (х + 1)2 = 0; рівність виконується при х = -1.
622. 1) (х + 2)2 + (у – 6)2 = -1; таких значень х і у немає, при яких виконується рівність.
2) (х + 2)2 + (у – 6)2 = 0. Ця рівність виконується при х = -2 і у = 6.
(1 votes, average: 5.00 out of 5)
Loading...