Головна ⇒ 📌Довідник с фізики ⇒ Квантування гідрогеноподібних йонів

Квантування гідрогеноподібних йонів

ФІЗИКА

Частина 5 АТОМНА ФІЗИКА

Розділ 15 БУДОВА АТОМА

15.5. Квантування гідрогеноподібних йонів

Гідрогеноподібні йони – це такі іони, навколо ядер яких обертається лише один електрон. До них належать йонізований гелій, двічі йонізований літій, тричі йонізований берилій, чотири рази іонізований бор і т. д. Розглянемо, з погляду теорії Бора, походження спектрів цих атомів, що складаються з позитивно зарядженого ядра і одного електрона, який обертається навколо ядра. Під впливом притягання ядра, яке обернено пропорційне квадрату

відстані між ядром і електроном, електрон має рухатися по еліпсу, в одному з фокусів якого розміщене ядро. Проте на противагу класичній електродинаміці електрон при цьому не повинен випромінювати світло. На рис. 15.6 зображено такі орбіти: К(n = 1), L(n = 2), М (n = 3), N (n = 4), Q(n = 5). У першому наближенні орбіти можна вважати коловими. Коли електрон переходить із зовнішньої орбіти на внутрішню, наприклад з 4-ї на 2-гу або з 3-ї на 1-шу, то сила притягання до ядра виконує роботу так само, як сила тяжіння Землі при падінні тіла на неї. Частина цієї роботи йде на збільшення кінетичної енергії електрона, тому його швидкість на внутрішній орбіті

більша, ніж на зовнішній.

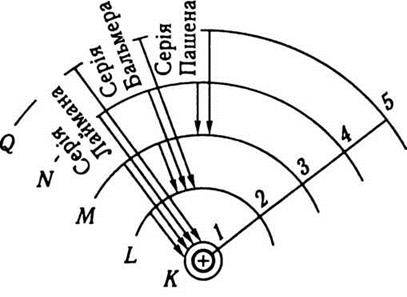
Рис. 15.6

Решта енергії перетвориться в енергію випромінювання. Якщо електрон досягне найближчої до ядра орбіти, то він уже не зможе більше наближатись до ядра і, отже, не зможе випромінювати світло, поки знову не буде переведений на одну із зовнішніх орбіт. Це відбувається тільки при поглинанні достатньої кількості енергії ззовні. Найближча до ядра внутрішня орбіта відповідає рівноважному основному або нормальному стану атома; всі інші орбіти відповідають збудженим станам атома.

Розглянемо електрон, що рухається в полі атомного ядра із зарядом Ze. Якщо Z = 1, то така система відповідає атому гідрогену, якщо Z > 1 – гідрогеноподібному йону. Для спрощення розрахунків вважатимемо, що рух електрона відбувається по коловій орбіті. При цьому на електрон діятиме доцентрова сила, роль якої відіграє сила кулонівської взаємодії між електроном і ядром. Тоді в системі СГСЕ

Де m – маса електрона; е – його заряд; υ – швидкість руху по орбіті радіуса rn.

Одночасно з рівністю (15.12) має виконуватись умова стаціонарності орбіти (15.11). Розв’язавши систему рівнянь (15.11) і (15.12), можна визначити швидкість руху електрона по стаціонарній орбіті

І її радіус

Для певного хімічного елемента всі величини справа – сталі, змінюватись може лише n. Отже, радіус стаціонарної орбіти змінюється стрибкоподібно, оскільки n = 1, 2, 3,…. Із формули (15.14) випливає, що радіус найближчої до ядра орбіти (n = 1) в атомі гідрогену (z = 1) буде

Підставляючи в (15.15) значення h, m і е, знайдемо, що радіус першої можливої орбіти в атомі дорівнює 0,529 ∙ 10-10 м. Це значення відповідає розмірам атома гідрогену, які знайдені з кінетичної теорії газів.

Згідно з теорією Бора енергія, що випромінюється або поглинається атомом, дорівнює різниці між енергіями стаціонарних станів атома. Тому для перевірки теорії Бора доцільно було б порівняти розраховані значення різниці енергій стаціонарних станів з енергією, що випромінюється атомами.

Енергія атома гідрогену або гідрогеноподібного йона складається з потенціальної енергії взаємодії між ядром та електроном і кінетичної енергії електрона, який рухається навколо ядра.

Потенціальну енергію можна знайти, виходячи з того, що робота електричної сили притягання при переміщенні електрона з орбіти радіуса rn на нескінченність дорівнює його потенціальній енергії En. Справді,

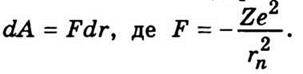
Тоді

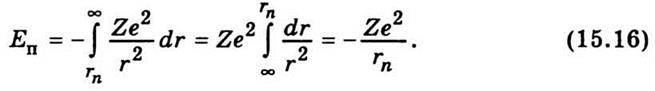
Ураховуючи співвідношення (15.12), дістанемо вираз для кінетичної енергії електрона

Повна енергія атома буде

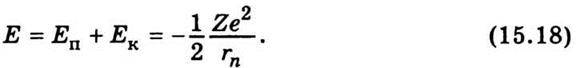
Або, враховуючи значення rn з (15.14), маємо

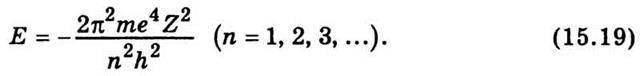
Знак мінус у співвідношенні (15.19) зумовлений тим, що потенціальна енергія двох зарядів, які нескінченно віддалені один від одного, дорівнює нулю. При наближенні зарядів один до одного потенціальна енергія зменшується, причому вона зменшується швидше, ніж зростає кінетична енергія. Тому обчислене значення повної енергії Е буде від’ємним. Оскільки повна енергія атома є величиною від’ємною, то більшому значенню повної енергії відповідає менше її абсолютне значення, тобто зі збільшенням радіуса орбіти (збільшенням квантового числа ті) зростатиме енергія атома.

Для атома гідрогену (Z = 1) співвідношення (15.19) набирає вигляду

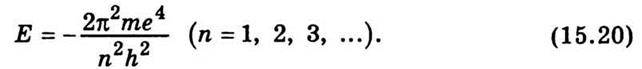
Згідно з теорією Бора атоми гідрогену випромінюватимуть кванти світла, якщо здійснюватиметься перехід від стаціонарних станів з більшою енергією в стаціонарні стани, яким відповідають менші значення енергії. При цьому частота випромінювання світла визначається співвідношенням

Де Еn – енергія початкового стаціонарного стану; Еl – енергія кінцевого стаціонарного стану.

Підставляючи в (15.21) вираз (15.20), який визначає енергію стаціонарного стану, дістанемо

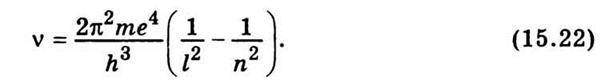
Знайдений результат ідентичний узагальненій формулі Бальмера (15.9), причому стала Рідберга визначається співвідношенням

Якщо підставити в цей вираз значення універсальних констант, то можна дістати значення сталої Рідберга, яке з високим ступенем точності збігається з її експериментальним значенням.

У теорії Бора стає зрозумілою природа спектральних серій. Спектральні серії – це монохроматичні випромінювання, що виникають унаслідок переходу атома в певний стан (з певним значенням квантового числа) з усіх можливих збуджених станів. Так, серія Лаймана відповідає переходам із збуджених станів з квантовими числами n > 1 у нормальний, що характеризується квантовим числом l = 1. Оскільки в цьому разі всі переходи відбуваються на найнижчий рівень, то різниця термів, що відповідає цьому рівню і рівню, з якого відбувається перехід, буде відносно великою, тому й випромінені кванти матимуть велику частоту. Як зазначалося, серія Лаймана належить до ультрафіолетової частини спектра. Серія Бальмера, що міститься у видимій частині спектра атома гідрогену, утворюється внаслідок переходів електрона на орбіту, для якої l = 2, з орбіт з квантовими числами n > 2. Аналогічно можна пояснити походження інших серій У спектрі атома гідрогену. При цьому відповідні розрахунки приводять до результатів, що добре узгоджуються з експериментом.

Отже, теорія Бора пояснила спектральний склад і механізм виникнення спектральних ліній атома гідрогену і гідрогеноподібних йонів, розкрила фізичний зміст чисел l і n. Проте, виходячи з неї, неможливо побудувати теорію атома гелію, який у періодичній таблиці Д. І. Менделєєва розташований безпосередньо за гідрогеном. Це була перша велика невдача, якої зазнала теорія Бора.

Для визначення енергії стаціонарних станів Н. Бор користувався звичайними засобами класичної механіки, але це при квантовому змісті вихідних постулатів надавало теорії Бора половинчастого характеру, позбавляло її внутрішньої послідовності.

Пізніше, в 20-х роках, Е. Шредінгер, В. Гейзенберг, М. Борн, П. Дірак розвинули більш точну квантову теорію, створили квантову механіку.