МЕХАНІЧНА ЕНЕРГІЯ. ПОТЕНЦІАЛЬНА ЕНЕРГІЯ
Розділ 4 МЕХАНІЧНА РОБОТА ТА ЕНЕРІЯ
& 52. МЕХАНІЧНА ЕНЕРГІЯ. ПОТЕНЦІАЛЬНА ЕНЕРГІЯ
Енергія. Механічна енергія. Слово енергія зустрічається в різних словосполученнях: електрична енергія, сонячна енергія, теплова енергія, атомна енергія, енергія вітру та ін. Енергія, яка утворюється під час згоряння палива в двигунах автомобілів, літаків, ракет, забезпечує їх рух. Електропоїзди рухаються завдяки електричній енергії, яка виробляється на атомних, теплових або гідроелектростанціях. Електрична енергія забезпечує виконання роботи різноманітними
Грецькою мовою слово енергія означає дію, діяльність. Вчені назвали цим словом фізичну величину, щоб кількісно характеризувати рухи і взаємодії в усіх їх проявах. Рух матерії, тобто зміни в навколишньому світі, як ви знаєте, проявляється через механічні, теплові, електричні, світлові та інші явища. Залежно від явищ розрізняють різні форми енергії.
Особливості руху тіл і частинок, з яких вони складаються, визначаються їх взаємодією.
Потенціальна енергія тіла, на яке діє сила тяжіння. Вам мабуть доводилося забивати гвіздки. Щоб забити гвіздок, ми піднімаємо молоток і потім опускаємо його на шляпку гвіздка. Сила, з якою молоток діє на гвіздок, надає йому руху і виконує роботу з його забивання (мал. 4.6). Замість молотка можна використати гирю, підвішену на нитці. Якщо під нею поставити дошку із вколотим гвіздком, то гиря, падаючи, заб’є його в дошку (мал.4.7).
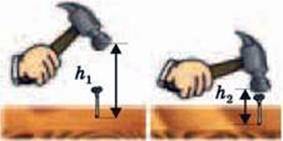
Мал. 4.6
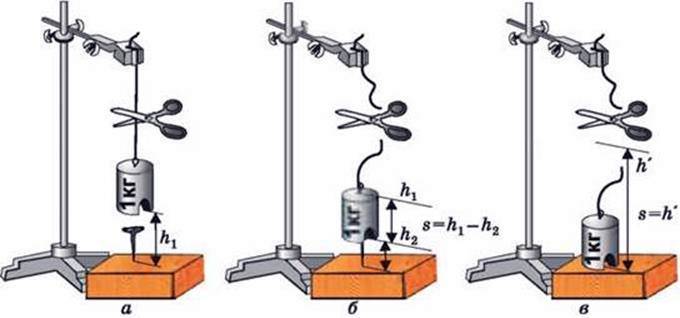
Мал. 4.7
Піднятий на деяку висоту молоток або гиря здатні виконати роботу. Чому виконується ця робота? Від чого залежить її результат? Проведемо дослід із гирею. Нехай піднята над дошкою гиря перебуває в стані спокою, що визначається висотою h1 та масою m (мал. 4.7, а) Переріжемо нитку. Під дією сили тяжіння гиря падає, її висота зменшується, а швидкість зростає. Після удару об гвіздок її стан визначається новою висотою h2 – відстань від голівки гвіздка до дошки (мал. 4.7, б). Падаюча гиря пройшла шлях s = h1 – h2; гвіздок увійшов у дошку. Стан гирі змінився унаслідок роботи, виконаної силою тяжіння. Визначимо цю роботу:
А = Fs = Fтяж (h1 – h2) = Fтяж h1 – Fтяж h2.
Повторимо дослід, піднявши гирю вище – на висоту h’. Тепер робота, виконана силою тяжіння з переміщення гирі, більша, і гвіздок увійде в дошку глибше. Піднята вище гиря здатна виконати більшу роботу. Якщо внаслідок падіння гирі гвіздок повністю увійде в дошку, то пройдений шлях і виконана робота визначатимуться лише висотою підняття гирі над дошкою: А = Fs = Fтяжh ‘ (мал. 4.7, в) . Сила тяжіння, що діє на гирю, і висота підняття гирі над Землею визначають її здатність виконати роботу.
Величину, що визначає здатність тіла, піднятого на певну висоту над Землею, виконати ту чи іншу роботу, називають потенціальною * енергією тіла, піднятого над Землею, і позначають Еп.
* Від лат. потенціал – можливість.
Сила тяжіння біля поверхні Землі, як знаєте, залежить від маси тіла: Fтяжm = mg. Якщо тіло падає на поверхню Землі, то його висота h2 дорівнюватиме 0. Пройдений тілом шлях дорівнює висоті його підняття h. Робота, виконана силою тяжіння, у цьому випадку становить А = Еп = Fтяжh = mgh. Тому для тіла, піднятого над Землею, потенціальну енергію визначають за формулою
Еп = mgh.
Потенціальна енергія тіла, піднятого над Землею, залежить від висоти (взаємного розташування тіла і Землі) та сили тяжіння.
Одиницею енергії, як і роботи, у СІ є джоуль. Енергія в 1 Дж – це енергія, наприклад, тягарця масою 102 г, піднятого на висоту 1 м.
Потенціальна енергія пружно-деформованого тіла. Прикріпимо до гачка брусочка, що лежить на столі, пружину і закріпимо її вільний кінець. Відтягнемо його так, щоб пружина видовжилась, а потім відпустимо. Скорочуючись, пружина переміщує брусок на певну відстань, діючи на нього силою пружності, і виконує роботу (мал. 4.8).
Зігнутий лук з натягнутою тятивою здатен послати стрілу на значну відстань і вразити нею ціль (мал. 4.9). Закручені гумові нитки надають руху моделям літаків (мал. 4.10), кораблів, автомобілів, виготовленим юними техніками. Хід механічного годинника забезпечує пружина. В усіх цих випадках роботу виконує сила пружності. Отже, пружно-деформовані тіла теж здатні виконувати роботу, тобто вони мають енергію.
Енергія, яку мають тіла внаслідок пружної деформації, називають потенціальною енергією пружно-деформованого тіла.
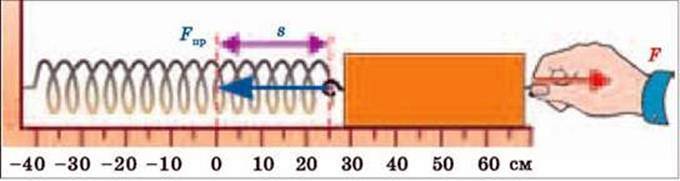
Мал. 4.8
Мал. 4.9
Мал. 4.10
Від чого залежить енергія тіл, що виникає внаслідок їх пружної деформації? Неважко переконатися, що чим більша деформація (розтяг, стиснення та ін.) тіла, тим більша сила пружності виникає в ньому і тим більшу роботу воно здатне виконати. Щоб якомога далі послати стрілу, слід сильніше зігнути лук, натягуючи його тятиву. Більш розтягнута пружина перемістить брусочок на більшу відстань і діятиме на нього з більшою силою. Отже, енергія пружно-деформованого тіла залежить від його деформації.
Чому пружно-деформовані тіла мають енергію? Коли тіло підняте над Землею, його потенціальна енергія залежить від взаємного розташування тіла і Землі (висоти над Землею). У випадку деформації пружних тіл їх стан і відповідно енергія, яка його характеризує, теж визначаються взаємним розміщенням, але вже не тіл, а лише окремих їх частинок.
Потенціальною енергією називають енергію тіл, яка залежить або від їх взаємного розташування (координат), або від взаємного розташування частинок одного й того самого тіла.
Як можна визначити потенціальну енергію пружно-деформованого тіла? Розглянемо найпростіший випадок. Ви розтягнули пружину динамометра з силою 4 Н. Яку роботу може виконати пружина динамометра, скорочуючись до позначки 0? Для визначення роботи необхідно силу помножити на шлях: А = Fs. Шлях, пройдений гачком пружини динамометра, дорівнюватиме розтягу пружини: s = Δl (мал. 4.8). Сила пружності під час скорочення пружини змінюється від 4 Н до 0. Але ми знаємо, що ця сила прямо пропорційна видовженню. Тому можна легко знайти середнє значення сили пружності: Fс = 
. Отже, A = Fcs = FcΔl = Δl. Пригадайте, значення сили пружності, що виникає під час пружних деформацій, визначається за законом Гука: F = kΔl (k – коефіцієнт жорсткості пружини). Підставивши визначену за законом Гука силу у попередню формулу, отримаємо
A = FпрΔl =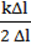 
= 
.
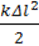Оскільки пружина динамометра, скоротившись до позначки 0, стає недеформованою й не може у цьому стані виконувати роботу, її енергію можна прийняти такою, що дорівнює 0. Тому робота, виконана пружиною під час стискання, дорівнює її енергії:
Eп = A =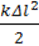
ЗАПИТАННЯ ТА ЗАВДАННЯ
1. Яку енергію називають потенціальною?
2. Як визначити потенціальну енергію тіла, піднятого на деяку висоту над поверхнею Землі?
3. Від чого і як залежить потенціальна енергія пружно-деформованого тіла?
4. Доведіть, що підняте на деяку висоту над поверхнею Землі тіло має потенціальну енергію.
5. Доведіть, що деформоване пружне тіло має потенціальну енергію.
6. Який зв’язок між роботою, виконаною над тілом, і його енергією?
7. Від чого залежить числове значення потенціальної енергії тіла? Чи можна однозначно стверджувати, що енергія тіла, піднятого над Землею, дорівнює 10 Дж? Що ще слід зазначати, вказуючи числове значення енергії?
8. Яка форма механічної енергії у заведеної пружини годинника?
9. Під час кладки стіни другого поверху будинку на перекриття першого поверху з висоти 1,5 м впала цеглина. Перекриття розташоване на висоті 4 м над поверхнею Землі. Маса цеглини 4 кг. Визначте:
А) яку роботу виконала сила тяжіння, під дією якої падала цеглина; б) якою була початкова потенціальна енергія цеглини відносно перекриття і відносно поверхні Землі; в) якою стала енергія цеглини після падіння (відносно перекриття і відносно поверхні Землі; г) чи однакову роботу виконала сила тяжіння під час падіння цеглини за оцінками муляра, який робить кладку стіни на цьому поверсі, і спостерігача, який знаходиться на поверхні Землі?
10. Кран підняв на висоту 10 м вантаж масою 1,5 т. Яку роботу виконав двигун крана з піднімання вантажу? На скільки і як (збільшилася, чи зменшилася) енергія вантажу?
(1 votes, average: 5.00 out of 5)
Loading...