МЕХАНІЧНА РОБОТА. ПОТУЖНІСТЬ
Розділ IV Механічна робота та енергія
& 32. МЕХАНІЧНА РОБОТА. ПОТУЖНІСТЬ
Механічна робота
Механічною роботою називають переміщення тіла під дією сили. Роботу можна підрахувати за формулою:
A = F ∙ s, (32.1)
Де А – робота, а F – сила, яка напрямлена по лінії дії вектора переміщення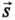 
(мал. 32.1). Формула дає вірний результат лише за умови, що сила залишається постійною впродовж усього переміщення.
Отже, робота дорівнює добутку сили на величину переміщення.
В СІ робота вимірюється в джоулях (Дж). Одиниця
Якщо на тіло діє декілька сил, то робота кожної сили обчислюється окремо (мал. 32.1). Коли сила діє в протилежному до переміщення напрямі, то її робота вважається від’ємною, такою може бути, наприклад, робота сили тертя: А mр = – Fmp ∙ s.
Якщо сила напрямлена перпендикулярно до переміщення, то її робота дорівнює нулю. Ми, наприклад, не вказали на мал. 32.1 сили
Мал. 32.1. Робота дорівнює добутку сили на переміщення
Приклад 32.1
Тіло перемістили на відстань s = 2 м, рухаючи його рівномірно в горизонтальному напрямі під дією сили F = 3 Н. Обчисліть роботу сили F і сили тертя Fтр.
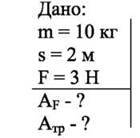
Розв’язання. Роботу сили F обчислимо за формулою: AF = F ∙ s – 3Н ∙ 2м = 6 Дж.
Оскільки тіло рухається рівномірно, то сила F компенсує дію сили Fтp, тобто дорівнює їй за величиною (і протилежна за напрямом): Fтр, = F = З Н. Робота сили тертя дорівнює:
Amp = – Fmp ∙ S = -3H ∙ 2M = – 6ДЖ.
Відповідь: робота сили F дорівнює 6 Дж, робота сили тертя дорівнює -6 Дж.
Робота в полі тяжіння
Якщо тіло рівномірно піднімають угору, долаючи силу тяжіння “mg”, чи опускають вниз під дією сили тяжіння (мал. 32.2), то робота обчислюється за тією ж формулою (32.1), але переміщення позначають літерою “h”:
А = mg ∙ h. (32.1а)
При підйомі робота сили тяжіння від’ємна, а робота підіймаючої сили – додатна.
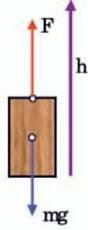
Мал. 32.2.
Приклад 32.2
Яка робота була виконана краном, що підняв бетонну плиту масою 400 кг на висоту 5 м? g = 10Н / кг.
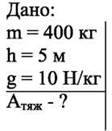
Розв’язання. Очевидно, що кран повинен діяти на плиту вгору з силою F, не меншою за mg.
Роботу сили F, яку розвиває кран, обчислимо за формулою: АF = F ∙ h = mg ∙ h = 20 000 Дж.
Відповідь. Кран виконав роботу 20 000 Дж, або 20 кДж.
Графік сили
Накреслимо графік залежності величини сили “F” від переміщення “s” для випадку, коли величина сили не змінюється, а напрям сили збігається з напрямом переміщення (мал. 32.3). Легко помітити, що добуток F ∙ S співпадає за числовим значенням з площею прямокутника abcd, тобто робота може бути обчислена як площа під графіком сили.
Цей новий спосіб обчислення роботи стає в нагоді, коли сила змінюється в процесі переміщення. Якщо ми розтягуємо пружину з деякою силою F, то величина цієї сили збільшується по мірі збільшення видовження пружини згідно закону Гука. Отже обчислювати роботу за формулою (32.1) вже не можна.
Накреслимо графік сили для випадку видовження пружини (мал. 32.4). Робота чисельно дорівнює площі трикутника abc, де ab = х – видовження, а відрізок bc = F – максимальна сила, яка утримує пружину у видовженому стані.
Таким чином, робота по видовженню пружини дорівнює:
A = 
∙ F ∙ x. (32.2)
Враховуючи, що F = k ∙ х, формулу (32.2) можна записати і так:
А = ∙ к ∙ х2 (32.3)
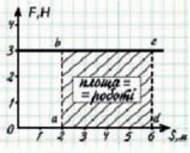
Мал. 32.3. Площа під графіком сили чисельно дорівнює роботі
Потужність
Швидкість виконання роботи називають потужністю і позначають літерою Р. Потужність дорівнює відношенню роботи до часу, впродовж якого ця робота була виконана:
Р = 
; (32.4)
Де А – робота виконана за час t.
В СІ потужність вимірюється у ватах (Вт) на честь англійського вченого та інженера Джеймса Ватта, який побудував першу парову машину. Згідно (32.4) Вт = Дж/с: при потужності один ват за одну секунду виконується робота один джоуль.
На практиці часто використовуються більші одиниці потужності – кіловат (кВт) і мегават (МВт): 1кВт = 1 000 Вт, 1 МВт = 1 000 000 Вт.
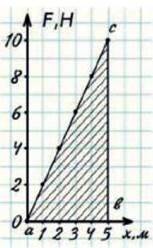
Мал. 32.4. Робота по видовженню пружини чисельно дорівнює площі трикутника аbc
Якщо у формулі (32.4) “А” замінити на F ∙ S і врахувати, що v = s/t, то отримаємо нову корисну формулу, яка дозволяє знайти потужність, знаючи силу й швидкість:
P = F ∙ v. (32.5)
За формулою (32.5) можна підрахувати потужність машини в даний момент часу. Більш потужні машини виконують роботу швидше. Наприклад, потужний двигун дозволяє автомобілю рухатися з більшим прискоренням, що покращує можливості маневрування.
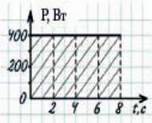
Мал. 32.5. Площа під графіком P(t) чисельно дорівнює роботі
З формули (32.4) можна отримати новий вираз для обчислення роботи:
A = P ∙ t, (32.6)
Який справедливий, коли потужність машини постійна впродовж часу t.
Якщо побудувати графік залежності потужності від часу (при постійній потужності), то стає очевидним, що площа під графіком дорівнює роботі (мал. 32.5).
Приклад 32.3
Електролічильник (мал. 32.6) визначає споживану енергію в кВт-год. Що це за фізична величина?
Розв’язання: Згідно формули (32.6) – це робота. Виразимо кВт-год. в Дж:
1 кВт – год. = 1000 Вт ∙ 3600 с = 3 600 000 Дж.
Відповідь: 1 кВт-год. дорівнює роботі 3 600 000 Дж, або 3,6 МДж.
Мал. 32.5. Електролічильник.
Підведемо підсумки
– Механічна робота дорівнює добутку сили на величину переміщення: А = F ∙ s.
– Коли сила діє в протилежному до переміщення напрямі, то її робота вважається від’ємною.
– Якщо сила напрямлена перпендикулярно до переміщення, то її робота дорівнює нулю.
– Потужність дорівнює відношенню роботи до часу, впродовж якого
Ця робота була виконана: р = .
– Робота змінної сили може бути обчислена за площею під графіком F(t).
Вправа 32
1. За якої умови формула роботи дає вірний результат?
2. Який фізичний зміст одиниці роботи Дж?
3. У яких випадках сила не виконує роботу?
4. У яких випадках сила виконує від’ємну роботу?
5. Робота якої сили від’ємна?
6. За якою формулою обчислюють роботу сили тяжіння?
7. Як можна обчислити роботу сили, яка змінюється за величиною?
8. Як називають фізичну величину, що характеризує швидкість виконання механічної роботи?
9. Як можна обчислити роботу, знаючи потужність і час роботи?
10. Як можна обчислити роботу, знаючи силу тяги машини ті її швидкість?
11. Перелічіть три різних способи розрахунку роботи.
12. У чому полягає вигода від використання потужних машин?
13. Чи виконує роботу людина, яка тримає в руці важку валізу?
14. Яку роботу виконує сила 10 Н, яка переміщує тіло на віддаль 5 м?
15. Яку роботу треба виконати, щоб ящик масою 40 кг рівномірно перемістити на 2 м по горизонтальній підлозі? Сила прикладається в напрямі переміщення. Коефіцієнт тертя ящика об підлогу становить 0,6. g = 10 Н/кг
16. М’яч масою 100 г підкинули на висоту 5 м. Знайдіть роботу сили тяжіння при русі м’яча: а) вгору; б) вниз.
17. Яку роботу треба виконати, щоб підняти з канави глибиною 5 м на поверхню бетонну брилу об’ємом 0,6 м3? Густина бетону 2600 кг/м3.
18. Знайдіть роботу, яку треба виконати, щоб видовжити пружину жорсткістю 400 Н/м на 0,02 м.
19. Як змінюється потужність двигуна автомобіля при натисканні на педаль газу?
20. Поясніть за допомогою формули (24.8), чому на крутому підйомі необхідно переключитися на понижену передачу?
21. Яка потужність двигуна, що виконує роботу 3 600 Дж за 1 хвилину?
22. Підйомний кран підняв вантаж 5 т на висоту 16 м за 1 хвилину. Яка потужність двигуна крана?
23. Обчисліть роботу двигуна за графіком потужності, наведеним на мал. 32.5: а) за 4 с; б) 8 с.
24. Бетонний блок об’ємом 2 м3 підняли під водою на висоту 1 м. Обчисліть виконану роботу. Густина бетону 2600 кг/м3.
(1 votes, average: 5.00 out of 5)
Loading...