МНОГОКУТНИК ТА ЙОГО ПЕРИМЕТР. РІВНІ ФІГУРИ
РОЗДІЛ 2 ДІЇ ПЕРШОГО СТУПЕНЯ З НАТУРАЛЬНИМИ ЧИСЛАМИ
§ 9. МНОГОКУТНИК ТА ЙОГО ПЕРИМЕТР. РІВНІ ФІГУРИ
Подивіться на малюнок 98. Ви бачите, як від точки А послідовно відкладали відрізки АВ, ВС, CD і DE, а точки А і Е сполучили відрізком АЕ. Будь-які два із цих відрізків не перетинаються і не є частинами однієї прямої. А будь-яка пряма, частиною якої є один із цих відрізків, не перетинає інші відрізки (мал. 99). Дістали нову геометричну фігуру – многокутник ABCDE (мал. 100). Точки А, В, С, D і Е – це вершини даного многокутника, а відрізки АВ, ВС, CD, DE i АЕ –
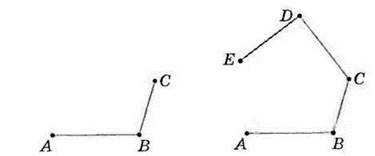
Мал. 98
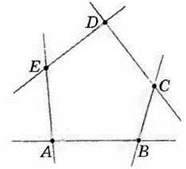
Мал. 99
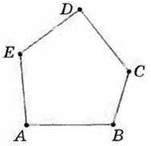
Мал. 100
Даючи назву многокутнику, треба його вершини називати послідовно, обходячи їх за стрілкою годинника або проти неї.
? Чи можна многокутнику на малюнку 100 дати назву BACDE? Ні.
Дві сторони многокутника, які мають спільну вершину, називають суміжними сторонами. Наприклад, у многокутника
ABCDEF (мал. 101) сторони АВ і ВС є суміжними, а сторони АВ і DE не є суміжними. Дві суміжні сторони утворюють кут многокутника. На малюнку 101 – це кут ABC. Його можна позначити лише однією буквою –
У будь-якого многокутника сторін рівно стільки, скільки вершин, і кутів рівно стільки, скільки вершин. Наприклад, на малюнку 101 многокутник має 6 вершин, 6 сторін і б кутів. Тому його називають шестикутником.
Позначивши кількість вершин многокутника буквою її, можемо дати йому іншу назву – n – кутник. При n = 3 отримаємо трикутник, при n = 12 – дванадцятикутник.
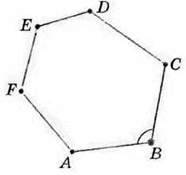
Мал. 101
Сума довжин усіх сторін многокутника називається периметром многокутника.
Периметр многокутника позначають буквою Р.
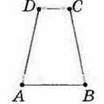
Мал. 102
Задача 1. Знайдіть периметр чотирикутника ABCD (мал. 102), якщо АВ = 4 см, ВС = AD = 5 см, CD = 2 см.
Розв’язання.
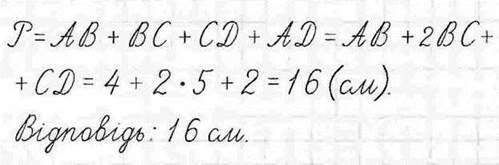
Якщо кожна сторона n – кутника дорівнює а, то його периметр можна обчислити за формулою:
Р = nа.
Серед чотирикутників особливим є прямокутник (мал. 103). У нього 4 вершини, 4 сторони і 4 кути. Усі кути прямокутника – прямі, протилежні сторони – попарно рівні, але суміжні сторони мають різні довжини. У початковій школі ви називали їх довжиною і шириною прямокутника.
Позначимо довжини суміжних сторін прямокутника буквами а і Ь. Тоді формула периметра прямокутника матиме такий вигляд:
Р = 2а + 2b.
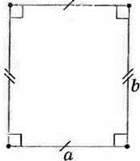
Мал. 103
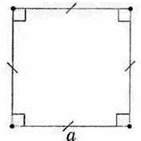
Мал. 104
Із початкової школи ви знаєте ще один особливий чотирикутник – квадрат (мал. 104). У нього всі кути – прямі (отже, він є прямокутником), а всі сторони дорівнюють одна одній. Формула периметра квадрата зі стороною а має вигляд:
Р = 4а.
? Чи кожен прямокутник є квадратом? Ні, оскільки існують прямокутники, в яких суміжні сторони не дорівнюють одна одній. Наприклад, прямокутник на малюнку 103.
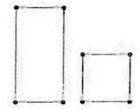
Задача. Сторони прямокутника (мал, 105) дорівнюють а см і b см (а < b), а квадрата – а см. На скільки периметр прямокутника більший за периметр квадрата?
Розв’язання. Позначимо периметр прямокутника Р1, а периметр квадрата – Р2. Тоді Р1 = 2а + 2b (см), а Р2= 4а (см). Знайдемо різницю Р1 і Р2:
Р1 – Р2 = 2а + 2b – 4а = 2а + 2b – 2а – 2а = 2b – 2а (см).
Отже, периметр прямокутника зі сторонами а см і b см (а < b) більший за периметр квадрата зі стороною а см на 2b – 2а (см).
Мал. 105

Мал. 106
Мал. 107
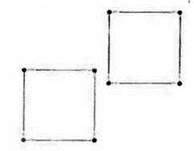
Подивіться на малюнок 106. Ви бачите, що два прямокутники мають відповідно рівні сторони і їх можна сумістити, накладаючи один на одного. У двох квадратів на малюнку 107 довжина сторін та сама і їх теж можна сумістити накладанням. Якою б не була фігура, завжди можна знайти таку фігуру, яка з нею суміститься накладанням.
Дві фігури називаються рівними, якщо вони суміщаються накладанням.
Отже, на малюнку 106 зображено рівні прямокутники, а на малюнку 107 – рівні квадрати. Зрозуміло, що рівні фігури мають рівні периметри. Пізніше ви дізнаєтесь про інші властивості рівних фігур.
Дізнайтеся більше
1. У метричній системі, якою ми користуємось, основною одиницею вимірювання довжини є метр. Метр (від грец. metron – міра, розмір) дорівнює довжині шляху, який проходить у вакуумі світло за 1 /299 792 458 частину секунди.
2. В астрономії користуються власними одиницями вимірювання відстаней. Наприклад, світловий рік (скорочено “св. р.”). 1 св. р. дорівнює відстані, яку світло проходить за один рік. Оскільки швидкість світла у вакуумі дорівнює 299 792 458 м/с, то світловий рік становить 9 460 730 472 581 км.
РОЗВ’ЯЖІТЬ ЗАДАЧІ
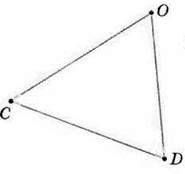
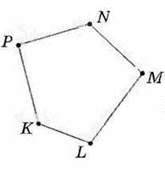
304. Назвіть многокутники, які зображено на малюнках 108 – 110. Назвіть сторони, пари суміжних сторін, кути даних многокутників.
Мал. 108
Мал. 109
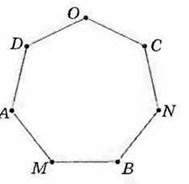
Мал. 110
305. Скільки вершин, сторін, кутів має n-кутник, якщо:
1) n = 7; 2) n = 12; 3)n=105?
Як називається такий многокутник?
306. Накресліть:
1) чотирикутник;
2) п’ятикутник;
3) шестикутник.
307. Назвіть пари рівних сторін прямокутника:
1 ) ABCD (мал. 111);
2) MNPK (мал. 112).

Мал. 111
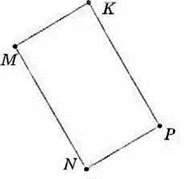
Мал. 112
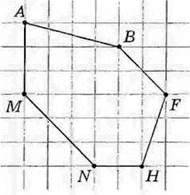
Мал. 113
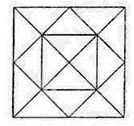
Мал. 114
308. Чи правильно записано формулу периметра прямокутника ABCD:
1 )Р=АВ + ВС;
2) Р = 2АВ+2ВС;
3) P = 2AB + 2CD?
309. Обчисліть периметр п’ятикутника, сторони якого дорівнюють:
1) 3 см, 6 см, 7 см, 2 см, 5 см;
2) 65 см, 26 см, 34 см, 19 см, 11 см.
310. Кожна сторона n-кутника дорівнює с. Запишіть формулу для знаходження його периметра, якщо:1)n = 5; 2)n=10; 3)n = 78.
311. Обчисліть периметр n-кутника, кожна сторона якого дорівнює 5 см, якщо:
1) n= 10; 2)n = 200; 3) n= 1000.
312. Побудуйте чотирикутник. Проведіть необхідні вимірювання та знайдіть його периметр.
313. Побудуйте многокутник, рівний многокутнику, зображеному на малюнку 113.
314 Які многокутники зображено на малюнку 114? Скільки зображено чотирикутників? Шестикутників?
315. Чи є чотирикутник ABCD прямокутником, якщо:
1) ∠А = 90°, ∠B = 80°, ∠С = 90°, ∠D=100°;
2) ∠А = 90°, ∠B = 90°, ∠С = 90°, ∠D = 90°;
3) АВ = 4 см, ВС = 8 см, CD = 8 см, DA = 4 см;
4) АВ = 4 см, ВС = 4 см, CD = 4 см, DA = 8 см?
Мал. 115
Мал. 116
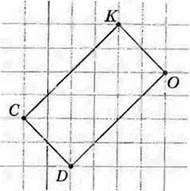
316. Побудуйте прямокутник, рівний прямокутнику, зображеному на малюнку 115.
317. Побудуйте прямокутник, сторони якого вдвічі більші за сторони прямокутника на малюнку 115.
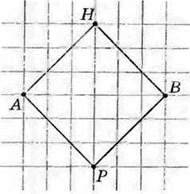
318. Побудуйте квадрат, рівний квадрату, зображеному на малюнку 116.
319. Побудуйте квадрат, сторона якого втричі менша від сторони квадрата на малюнку 116.
320. Дано квадрат. Знайдіть невідомі величини за таблицею 9.
Таблиця 9
Сторона Квадрата | 4 см 40 мм | 12 дм | ||
Периметр Квадрата | 20 см | 64 м | 400 мм | 24 км |
321. Дано прямокутник. Знайдіть невідомі величини за таблицею 10.
Таблиця 10
Довжина | 20 см | 8 см | 56 дм | 120 мм | ||
Ширина | 15 см | 23 см | 10 см | 32 cм | 24 см | 45 см |
Периметр | 60 см | 124 см |
322. Одна сторона прямокутника дорівнює 246 см, а друга – на 98 см менша. Знайдіть периметр прямокутника.
323. Одна сторона прямокутника дорівнює 56 м, а друга – на 23 м більша. Знайдіть периметр прямокутника.
324. Периметр прямокутника дорівнює 64 см. Знайдіть довжину прямокутника, якщо його ширина дорівнює 6 см.
325.Периметр прямокутника дорівнює 48 дм. Знайдіть ширину прямокутника, якщо його довжина дорівнює 8 дм.
326. Знайдіть сторону квадрата, якщо його периметр дорівнює 16 т.
327. Як зміниться периметр n-кутника, якщо кожну його сторону збільшити на 7 см?
328. Сторона ВС чотирикутника ABCD дорівнює 28 см, що вдвічі більше за AD. Сторона АВ на 9 см менша від ВС і на 3 см більша за CD. Знайдіть периметр чотирикутника.
329. Сторона АВ чотирикутника ABCD дорівнює 150 см. Сторона AD втричі більша за АВ, сторона ВС – на 34 см менша від АВ. Знайдіть CD, якщо периметр чотирикутника дорівнює 916 см.
330. Найменша сторона десятикутника дорівнює 4 см. Кожна його наступна сторона більша за попередню на 2 см. Знайдіть периметр десятикутника.
331. Найбільша сторона дев’ятикутника дорівнює 45 см. Кожна його наступна сторона менша від попередньої на 3 см. Знайдіть периметр дев’ятикутника.
332 Периметр прямокутника дорівнює 20 см. Знайдіть довжину прямокутника, якщо вона на 2 см більша за його ширину.
333. Прямокутник має сторони 2 см і 8 см. Знайдіть сторону квадрата, периметр якого дорівнює периметру даного прямокутника.
334. Одна сторона прямокутника дорівнює m, а друга – на n більша. Знайдіть периметр прямокутника, якщо:
1) m = 6 см, n = 20 мм; 2) m = 8 дм, n = 4 см.
335. Одна сторона прямокутника дорівнює 17 м, а друга – на 65 см менша. Знайдіть периметр прямокутника.
336. Периметр прямокутника дорівнює 34 дм. Знайдіть довжину прямокутника, якщо його ширина дорівнює 500 мм.
337. Футбольне поле має форму прямокутника, розміри якого 100 м і 75 м. Знайдіть розміри баскетбольного майданчика прямокутної форми, якщо його ширина у 5 разів менша від ширини футбольного поля, а довжина – на 72 м менша від довжини футбольного поля.
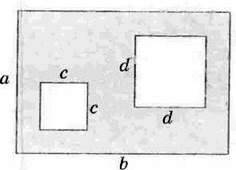
Мал. 118
338. Знайдіть сторону квадрата, периметр якого дорівнює 7 м.
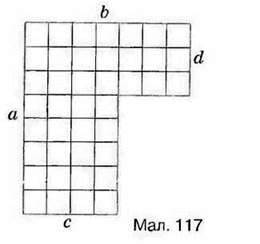
339. Запишіть вирази для знаходження периметра фігур, зображених на малюнках 117, 118.
340. Найменша сторона семикутника дорівнює а. Кожна його наступна сторона більша за попередню на с. Знайдіть периметр семикутника.
341. Сторона АВ прямокутника ABCD утричі більша за сторону ВС. Знайдіть сторони прямокутника, якщо його периметр дорівнює 72 см.
342. Папір має форму прямокутника, одна сторона якого дорівнює 4 см, а друга – 9 см. Розріжте цей прямокутник на дві рівні частини так, щоб можна було, склавши їх, отримати квадрат. Знайдіть його периметр.
ЗАСТОСУЙТЕ НА ПРАКТИЦІ
343. Кімната у формі прямокутника має розміри 3 х 4 м. Скільки метрів плінтуса потрібно купити для цієї кімнати?
344. Садок має форму прямокутника зі сторонами 6 м і 10 м. Чи вистачить 30 м паркану для того, щоб обгородити сад?
345. Маємо набір паличок: 4 палички завдовжки 1 см, 4 палички завдовжки 2 см, 7 паличок завдовжки 3 см і 5 паличок завдовжки 4 см. Чи можна з усіх паличок цього набору скласти прямокутник?
346. Ширина лінолеуму 2 м. Скільки метрів лінолеуму буде потрібно, щоб покрити підлогу, розміром 5 х4м?
347. Обчисліть:
1) 25 кг 900 г + 24 кг 650 г; 2) 34 кг 25 г – 15 кг 70 г,
348. З одного пункту в протилежних напрямках вирушили два катери зі швидкостями 25 км/год і 30 км/год. На якій відстані один від одного будуть катери через 1 год?