Множення. Переставна властивість множення
Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ
§ 3. МНОЖЕННЯ І ДІЛЕННЯ НАТУРАЛЬНИХ ЧИСЕЛ
Вивчивши матеріал цього параграфа, ви розширите і поглибите свої знання про дії множення і ділення натуральних чисел. Ви ознайомитеся з новою арифметичною дією – піднесенням до степеня, продовжите знайомство з геометричними фігурами – прямокутним паралелепіпедом і пірамідою. Ви дізнаєтеся, що називають діленням з остачею; що таке квадрат і куб числа; які властивості мають такі величини, як площа та об’єм. Навчитеся знаходити площу прямокутника та
16. Множення. Переставна властивість множення
Накреслимо на аркуші в клітинку прямокутник із сторонами 5 см і 3 см. Розіб’ємо його на квадрати із стороною 1 см (рис. 139). Як підрахувати кількість цих квадратів?

Рис. 139
Можна, наприклад, міркувати так. Прямокутник розділено на три ряди, у кожному з яких є п’ять квадратів. Тому шукане число дорівнює 5 + 5 + 5=15. У лівій частині записаної рівності знаходиться сума рівних доданків. Як ви знаєте, таку суму записують коротше: 5 ∙ 3. Отже, 5 ∙ 3 = 15.
У рівності а ∙ b = с числа а і b називають множниками,
Можна записати. що 5-3 = 5 + 5 + 5.
Аналогічно:
3 ∙ 5 = 3 + 3 + 3 + 3 + 3;
7 ∙ 4 = 7 + 7 + 7 + 7;
1 ∙ 6 = 1 + 1 + 1 + 1 + 1 +1;
0 ∙ 5 = 0 + 0 + 0 + 0 + 0.
У буквеному вигляді записують так:
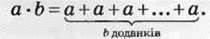
Добутком числа а на натуральне число Ь, яке не дорівнює 1, називають суму, що складається з Ь доданків, кожний з яких дорівнює а.
А якщо b = 1? Тоді доведеться розглядати суму, яка складається з одного доданка, що в математиці не прийнято. Тому домовились, що
А ∙ 1 = а
Якщо b = 0, то домовилися вважати, що
А ∙ 0 = 0
Зокрема,
0 ∙ 0 = 0
Розглянемо добутки 1-а і 0 ∙ а, де а – натуральне число, відмінне від 1.
Маємо:
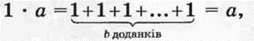
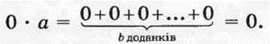
Тепер можна зробити такі висновки.
Якщо один із двох множників дорівнює 1, то добуток дорівнює іншому множнику:
А ∙ 1 = 1 ∙ а = а
Якщо один із множників дорівнює нулю, то добуток дорівнює нулю:
А ∙ 0 = 0 ∙ а = 0
Добуток двох чисел, відмінних від нуля, нулем бути не може.
Якщо добуток дорівнює нулю, то хоча б один із множників дорівнює нулю.
Кількість квадратів на рисунку 139 ми підрахували так:
5 + 5 + 5 = 5 ∙ 3 = 15.
Проте цей підрахунок можна було зробити й іншим способом. Прямокутник поділено на п’ять стовпчиків, у кожному з яких є три квадрати. Тому шукане число квадратів дорівнює
3 + 3 + 3 + 3 + 3 = 3 ∙ 5 = 15.
Підрахунок квадратів на рисунку 139 двома способами ілюструє переставну властивість множення: від перестановки множників добуток не змінюється.
Цю властивість у буквеному вигляді записують так:
Ab = bа
Ви вмієте множити письмово (у стовпчик) багатоцифрове число на двоцифрове. Аналогічно виконують множення будь-яких двох багатоцифрових чисел.
Наприклад:
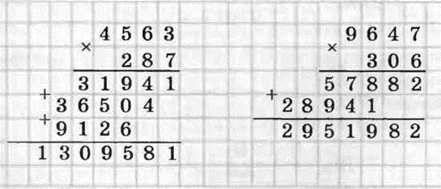
Цей спосіб зручний тим, що множити усно доводиться тільки одноцифрові числа.
Розглянемо задачі, у розв’язуванні яких використовують дію множення.
ПРИКЛАД 1 У саду ростуть вишні, яблуні та груші. Вишень є 24 дерева, що в 6 разів менше, ніж яблунь, і на 18 дерев менше, ніж груш. Скільки всього дерев росте в саду?
Розв’язання. 1) 24 ∙ 6 = 144 (дерева) – становлять яблуні.
2) 24 + 18 = 42 (дерева) – становлять груші.
3) 24 + 144 + 42 = 210 (дерев) – росте в саду.
Відповідь: 210 дерев.
ПРИКЛАД2 3 одного міста одночасно в одному напрямі виїхали вантажівка зі швидкістю 48 км/год і легковий автомобіль зі швидкістю 64 км/год. Якою буде відстань між ними через 3 год після початку руху?
Розв’язання. 1) 64 – 48 = 16 (км) – на стільки збільшується відстань між автомобілями щогодини.
2) 16 ∙ 3 = 48 (км) – відстань між автомобілями через 3 год.
Відповідь: 48 км.
ПРИКЛАД3 3 одного села в протилежних напрямах вирушили одночасно вершник зі швидкістю 14 км/год і пішохід зі швидкістю 4 км/год. Якою буде відстань між ними через 4 год після початку руху?
Розв’язання. 1) 14 + 4 = 18 (км) – на стільки збільшується відстань між вершником і пішоходом щогодини.
2) 18 ∙ 4 = 72 (км) – відстань між вершником і пішоходом через 4 год.
Відповідь: 72 км.
ПРИКЛАД4 Від двох пристаней одночасно назустріч один одному відійшли два катери, які зустрілися через 5 год після початку руху. Один із катерів рухався зі швидкістю 28 км/год, а другий – зі швидкістю 36 км/год. Знайдіть відстань між пристанями.
Розв’язання. 1) 28 + 36 = 64 (км) – на стільки зближувались катери щогодини.
2) 64 ∙ 5 = 320 (км) – відстань між пристанями.
Відповідь: 320 км.
Розв’язуємо усно
1. Чому дорівнює сума:
1) 20 + 20 + 20; 3) 7 + 7 + 7 + 7 + 7?
2) 12 + 12 + 12 + 12;
2. Обчисліть:
1) 6 + 4 ∙ 3 – 2; 3) 6 + 4 ∙ (3 – 2);
2) (6 + 4) ∙ 3 – 2; 4) (6 + 4) ∙ (3 – 2).
3. Знайдіть добуток чисел 14 і 6.
4. Збільште число 18 у 3 рази.
5. Знайдіть бічну сторону рівнобедреного трикутника, якщо його периметр на 12 см більший за основу.
6. Визначте вид трикутника, дві сторони якого дорівнюють 8 см і 12 см, а периметр – 28 см.
7. Знайдіть периметр квадрата, якщо він більший за його сторону на 18 см.
Вправи
389. Запишіть суму у вигляді добутку:
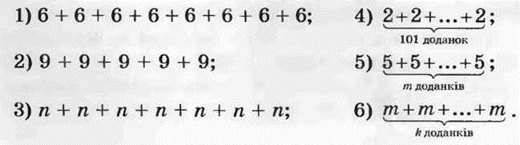
390.° Виконайте множення:
1) 516 ∙ 32; 4) 314 ∙ 258; 7) 626 ∙ 480;
2) 418 ∙ 46; 5) 133 ∙ 908; 8) 1234 ∙ 567;
3) 4519 ∙ 52; 6) 215 ∙ 204; 9) 2984 ∙ 4006.
391.° Виконайте множення:
1) 706 ∙ 53; 4) 591 ∙ 289; 7) 934 ∙ 260;
2) 304 ∙ 29; 5) 465 ∙ 506; 8) 2468 ∙ 359;
3) 5245 ∙ 67; 6) 328 ∙ 406; 9) 1234 ∙ 2007.
392.° Обчисліть:
1) 704 ∙ 69 + 1424; 5) (294 + 16) ∙ (348 – 279);
2) 412 ∙ 42 -7304; 6) 294 + 16 ∙ 348 – 279;
3) (938 – 543) ∙ 34; 7) (294 + 16) ∙ 348 – 279;
4) 85 ∙ (870 – 567); 8) 294 + 16 ∙ (348 – 279).
393. Обчисліть:
1) 603 ∙ 84 + 2536; 3) 64 ∙ 96 – 77;
2) 318 ∙ 56 -5967; 4) 64 ∙ (96 – 77).
394.° Обчисліть значення виразу:
1) 17x + 432, якщо х = 58;
2) (739 – х) ∙ у, якщо х = 554, у = 1900.
395.° Обчисліть значення виразу:
1) 976 – 24х, якщо х = 36;
2) х ∙ 63 – у, якщо х = 367, у = 19742.
396.° Виконайте множення:
1) 693 ∙ 100; 3) 540 ∙ 20; 5) 760∙350;
2) 974 ∙ 1000; 4) 120 ∙ 400; 6) 460∙1800.
397.° Виконайте множення:
1) 214 ∙ 10; 3) 10 000 ∙ 546; 5) 580 ∙240;
2) 100 ∙ 328; 4) 140 ∙ 80; 6) 270 ∙ 3000.
398.° Готуючись до школи, Буратіно купив 34 зошити по 12 сольдо і 18 зошитів по 16 сольдо. Скільки сольдо заплатив Буратіно за всі зошити?
399.° Кіт Матроскін продав 42 л молока по 96 к. за літр і 16 кг сиру по 2 грн за кілограм. Скільки грошей отримав Матроскін за свій товар?
400.° Вирушивши в похід, Барвінок 14 год плив річкою на човні зі швидкістю 8 км/год і йшов пішки 23 год зі швидкістю 4 км/год. Який шлях, річкою чи суходолом, він подолав більший і на скільки кілометрів?
401.° Івасик-Телесик плив на моторному човні 5 год річкою зі швидкістю 27 км/год і 7 год озером зі швидкістю 21 км/год. Який шлях, річкою чи озером, був довшим і на скільки кілометрів?
402.° До школи завезли апельсини, мандарини та лимони. Апельсинів було 94 кг, що в 7 разів менше, ніж мандаринів, і на 16 кг більше, ніж лимонів. Скільки всього кілограмів фруктів було завезено до школи?
403.° Школі виділили 8000 грн на покупку телевізора, фотоапарата і DVD-програвача. Фотоапарат коштує 984 грн, що в 4 рази менше, ніж коштує телевізор, і на 1488 грн менше, ніж DVD-програвач. Чи вистачить виділених грошей на покупку?
404.° Знайдіть значення виразу:
1) (318 ∙ 207 – 64 934) ∙ 276 + 604 ∙ 88;
2) 869 ∙ (61 124 – 488 ∙ 125) – 509 ∙ 74.
405.° Знайдіть значення виразу:
1) (214 ∙ 104 + 7544) ∙ 35 – 508 ∙ 722;
2) 647 ∙ (36 900 – 255 ∙ 144) – 318 ∙ 92.
406.° З одного порту в інший одночасно відійшли теплохід і катер. Швидкість теплохода дорівнює 28 км/год, а швидкість катера – 36 км/год. Якою буде відстань між ними через 5 год після початку руху?
407.° З одного села в одному напрямі вирушили одночасно два велосипедисти. Один із них їхав зі швидкістю
12 км/год, а другий – зі швидкістю 9 км/год. Якою буде відстань між ними через 6 год після початку руху?
408.° З однієї станції в протилежних напрямах одночасно відійшли два поїзди. Один із них рухався зі швидкістю 64 км/год, а другий – зі швидкістю 57 км/год. Якою буде відстань між ними через 9 год після початку руху?
409.° З одного міста в протилежних напрямах виїхали одночасно два автомобілі. Швидкість одного з них дорівнювала 74 км/год, що на 8 км/год більше, ніж швидкість другого. Якою буде відстань між ними через 7 год після початку руху?
410.° Із міст Конотоп і Сміла одночасно назустріч один одному виїхали велосипедист і легковий автомобіль. Велосипедист їхав зі швидкістю 11 км/год, а автомобіль – у 7 разів швидше. Знайдіть відстань між цими містами, якщо велосипедист і автомобіль зустрілися через 4 год після початку руху.
411.°Із двох селищ одночасно назустріч один одному вирушили велосипедист і пішохід. Пішохід рухався зі швидкістю 3 км/год, що в 4 рази менше від швидкості велосипедиста. Знайдіть відстань між селищами, якщо велосипедист і пішохід зустрілися через 3 год після початку руху.
412.° Чи завжди добуток двох натуральних чисел більший за їх суму?
413.° Як зміниться добуток двох натуральних чисел, якщо:
1) один із множників збільшити у 8 разів;
2) один із множників зменшити в 5 разів;
3) кожний із множників збільшити в 6 разів;
4) один множник збільшити в 13 разів, а другий – у 40 разів;
5) один множник збільшити у 12 разів, а другий зменшити в 3 рази?
414.°° Із двох хуторів, відстань між якими дорівнює 3 км, вийшли одночасно назустріч один одному два пішоходи. Один із них рухався зі швидкістю 5 км/год, а другий – зі швидкістю 4 км/год. Якою буде відстань між пішоходами через 2 год після початку руху?
415.°°Замість зірочок поставте такі цифри, щоб множення було виконано правильно:
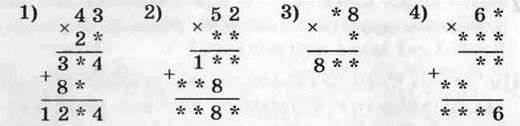
416.°° Замість зірочок поставте такі цифри, щоб множення було виконано правильно:

417.°°При яких значеннях а є правильною рівність:
1) а ∙ 5 = 5; 4) а ∙ 1 = 1; 7) 0 ∙ а = а;
2) а ∙ 5 = 0; 5) а ∙ 1 = а; 8) 0 ∙ а = 0;
3) а ∙ 5 = а; 6) а ∙ а = а; 9) а ∙ 1 = 0?
418.°°Сума і добуток чотирьох натуральних чисел дорівнюють 8. Що це за числа?
419.* У записі 1*2*3*4*5 замініть зірочки на знак “+” або знак “∙” та поставте дужки так, щоб значення отриманого виразу дорівнювало 100.
Вправидля повторення
420. Знайдіть величину кута АВМ (рис. 140), якщо ∠MBK – прямий і ∠ABM = ∠CBK.
421. Кут ABC дорівнює 72°, промінь BD – бісектриса кута ABC, промінь BE – бісектриса кута ABD. Обчисліть величину кута СВЕ.
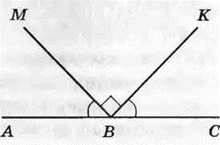
Рис. 140
422. За формулою а = b : 4 – 6 знайдіть значення а, якщо: 1) b – 600; 2) b = 64; 3) b = 24.
423. Сума довжин першої і другої сторін трикутника дорівнює 33 см, першої і третьої – 39 см, другої і третьої – 42 см. Знайдіть периметр трикутника.
Задачавід Мудрої Сови
424. 1) Складіть із 10 сірників три квадрати.
2) Складіть із 19 сірників шість квадратів.
3) Які чотири сірники треба забрати (рис. 141), щоб залишилося п’ять квадратів?
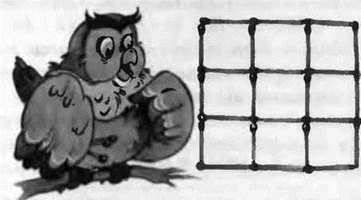
Рис. 141