Найбільший спільний дільник
Розділ 1 Подільність натуральних чисел
§6. Найбільший спільний дільник
Розглянемо задачу.
Задача. Яку найбільшу кількість однакових подарунків можна скласти, маючи 32 цукерки “Білочка” і 24 цукерки “Чебурашка”, якщо треба використати всі цукерки і у кожному подарунку мають бути цукерки двох видів?
Розв’язання. Кожне із чисел 32 і 24 має ділитися на кількість подарунків. Тому спочатку випишемо всі дільники числа 32:
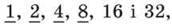а потім – усі дільники числа 24: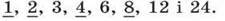 
Спільними
Отже, можна скласти 8 подарунків, у кожному з яких буде 4 цукерки “Білочка” (32 : 8 = 4) і 3 цукерки “Чебурашка” (24 : 8 = 3).
– Найбільшим спільним дільником кількох натуральних чисел називають найбільше натуральне число, на яке ділиться кожне з даних чисел.
Найбільший спільний дільник чисел а і b позначають так: НСД (a; b). Для попередньої задачі можна записати НСД (32; 24) = 8.
У розглянутій задачі знайшли найбільший спільний дільник невеликих чисел 32 і 24, записавши всі дільники
– найбільший спільний дільник кількох чисел дорівнює добутку спільних простих множників цих чисел.
Приклад 1. Знайти НСД (630; 1470).
Розв’язання. Розкладемо числа 630 і 1470 на прості множники і підкреслимо ті з них, які є спільними в обох розкладах (а саме 2, 3, 5 і 7):
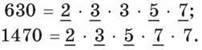
Отже, НСД (630; 1470) = 2 ∙ 3 ∙ 5 ∙ 7 = 210. Приклад 2. Знайти НСД (60; 140; 220).
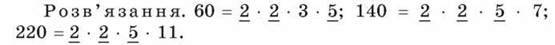
Отже,
НСД (60; 140; 220) = 2 ∙ 2 ∙ 5 = 20.
Маємо таке правило:
– щоб знайти найбільший спільний дільник кількох чисел, достатньо:
1) розкласти дані числа на прості множники;
2) виписати всі спільні прості множники в знайдених розкладах і обчислити їх добуток.
Якщо серед даних чисел є число, на яке діляться інші з даних чисел, то це число і буде найбільшим спільним дільником даних чисел.
Приклад 3. Знайти НСД (8; 64; 320).
Розв’язання. Оскільки числа 64 і 320 діляться на 8, то НСД (8; 64; 320) = 8.
Якщо розклади даних чисел на прості множники не мають спільних множників, то найбільшим спільним дільником цих чисел буде число 1.
– Два натуральних числа, найбільший спільний дільник яких дорівнює 1, називають взаємно простими числами.
Наприклад, числа 12 і 35 – взаємно прості, бо 12 = 2 ∙ 2 ∙ 3, 35 = 5 ∙ 7 і НСД (12; 35) = 1. Числа ж 15 і 18 не є взаємно простими, бо мають спільний дільник 3.
А ще раніше…
Цікавий спосіб знаходження найбільшого спільного дільника двох чисел описав у своїй книзі “Начала” давньогрецький математик Евклід (бл. 300 р. до н. е.). Для цього він ділив більше число на менше, менше – на одержану остачу, першу остачу – на другу і т. д. Остання відмінна від нуля остача й була шуканим НСД двох чисел. Цей спосіб отримав назву алгоритм Евкліда.
Знайдемо, наприклад, за цим алгоритмом НСД (407; 148):
Отже,
НСД (407; 148) = 37.
Яке число називають найбільшим спільним дільником двох чисел? Як знайти найбільший спільний дільник двох чисел? Число а є дільником числаb. Чому дорівнює НСД (а; b)? Які два числа називають взаємно простими?
96. (Усно) Чи є число 5 спільним дільником чисел:
1) 30 і 25; 2) 48 і 15?
97. (Усно) Знайди спільні дільники та найбільший спільний дільник чисел:
1) 2 і 4; 2) 6 і 15; 3) 8 і 18.
98. Знайди найбільший спільний дільник чисел а і b, якщо:
1) а = 2 ∙ 3 ∙ 5 ∙ 11 і b = 2 ∙ 3 ∙ 11 ∙ 13;
2) а = 3 ∙ 5 ∙ 5 ∙ 7 і b = 5 ∙ 5 ∙ 19.
99. Знайди найбільший спільний дільник чисел с і d, якщо:
1) с = 3 ∙ 3 ∙ 5 ∙ 11 і d = 3 ∙ 5 ∙ 11 ∙ 13;
2) с = 2 ∙ 3 ∙ 5 ∙ 5 і d = 3 ∙ 5 ∙ 7.
100. (Усно) Чи є взаємно простими числа:
1) 6 і 9; 2) 7 і 8; 3) 9 і 12; 4) 4 і 11?
101. (Усно) Серед чисел 2, 7, 14 і 20 знайди всі пари взаємно простих чисел.
102. Знайди найбільший спільний дільник чисел:
1) 78 і 195; 2) 35 і 18; 3) 210 і 120;
4) 735 і 70; 5) 4, 24 і 32; 6) 36, 54 і 72.
103. Знайди найбільший спільний дільник чисел:
1) 24 і 40; 2) 70 і 110; 3) 49 і 48;
4) 231 і 273; 5) 5, 25 і 45; 6) 150, 375 і 600.
104. Знайди найбільший спільний дільник чисельника і знаменника дробу:
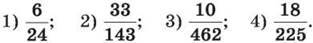
105. Доведи, що: 1) числа 35 і 72 є взаємно простими;
2) числа 209 і 171 не є взаємно простими.
106. Доведи, що: 1) числа 299 і 184 не є взаємно простими; 2) числа 26 і 45 є взаємно простими.
107. Чи є взаємно простими числа:
1) 3 і 100; 2) 35 і 133; 3) 143 і 209; 4) 2010 і 2012?
108. Чи є взаємно простими числа:
1) 7 і 48; 2) 21 і 161; 3) 66 і 455; 4) 2005 і 3005?
109. Запиши всі правильні дроби зі знаменником 18, у яких чисельник і знаменник – взаємно прості числа.
110. Запиши всі неправильні дроби із чисельником 20, у яких чисельник і знаменник – взаємно прості числа.
111. Яку найбільшу кількість однакових подарунків можна скласти, маючи 60 цукерок і 45 яблук, так, щоб використати всі цукерки і яблука та щоб кожен подарунок містив і цукерки, і яблука.
112. У яку найбільшу кількість магазинів можна порівну розподілити для продажу 108 DVD-дисків з мультфільмами і 120 дисків із фільмами про тварин? По скільки дисків кожного жанру отримає кожний магазин?
113. У шостих класах 24 хлопчики і 36 дівчаток. Учнів поділили на групи для привітання ветеранів так, щоб в усіх групах була однакова кількість дівчаток і однакова кількість хлопчиків. Скількох ветеранів привітали, якщо їх більше за 7?
114. В одному потязі 252 купейних місця, а в іншому – 396 купейних місць. По скільки купейних вагонів у кожному потязі, якщо в усіх купейних вагонах кількість місць є однаковою і їх більше за 20?
115. Із 210 білих, 150 жовтих і 90 червоних троянд необхідно скласти однакові букети так, щоб у кожному букеті були троянди всіх трьох кольорів. Яку найбільшу кількість таких букетів можна скласти? По скільки троянд кожного кольору буде в кожному букеті?
116. Шлях від А до В завдовжки 360 км автомобіль проїхав за 4 год, а повернувся назад – за 5 год. Яка середня швидкість автомобіля за весь час руху?
117. Автомобіль їхав 2 год зі швидкістю 72,4 км/год і 3 год зі швидкістю 71,6 км/год. Знайди середню швидкість автомобіля за весь час руху.
118. Вкладник поклав до банку 8000 грн під 15 % річних. Скільки грошей буде на рахунку вкладника через рік; через два роки?
119. Знайди останню цифру числа:
1) 52015; 2) 320; 3) 22000.
(2 votes, average: 5.00 out of 5)
Loading...