ПРОПОРЦІЯ ТА її ВЛАСТИВОСТІ
Розділ 3 ВІДНОШEННЯ І ПРОПОРЦІЇ
§13. ПРОПОРЦІЯ ТА її ВЛАСТИВОСТІ
Ви знаете, що два вирази, які мають рівні значення, можна прирівняти. Наприклад, можна прирівняти відношення 1,2 : 0,3 і 16 : 4, оскільки їх значення дорівнюють 4. Отже, можна записати рівність:
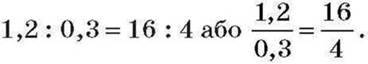
Такі рівності мають спеціальну назву – пропорція.
Пропорцією називається рівність двох відношень.
Зверніть увагу:
Пропорція стверджує, що відношення в лівій і правій її частинах мають рівні значення.
Записують:
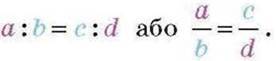
Читають:
Числа а і d називають крайніми членами пропорції у а числа b і с – середніми членами пропорції (мал. 12).
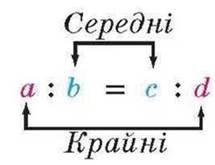
Мал. 12
Зверніть увагу:
Пропорції складають тільки для чисел, відмінних від нуля.
Обчислимо добутки крайніх і середніх членів пропорції 1,2 : 0,3 = 16 : 4. Для крайніх членів отримаємо
1,2 ∙ 4 = 4,8, а для середніх членів – 0,3 ∙ 16 = 4,8. Отже, ці добутки дорівнюють один одному: 1,2 ∙ 4 = 0,3 ∙ 16. У цьому полягає основна властивість пропорції.
Основна властивість
Добуток крайніх членів пропорції дорівнює добутку її середніх членів:
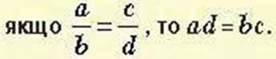
І навпаки: якщо ad = bc і числа а, b, с id не дорівнюють нулю, то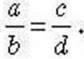 
Задача 1 . Чи є рівність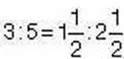 
пропорцією?
Розв’язання.
Спосіб 1. Застосуємо означення пропорції:
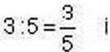
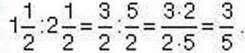
Значення відношень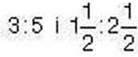 
є рівними, отже, рівність 
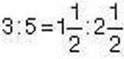– пропорція.
Спосіб 2. Перевіримо, чи виконується основна властивість пропорції: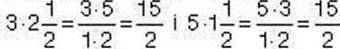 
Отримали, що добуток крайніх членів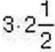 
дорівнює добутку середніх членів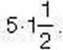 
Отже, рівність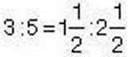 
– пропорція.
У пропорції 1,2: 0,3 =16:4 поміняємо місцями крайні члени 1,2 і 4. Дістали нову рівність 4 : 0,3 = 16 : 1,2. Ця рівність теж є пропорцією. Справді, унаслідок перестановки крайніх членів 1,2 і 4 і їх добуток і добуток середніх членів не змінився, тому нова рівність – пропорція. Так само добутки крайніх членів і середніх членів не зміняться, якщо в пропорції поміняти місцями середні члени: 1,2 : 16 = 0,3 : 4. Але отримані пропорції 1,2 : 16 = 0,3: 4 і 4 : 0,3 = 16 : 1,2 відрізняються від даної пропорції 1,2 : 0,3 = 16 : 4, оскільки мають інші значення відношень. У даній пропорції воно дорівнює 4, а в отриманих пропорціях –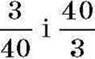 
відповідно.
Інакше кажуть: пропорційне співвідношення чисел змінилось.
У пропорціях 1,2:16 = 0,3:4 і 4 :0,3 = 16:1,2 значен ня їх відношень – це взаємно обернені числа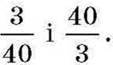 
Тому такі пропорції називають взаємно оберненими. У взаємно обернених пропорціях пропорційне співвідношення чисел є однаковим з точністю до порядку порівняння. Справді, в обох пропорціях порівнюють дві якісь величини – меншу і більшу, наприклад, товщину лінійки і товщину підручника. Але в першій пропорції зіставляють меншу величину з більшою, а в другій, навпаки, – більшу з меншою, причому ті самі величини. Можна сказати і так: друга пропорція – це перша пропорція, яку записали справа наліво. У ній одночасно поміняли місцями і середні, і крайні члени. Будемо вважати, що при переході від даної пропорції до оберненої і навпаки пропорційне співвідношення чисел не змінюється.
? Чи зміниться пропорційне співвідношення чисел, якщо її середні члени поміняти місцями з відповідними крайніми членами? Ні. Справді, якщо в кожному відношенні пропорції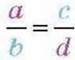 
поміняти місцями його члени – а з b і с із d, то дістанемо рівність обернених відношень: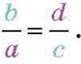 
А така рівність є пропорцією, взаємно оберненою з даною.
Спираючись на основну властивість пропорції, можна знаходити невідомий член пропорції.
Задача 2. Знайдіть невідомий член пропорції:
1) х : 28 = 3 :1 2; 2)30 :у = 5 :8.
Розв’язання. 1. Невідомим е крайній член пропорції х : 28 = 3 : 12. За основною властивістю пропорції: 12х= 28 ∙ 3.
Звідси: 
2. Невідомим е середній член пропорції 30 : у = 5 : 8. За основною властивістю пропорції: 5у = 30 ∙ 8. Звідси: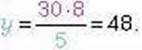 
Запам’ятайте!
Правила знаходження невідомого члена пропорції
1. Щоб знайти невідомий крайній член пропорції, треба добуток її середніх членів поділити па відомий крайній член пропорції.
2. Щоб знайти невідомий середній член пропорції, треба добуток її крайніх членів поділити на відомий середній член пропорції.
Дізнайтеся більше
1. Термін “пропорція” походить від латинського proportio – “співвідношення”.
2. Золотим перерізом називають поділ відрізка на дві нерівні частини а і b (мал. 13), за якого менша частина так відноситься до більшої частини, як більша частина відноситься до всього відрізка, тобто а : b = b : с. Значення цього відношення приблизно дорівнює 0,618.
Мал. 13
Вважають, що поняття золотого перерізу було відоме в Стародавньому Єгипті. І справді, пропорції піраміди Хеопса, храмів, барельефів, предметів побуту і прикрас із гробниці Тутанхамона свідчать, що єгипетські майстри користувалися відношенням золотого перерізу при їх створенні.
ПРИГАДАЙТЕ ГОЛОВНЕ
1. Що таке пропорція? Наведіть приклади.
2. Запишіть пропорцію за допомогою букв. Назвіть крайні та середні члени пропорції.
3. Сформулюйте основну властивість пропорції.
4. Запишіть основну властивість пропорції за допомогою букв.
5. Які пропорції вважають взаємно оберненими?
6. Чи зміниться пропорція, якщо в ній поміняти місцями лише середні члени або лише крайні члени?
7. Як знайти невідомий член пропорції?
РОЗВ’ЯЖІТЬ ЗАДАЧІ
552′. Чи є дана рівність пропорцією:
1)12 + 8=15 + 5; 2) 14 – 4 = 20 – 10; 3)4 : 2 = 12 : 6;
4)2 
9 = 6 ∙ 3; 
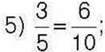6) 8 : 2 = 4 ∙ 1?
Відповідь поясніть.
553′. Прочитайте пропорцію:
1)24 : 8 = 9 : 3 : 2)3 : 2 = 0,15 : 0,1;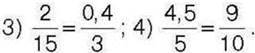 
Назвіть крайні та середні члени пропорції.
554′. Як перевірити, чи є рівність 5:4 = 1,5:1,2 пропорцією, за до помогаю:
1) означення пропорції; 2) основної властивості пропорції?
555′. Чи правильно, що взаємно оберненими є пропорції:
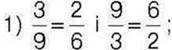2) 3 : 9 = 2 : 6 і 6 : 2 = 9 : З?
556′. Прочитайте справа наліво пропорцію:
1)33 : 11 = 18 : 6; 2) 0,5 : 4 = 1,5 : 12
Якими є дана й отримана пропорції? Чому?
557°. З яких відношень можна скласти пропорцію:
1) 4 : 8; 2)0,2 : 4; 3) 5 : 10;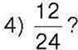 
Відповідь поясніть.
558. З яких відношень можна скласти пропорцію: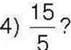 
559°. Чи можна скласти пропорцію з чисел:
1)3,6,9,12; 2)1,2,4,8; 3)0,1,2,3; 4)4,0,5,1?
560°. Складіть пропорцію з чисел: 1) 1, 2, 4, 8; 2) 2, 3, 6, 9; 3) 0,5,1,2,4;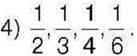 
Відповідь запишіть двома способами.
561°. Складіть пропорцію з чисел:
1)2,4, 6,12;
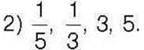
Відповідь запишіть двома способами.
562°. Перевірте, чи виконується основна властивість пропорції:
1)18 : 9 = 30 : 15; 2)2 : 25 = 3 : 37,5;
3) 0,5 : 3 = 10 : 60;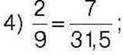 
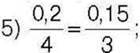
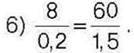
563°. Перевірте, чи виконується основна властивість пропорції:
1)40 : 8 = 15 : 3; 2)5 : 0,4 = 25 : 2;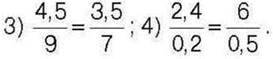 
564°. Складіть пропорцію, використовуючи рівність:
1) 3 ∙ 6 = 2 ∙ 9; 2)5 – 2 = 0,4 – 25;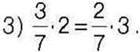 
Скільки пропорцій можна скласти? Відповідь поясніть.
565°. Складіть чотири пропорції, використовуючи рівність:
1)8 ∙ 0,2 = 0,4 ∙ 4;
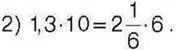
566°. Перевірте двома способами, чи є пропорцією рівність:
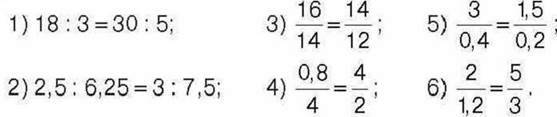
567°. Перевірте двома способами, чи є пропорцією рівність:
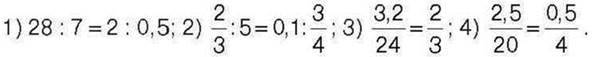
568°. Чи є взаємно оберненими пропорції:
1) 15 : 3 = 2 : 0,4 і 3 : 15 = 0,4 : 2; 2) 15 : 3 = 2 : 0,4 і 15 : 10 = 3 : 2;
Відповідь поясніть.
569°. Чи є взаємно оберненими пропорції:
570°. Складіть пропорцію зі значенням відношень: 1) 3; 2) 0,2. Запишіть пропорції, взаємно обернені зі складеними.
571°. Складіть пропорцію, у якій значення відношень дорівнює 5. Запишіть пропорцію, взаємно обернену зі складеною.
572°. Знайдіть невідомий член пропорції:
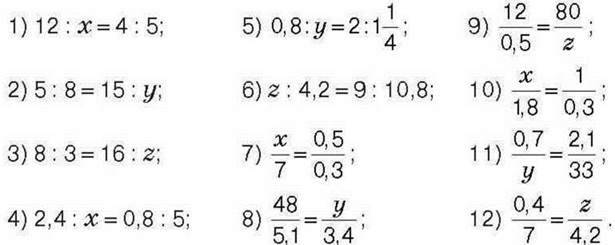
573°. Знайдіть невідомий член пропорції:
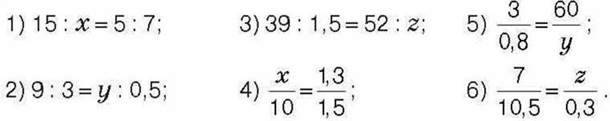
574. Дано пропорцію a : b = c : d. Чи є пропорцією рівність:
1) a : c = b : d; 3)ba : 5b = c : d;
2)d : b = c : a; 4) 4а : 2b=8с : 4d?
Відповідь поясніть.
575. Дано пропорцію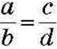 
. Чи є пропорцією рівність:
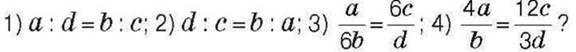
Відповідь поясніть.
576. Крайні члени пропорції дорівнюють 15 і 7, а один із середніх її членів дорівнює 3. Знайдіть інший середній член пропорції. Запишіть усі можливі пропорції з даними членами.
577. Крайні члени пропорції дорівнюють 9 і 24, а один із середніх її членів дорівнює 36. Знайдіть інший середній член пропорції. Запишіть усі можливі пропорції з даними членами.
578. Середні члени пропорції дорівнюють 1,25 і 8, а один із крайніх її членів дорівнює 2,5. Знайдіть інший крайній член пропорції.
579. Середні члени пропорції дорівнюють 4,5 і 4, а один із крайніх її членів дорівнює 12,5. Знайдіть інший крайній член пропорції.
580. Розв’яжіть рівняння:
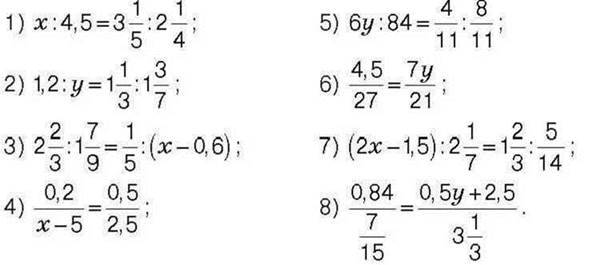
581. Розв’яжіть рівняння:
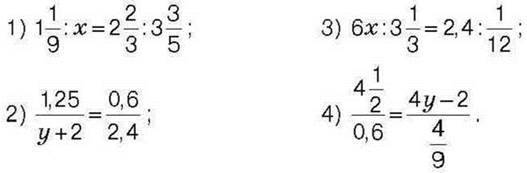
582*. Задумане число подвоїли, а потім зменшили на 6. У результаті вийшло, що отримане число так відноситься до числа 9, як 4 відноситься до 4,5. Яке число задумали?
583*. Відомо, що х : y = 5 : 8 і у : 2 z=16 : 7. Знайдіть z, якщо х = 2,4.
584*. Відомо, що х : у = у : z = 2. Знайдіть відношення х до z.
585*. Знайдіть значення х, якщо:
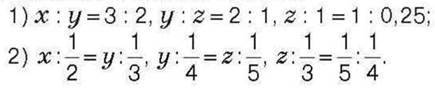
ЗАСТОСУЙТЕ НА ПРАКТИЦІ
586. У 1855 році німецький дослідник золотого перерізу професор А. Цейзинг опублікував книгу “Естетичні дослідження”. У ній учений абсолютизував пропорцію золотого перерізу, оголосивши її універсальною для всіх явищ природи й мистецтва. Слідом за вченими й митцями Стародавнього світу та епохи Відродження він наголошував, наприклад, що пропорції золотого перерізу проявляються у відношенні різних частин обличчя й тіла людини. На малюнках 14-15 ви бачите окремі його розрахунки.
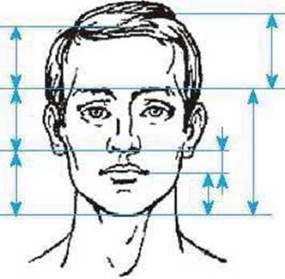
Мал. 14
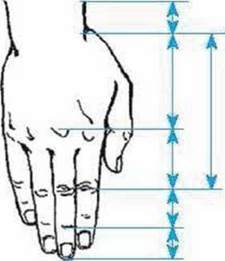
Мал. 15
З’ясуйте, які відрізки на малюнках 14-15 утворюють пропорцію золотого перерізу. Перевірте, виконавши відповідні вимірювання своєї долоні або долоні друга, чи підтверджується пропорційність відрізків, зображених на малюнку 15.
ЗАДАЧІ НА ПОВТОРЕННЯ
587. Знайдіть відношення величин:
1)1,6 мі 20 см; 2) 2 кг і 750 г; 3)1 год і 40 хв.
588. В одному класі навчається менш ніж 40 учнів. На вулиці Смілянській мешкає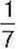 
учнів цього класу, на Різдвяній – 
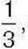на Благовісній – 
і на бульварі Шевченка – решта учнів. Скільки учнів навчається в цьому класі?
(2 votes, average: 4.50 out of 5)
Loading...