Пряма пропорційна залежність
Розділ 3 Відношення і пропорції
§22. Пряма пропорційна залежність
Нехай 1 кг товару коштує 8 грн. Визначимо вартість, наприклад, 2 кг, 4 кг, 5 кг, 0,5 кг, 10 кг цього товару:
Кількість товару, кг | 1 | 2 | 4 | 5 | 0,5 | 10 |
Вартість товару, грн | 8 | 16 | 32 | 40 | 4 | 80 |
Кожного разу маємо різну вартість товару, вона залежить від кількості придбаного товару, а відношення вартості товару до його кількості
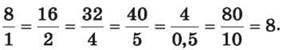
– Дві величини, відношення відповідних значень яких є сталим, називають прямо пропорційними.
З відповідних значень прямо пропорційних величин можна скласти пропорцію, наприклад 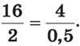
Прямо пропорційними величинами є: вартість товару і його кількість; шлях, пройдений тілом із сталою швидкістю, і час; периметр квадрата і довжина його сторони тощо.
Оскільки 1 кг товару коштує 8 грн, а 2 кг коштують 16 грн, то помічаємо, що вдвічі більшій кількості товару відповідає удвічі більша
– із збільшенням (зменшенням) значень однієї з прямо пропорційних величин у кілька разів значення другої величини збільшується (зменшується) у стільки ж разів.
Задачі на прямо пропорційні величини можна розв’язувати за допомогою пропорції.
Задача. За 2,5 год автомобіль проїхав 170 км. Яку відстань проїде автомобіль за 3,5 год, якщо швидкість його руху є сталою?
Розв’язання. Нехай за 3,5 год автомобіль проїхав х км. Запишемо умову задачі схематично:
2,5 год – 170 км;
3,5 год – х км.
Цю схему розумітимемо так: 2,5 год відповідають 170 км, а 3,5 год відповідають х км. Відстань, яку проїхав автомобіль зі сталою швидкістю, і час є величинами прямо пропорційними: із збільшенням у певну кількість разів часу руху у стільки ж разів збільшиться відстань, яку проїхав автомобіль. Тому можна записати пропорцію: 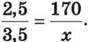
Маємо 2,5х = 170 ∙ 3,5; 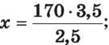
Х = 238 (км).
Відповідь. 238 км.
Які величини називають прямо пропорційними? Наведи приклади прямо пропорційних величин. Яку властивість мають прямо пропорційні величини?
555. (Усно) Значення однієї з двох прямо пропорційних величин збільшилося втричі. Як змінилося значення другої величини?
556. Значення однієї з двох прямо пропорційних величин зменшилося удвічі. Як змінилося значення другої величини?
557. (Усно) За кілька однакових зошитів заплатили 12 грн. Скільки треба заплатити за такі самі зошити, якщо їх буде: 1) у 2 рази більше; 2) у 2 рази менше?
558. (Усно) За кілька однакових блокнотів заплатили 16 грн. Скільки треба заплатити за таку саму кількість блокнотів, кожний з яких:
1) удвічі дорожчий; 2) удвічі дешевший?
559. (Усно) Які з величин є прямо пропорційними:
1) кількість проданих квитків і виручка каси, якщо ціна квитка є сталою;
2) маса сталевого бруска і його об’єм;
3) площа квадрата і довжина його сторони;
4) маса одного цвяха та їх кількість в одному кілограмі;
5) кількість робітників і обсяг виконаної роботи, якщо продуктивність праці всіх робітників є однаковою;
6) довжина і ширина прямокутника, площа якого 100 см2?
560. Які з величин є прямо пропорційними:
1) відстань, яку пройшов турист, і час руху при сталій швидкості;
2) об’єм куба і довжина його ребра;
3) кількість однакових деталей та їх маса присталій масі однієї деталі;
4) кількість робітників, що виконують певну роботу, і час виконання роботи?
561. (Усно) Визначте, у яких таблицях записано прямо пропорційні величини х і у.
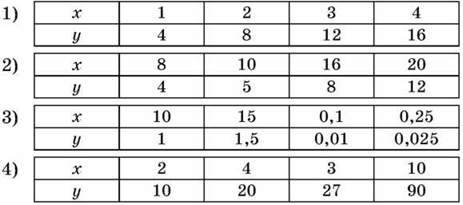
562. Щоб пошити 15 костюмів, витрачають 51 м тканини. Скільки потрібно тканини, щоб пошити 26 таких самих костюмів?
563. За 2 год млин змолов 13 т зерна. Скільки тонн зерна можна змолоти за 6 год, якщо продуктивність млина є сталою?
564. Сталева кулька об’ємом 4 см3 має масу 31,2 г. Яка маса кульки з такої сталі, якщо її об’єм 6 см3?
565. За 1,5 год туристи пройшли 5,1 км. Яку відстань пройдуть туристи за 2,5 год, якщо швидкість їх руху є сталою?
566. За 0,5 л олії заплатили 7,6 грн. Скільки треба заплатити за 1,25 л олії”? Скільки олії можна купити на 22,8 грн?
567. За 0,4 кг ковбаси заплатили 19,2 грн. Скільки треба заплатити за 0,6 кг такої ковбаси? Скільки кілограмів такої ковбаси можна купити на 36 грн?
568. З 10 кг морської води можна видобути 0,7 кг солі. Скільки можна видобути солі з 1 т води?
569. Площа прямокутника 40 см2. Якою стане площа, якщо ширина прямокутника залишиться без змін, а довжину: 1) збільшити в 2,5 раза; 2) зменшити в 5 разів?
570. Об’єм прямокутного паралелепіпеда дорівнює 60 см3. Яким стане об’єм цього паралелепіпеда, якщо його довжину і ширину залишити без змін, а висоту:
1) збільшити вдвічі; 2) зменшити втричі?
571. Маса 10 м3 повітря дорівнює 13 кг. Знайди масу повітря в кімнаті, довжина якої 5 м, ширина – 4 м, а висота – 2,5 м.
572. Залізна кулька, об’єм якої 10 см3, має масу 79 г. Визнач масу куба, ребро якого дорівнює 5 см, який виготовлено з такого самого заліза.
573. За три дні зібрали врожай з 15 % усієї площі поля. Скільки днів треба працювати ще, щоб зібрати врожай з 55 % поля, якщо продуктивність праці є сталою?
574. Розфасували 0,9 ц крупи, що становить 46,8 % усієї крупи, що завезли до магазину. Скільки крупи треба ще розфасувати, щоб вона становила 65 % привезеної крупи?
575. Заповни в зошиті таку таблицю, якщо між величинами а і b існує пряма пропорційність:
А | 9 | 10,2 | 4,2 | 99 |
B | 1,4 | 4,5 | 19,7 |
576. За n кг деякого товару заплатили с грн. Визнач ціну кілограма товару та заповни в зошиті таку таблицю:
N, кг | 7 | 10 | 3 |
C, грн | 31,5 | 67,5 | 54 |
577. Протягом трьох годин 7 насосів викачали 882 відра води. Скільки відер води викачають 4 таких насоси за 5 год?
578. Для восьми коней на 12 днів заготовили 576 кг вівса. Скільки кілограмів вівса слід заготовити для дев’яти коней на 10 днів за такої самої норми споживання?
579. Знайди відношення:
1) 2 хв до 15 с; 2) 300 м до 12 км;
3) 0,2 кг до 300 г; 4) 0,8 м2 до 12 см2.
580. Розв’яжи рівняння: 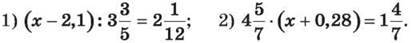
581. 25 % одного числа дорівнюють 40 % другого. Знайдіть відношення цих чисел.
582. Є олівці п’яти кольорів. Скільки різних наборів, що містять лише три олівці різних кольорів, можна з них скласти?