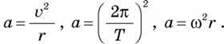Рівномірний рух тіла по колу. Період і частота обертання. Кутова швидкість
КІНЕМАТИКА
Урок № 9
Тема. Рівномірний рух тіла по колу. Період і частота обертання. Кутова швидкість
Мета: формувати знання про переміщення, шлях, швидкість і прискорення, про напрям миттєвої швидкості під час криволінійного руху, про період і частоту обертання тіла; порівняти переміщення, шлях, швидкість під час прямолінійного рівномірного, нерівномірного та криволінійного рухів; розповісти про широке застосування криволінійних рухів у техніці, сільському господарстві.
Тип уроку: урок вивчення нового навчального матеріалу.
Унаочнення:
ХІД УРОКУ
I. Актуалізація опорних знань
Фронтальне опитування про траєкторію, шлях, переміщення, миттєву швидкість прямолінійного руху.
II. Мотивація навчання. Повідомлення теми та завдань уроку
III. Вивчення нового матеріалу
У ході евристичної бесіди учні, слухаючи вчителя, виконують малюнки в зошитах, роблять записи.
Найпростішим видом криволінійного поступального руху тіла є його рух по колу, коли всі точки цього тіла рухаються по однакових колах. Такий рух зустрічається
Почнемо вивчення цього руху з важливої кінематичної величини – миттєвої швидкості. Миттєва швидкість у будь-якій точці криволінійної траєкторії руху тіла напрямлена по дотичній до траєкторії в цій точці.
У цьому можна переконатися, спостерігаючи за роботою на точилі. Якщо притиснути до обертового точильного каменя кінець сталевої дротини, то ви побачите, як розжарені частинки відриваються від каменя у вигляді іскор. Ці частинки летять з тією швидкістю, яку вони мали в момент відривання від каменя. Напрям руху іскор збігається з дотичною до кола в тій точці, де дротина торкається каменя. По дотичній до кола рухаються також бризки від коліс автомобіля, що пробуксовує.
Модуль миттєвої швидкості під час рівномірного руху по колу з плином часу не змінюється. Рівномірним рухом по колу називають рух, під час якого тіло (матеріальна точка) за будь-які рівні проміжки часу проходить однакові відрізки дуг. Прикладами рівномірного руху по колу можна наближено вважати: рух штучних супутників Землі, рух частин, що обертаються в механізмах тощо. Швидкість такого руху матеріальної точки по лінії (колу) за модулем є сталою і в кожній точці кола напрямлена по дотичній.
Положення точки A, що рухається вздовж кола, визначають радіус-вектором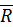 
, проведеним з центра кола O до цієї точки (рис. 1). Модуль радіуса-вектора дорівнює радіусу цього кола R.
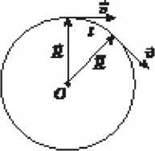
Рис. 1
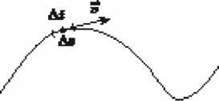
Рис. 2
Швидкість руху тіла по колу (лінійну швидкість) за аналогією з рівномірним прямолінійним рухом можна знайти за формулою:
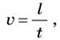
Де l – довжина дуги кола, пройденої матеріальною точкою за час t (рис. 2).
Нехай тіло здійснить один оберт по колу, тоді формула для визначення швидкості набуде вигляду:
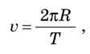
Де T – це час одного оберту по колу радіусом R. Цей час називають періодом обертання. Лінійну швидкість вимірюють у метрах за секунду (м/с).
Набагато частіше в природі й техніці зустрічається обертальний рух тіла, коли нерухомою залишається одна точка або сукупність точок, що лежать на осі обертання. Таким є рух дзиги, колеса нерухомого велосипеда, стрілок годинника тощо. Під час обертання навколо нерухомої осі O різні точки 1, 2, 3 тіла (рис. 3) матимуть різні лінійні швидкості 
1, 2, 3, тому не можна говорити про швидкість тіла. Бажано знайти такі характеристики обертального руху тіла, які були б спільними, однаковими для всіх його точок.
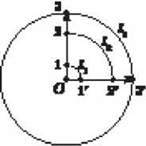
Рис. 3
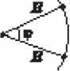
Рис. 4
Як видно з рис. 3, кожна з точок цього диска має свою лінійну швидкість, бо за один і той же час вони проходять відповідно відрізки дуг l1 > l2 > l3. Однаковою для цих точок буде кутова швидкість обертання. Кутова швидкість? точки, що рівномірно рухається по колу, чисельно дорівнює відношенню кута?, на який повертається радіус-вектор, до часу t і залишається сталою:
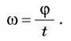
У фізиці кути вимірюють у радіанах (рад). Щоб знайти значення кута ф у радіанах слід провести з його вершини довільну дугу і знайти відношення довжини цієї дуги до радіуса R (рис. 4):
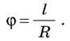
Отже, одиницею вимірювання кутової швидкості є 1 рад/с, що відповідає швидкості точки, яка обертається рівномірно й радіус-вектор якої за 1 с описує кут в 1 рад. А формула для одного оберту по колу набуде вигляду:
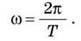
Величину, обернену до періоду обертання, називають частотою обертання і вимірюють кількістю обертів за одиницю часу ([?] = 1/c):
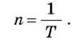
Для довільної кількості обертів частоту обертання знаходять за формулою:
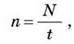
Де N – кількість обертів, t – час обертання тіла.
Після підстановки виразу для частоти обертання маємо:
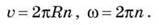
Знайдемо співвідношення лінійної і кутової швидкостей на підставі формули:
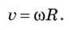
Оскільки лінійна швидкість змінюється за напрямом, то матеріальна точка, що рухається по колу, набуває прискорення. Прискорення тіла, яке рівномірно рухається по колу, у будь-якій його точці є доцентровим, тобто напрямлене по радіусу кола до його центра. У будь-якій точці вектор прискорення перпендикулярний до вектора швидкості. Цю особливість прискорення рівномірного руху по колу зображено на рис. 5.
Чому дорівнює модуль доцентрового прискорення? Числове значення (модуль) прискорення можна легко знайти з рис. 5.
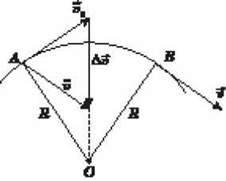
Рис. 5
Трикутник, утворений векторами 0, і?, рівнобедрений, бо = 0. Трикутник OAB на рис. 5 також рівнобедрений, оскільки сторони OA і OB – радіуси кола. Кути при вершинах обох трикутників рівні, бо вони утворені взаємно перпендикулярними сторонами: 0
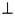OA і 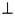OB. Тому трикутники подібні як рівнобедрені з рівними кутами при вершинах. З подібності трикутників випливає пропорційність відповідних сторін:
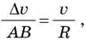
Де і? – модулі швидкості й зміни швидкості під час переходу з точки A в точку B, R – радіус кола. Якщо точки A і B дуже близькі одна до одної, то хорду AB не можна відрізнити від дуги AB. А довжина дуги AB – це шлях, пройдений тілом зі сталою за модулем швидкістю . Він дорівнює T. Тому можна записати:
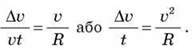
Оскільки інтервал часу t, що розглядається, дуже малий, то?/t – це модуль прискорення. Отже,
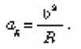
Інші вирази для доцентрового прискорення:
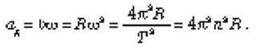
Таким чином, під час рівномірного руху по колу в усіх точках кола доцентрове прискорення за модулем однакове. Проте напрямлене воно завжди по радіусу до центра (рис. 6) так, що напрям прискорення від точки до точки змінюється. Тому рівномірний рух тіла по колу не можна вважати рівноприскореним.
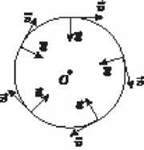
Рис. 6
Будь-який рух по криволінійній траєкторії можна подати як рух по дугах кіл різних радіусів. Одну зі складних траєкторій, за якою рухається тіло, і доцентрове прискорення тіла в різних її точках зображено на рис. 7:
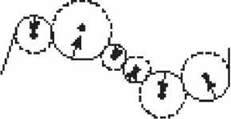
Рис. 7
Отже, у будь-якій точці криволінійної траєкторії тіло рухається з прискоренням, напрямленим до центра того кола, частиною якого є ділянка траєкторії поблизу цієї точки. А модуль прискорення залежить від швидкості тіла та від радіуса відповідного кола.
III. Осмислення об’єктивних зв’язків. Узагальнення знань
1. Фронтальне опитування
– Як напрямлена миттєва швидкість під час криволінійного руху?
– Чим відрізняються зміни швидкості під час криволінійного і прямолінійного рухів?
– Чи може тіло рухатися за криволінійною траєкторією без прискорення?
– Чи можуть збігатися напрями векторів швидкості й прискорення під час криволінійного руху?
– Який зв’язок між криволінійним рухом і рухом по колу?
– Що називають лінійною швидкістю матеріальної точки? Як її виражають через кутову швидкість?
– Як напрямлене прискорення тіла, що рухається по колу зі сталою за модулем швидкістю?
– Чи можна вважати доцентрове прискорення сталим, а рівномірний рух по колу рівноприскореним?
– Якщо під час руху тіла по колу модуль його швидкості змінюється, то чи буде прискорення тіла напрямлене до центра кола?
2. Розв’язування задач (коментовано)
З яким прискоренням рухається автомобіль кільцевою трасою, що має вигляд кола радіусом 100 м, якщо швидкість автомобіля 20 м/c? У скільки разів це прискорення менше від прискорення вільного падіння?
IV. Підсумок уроку
Закінчити речення:
– Я дізнався, що…
– Тепер я можу…
– Отже,…
V. Домашнє завдання
1. Вивчити відповідний параграф підручника, конспект уроку, формули; підготуватися до тематичного оцінювання, захисту презентацій.
2. Розв’язати задачі:
– Скільки обертів ручки криничного коловорота необхідно зробити, щоб підняти відро з водою з криниці глибиною 8 м? Ланцюг, на якому висить відро, намотується на вал радіусом 10 см.
– Знайдіть кутову швидкість і частоту обертання хвилинної стрілки секундоміра зображеної на рисунку, якщо ціна поділки малого циферблата дорівнює 2 хв.
Рис. 8
До конспекту учня
– Рівномірним рухом по колу називається рух по колу зі сталою за модулем швидкістю.
– Основні характеристики рівномірного руху по колу: радіус кола r, період обертання T, частота обертання v, кутова швидкість?.
– Співвідношення між цими величинами:
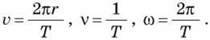
– Миттєва швидкість у певній точці траєкторії напрямлена по дотичній до траєкторії в цій точці, тобто перпендикулярно до радіуса, проведеного з центра кола в цю точку. Під час рівномірного руху по колу прискорення в кожний момент часу напрямлене по радіусу до центра кола. Модуль доцентрового прискорення можна знайти за будь-якою з формул:
(1 votes, average: 5.00 out of 5)
Loading...