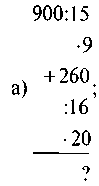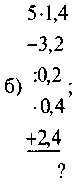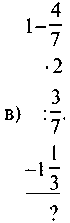Розв’язування текстових задач на відсотки (суміші, сплави, відсотковий вміст)
Урок № 48
Тема. Розв’язування текстових задач на відсотки (суміші, сплави, відсотковий вміст)
Мета: вдосконалити вміння учнів розв’язувати текстові задачі на відсотки та застосовувати їх для розв’язування задач більш високого рівня складності (суміші, сплави).
Тип уроку: застосування знань, умінь та навичок.
Хід уроку
І. Перевірка домашнього завдання. Актуалізація опорних знань
1. Учні заповнюють аркуші контролю впродовж 3-5 хвилин (в аркуші контролю вписують тільки відповіді на запитання, що належать до розв’язаних
2. Фронтальна робота.
Усні вправи
1) Обчисліть: |
|
|
|
2) Знайдіть відношення чисел: 12 до 6; 12 до 36; 9 до 4. Що показує кожне з цих відношень?
3) Які числа можна підставити замість квадратиків, щоб пропорції були правильними? а) ? : 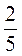 =
= 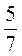 : ?; б)
: ?; б) 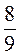 : ? = ? : 1.
: ? = ? : 1.
4) Яке з поданих розв’язань відповідає умові задачі: “До магазину завезли 460 кг картоплі. Першого дня було продано 35 %
А) 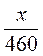 =
= 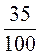 ; б) х = 460 : 0,35; в) х = 460 –
; б) х = 460 : 0,35; в) х = 460 – 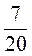 ; г) 460 : 100 = 4,6(кг) 1 %; х = 4,6 –
; г) 460 : 100 = 4,6(кг) 1 %; х = 4,6 – 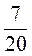 .
.
3. Індивідуально. Щоб активізувати роботу “сильних” учнів, пропонуємо їм індивідуальні завдання з теми.
Картка 1 Додали три числа. Перше становить 25 %, друге 35 % від суми. Які числа додали, якщо третє число на 2,1 більше від другого? |
Картка 2 60 % земельної ділянки засіяли пшеницею, решту вівсом. Яку площу засіяли пшеницею, яку вівсом, якщо пшеницею засіяли на 114 га більше, ніж вівсом? |
II. Застосування вмінь
@ Фактично питання розв’язування задач на відсотки, яке винесено на державну підсумкову атестацію в 9 класі, ретельно опрацьовується лише в 5-6 класах (й епізодично зустрічається в задачах на уроках алгебри та геометрії у 7-9 класах). Тому дуже важливо зараз сформувати сталі, тверді навички розв’язування задач на відсотки, а також, якщо клас готовий до цього, похідних від них задач: задачі на суміші, сплави, відсотковий вміст (що передбачають і складання рівнянь у вигляді пропорцій). Тому на цьому уроці можна запропонувати до розв’язування такі або подібні до них задачі.
1. Сплав міді з оловом масою 12 кг містить 45 % міді. Скільки кілограмів чистого олова треба добавити до сплаву, щоб дістати новий сплав, який містить 40 % міді?
2. У залізній руді на 7 частин заліза припадає 3 частини домішок. Скільки тонн домішок у руді, яка містить 73,5 тонн заліза?
3. Сплав складається з міді (50 %), цинку (40 %) і алюмінію (10 %). Скільки треба взяти металів, щоб дістати 35 кг сплаву?
4. Сплав складається з алюмінію (83 %), цинку (10%) і олова (7 %).Чому дорівнює маса сплаву, в якому цинку на 2,7 кг більше, Ніж олова?
5. Маємо 735 г 16 % розчину йоду у спирті. Треба дістати 10 % розчин йоду. Скільки грамів спирту треба долити для цього у даний розчин?
Також бажано розв’язати інші текстові задачі.
1. З 1,6 га землі, що становить 8% площі всього поля, зібрали 48 ц пшениці. Скільки центнерів пшениці зібрали з усього поля, якщо врожайність на всіх його ділянках однакова?
2. Фермер засіяв соняшником 1,8 га. Це на 20% більше, ніж торік. Яку площу фермер засіяв соняшником торік?
III. Підсумки уроку
У розчині міститься 42 кг солі. Яка маса розчину, якщо солі в ньому 60 %?
А) 42 – 6 = 252 (кг); б) 42 : 6 = 7 (кг); в) 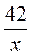 =
= 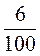 ; х =
; х = 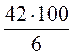 = 700 кг; г) 42 : 0,06 = 700 (кг).
= 700 кг; г) 42 : 0,06 = 700 (кг).
IV. Домашнє завдання
Повторіть теми:
1) “Основна властивість пропорції”;
2) “Прямо і обернено пропорційні величини”.
Розв’яжіть задачі:
1. У воді розчинили 180 г солі і одержали 12%-ий розчин солі. Скільки грамів води використали для приготування розчину?
2. Три трактори зорали поле. Перший трактор зорав 40 % усього поля, другий – 80 % того, що зорав перший. А третій – решту 14 га. Скільки гектарів поля зорав другий трактор?
3. Один учень стрибнув у довжину на 2,4 м, а стрибок другого був на 15 % довший. Яка довжина стрибка другого учня?
4. За 36 робочих днів бригада лісорубів у складі 30 чоловік заготовила 1944 м3 дров. Продуктивність праці всіх лісорубів однакова. Скільки дров заготовить бригада із 24 чоловік за 50 днів при такій же продуктивності праці?
5. Розв’яжіть рівняння: а) 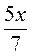 =
= 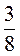 ; б)
; б) 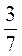 =
= 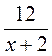 .
.