Сума та різниця кубів
Урок № 47
Тема. Сума та різниця кубів
Мета: домогтися свідомого засвоєння змісту формул (a ± b)(a2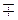 
ab + b2) = a3 ± b3 та виробити базові вміння застосовувати ці формули для перетворень відповідних цілих виразів у багаточлен стандартного вигляду.
Тип уроку: засвоєння знань.
Хід уроку
I. Організаційний момент
@ Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.
II. Перевірка домашнього завдання
@ Щоб перевірити якість виконання домашнього завдання, збираємо зошити. Оскільки виконання
III. Формулювання мети й завдань уроку
@ Учитель знову нагадує учням (або спонукає їх до самостійної роботи щодо усвідомлення місця розділу, що вивчається: “Формули скороченого множення” з теми “Багаточлени та дії з ними”) і формулює мету уроку: продовжити роботу з вивчення формул скороченого множення; виробити вміння застосовувати нові знання для перетворення цілих виразів у багаточлен
IV. Актуалізація опорних знань
Виконання усних вправ
1. Прочитайте вираз:
1) (а – b);
2) (а + b);
3) (а – b)2;
4) (а + b)2;
5) а2 – 2аb + b2;
6) а2 + 2аb + b2;
7) а3 – b3;
8) а3 + b3;
9) а2 – аb + b2;
10) а2 + аb + b2.
2. Подайте у вигляді багаточлена:
(a + b)2; (a – b)2; (а + b)(а – b); (а + b)(с + d).
V. Вивчення нового матеріалу
1. Робота з випереджальним домашнім завданням.
Завдання 1. Використовуючи правило множення багаточлена на багаточлен, виконайте множення багаточленів. Утворені вирази (багаточлени) зведіть до стандартного вигляду:
1) (а – b)(а2 + аb + b2);
2) (а + b)(а2 – аb + b2);
3) (с – d)(с2 + сd + d2);
4) (с + d)(с2 – сd + d2);
5) (m – 1)(m2 + m + 1);
6) (m + 1)(m2 – m + 1).
Завдання 2. Випишіть умову кожного із завдань та багаточлен стандартного вигляду, що йому тотожно дорівнює, і запишіть відповідні рівності.
Прочитайте ці рівності, використовуючи терміни “сума”, “добуток”, “різниця”, “квадрат”.
Порівняйте утворені рівності та зробіть висновок.
2. Засвоєння знань.
@ Після виконаної роботи (див. п. 1) традиційно вчитель разом з учнями формулює спочатку у вигляді тотожності, а потім за допомогою слів формули, які мають назву “сума та різниця кубів” (двох виразів). У конспектах учні можуть зробити відповідні записи.
Конспект 14 |
Сума й різниця кубів |
(добуток) |
1) (а + b) • (а2 – аb + b2) = а3 + b3 |
(суми двох виразів) на (їх неповний квадрат різниці) дорівнює (сумі кубів цих двох виразів) |
(добуток) |
2) (а – b) • (а2 + аb + b2) = а3 – b3 |
(різниці двох виразів) на (їх неповний квадрат суми) дорівнює (різниці кубів цих двох виразів) |
При цьому слід звернути увагу, що виділені слова допомагають краще запам’ятати зміст формул (бо часто учні, не задумуючись над змістом, припускаються в цих місцях помилок).
VI. Засвоєння вмінь
Виконання усних вправ
1. Назвіть неповний квадрат різниці виразів:
1) x i y; 2) c i d; 3) р i 1; 4) 2 i c.
2. Назвіть неповний квадрат суми виразів:
1) m і n; 2) р і q; 3) а і 1; 4) 3 і х.
Виконання письмових вправ
1. Спростіть вирази:
1) (а – b)(а2 + аb + b2);
2) (с + d)(с2 – сd + d2);
3) (m – n)(m2 + mn + n2);
4) (х + у)(х2 – ху + у2).
2. Перетворіть у багаточлен стандартного вигляду:
1) (х2 – 1)(х4 + х2 + 1) + 1; 2)(а2 + b 2)(а2 – а2b2 + b4) – а6 – b6;
3) (а + 2)(а2 – 2а + 4) – (а – 2)(а2 + 2а + 4);
4) (х + 2)(х2 – 2х + 4) – х(х – 3)(х + 3);
5) (7а2 – 1)(49а4 + 7а2 + 1) – 4а2(5а2 – 1)2 + (5а2 – 3)(3 – 8а2);
6*) (a + 1)(а – 1)(а2 – а + 1)(а2 + а + 1)(а6 + 1)(а12 + 1)(а24 + 1).
* Під час виконання цього завдання бажано домогтися від учнів розуміння того, що дії кожного учня при перетворенні цілих виразів повинні бути не спонтанними, а свідомими, тобто підкорятись певній послідовності:
1) Встановлюємо порядок виконання дій, визначений умовою задачі.
2) Шукаємо у виразі добутки, які можна перетворити у багаточлен за формулами (не забуваємо про можливість застосування законів множення та властивостей степеня).
3) Якщо добутки багаточленів не відповідають жодній з формул, використовуємо алгоритм множення багаточленів.
4) Після виконання множення використовуємо інші дії з багаточленами (додавання, віднімання, зведення подібних доданків).
3. Розв’яжіть рівняння:
1) (х – 2)(х2 + 2х + 4) = х3 + 4х;
2) (у2 – 3у + 9)(у + 3) = 6у + у3;
3) (4 – 5х)(16 + 20х) + 25х2 + 5х(5х – 2)(5х + 2) = 4;
4) 
.
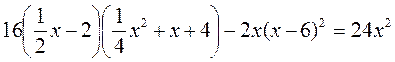4* (додатково). Логічні вправи (на повторення). Яке число або вираз пропущені?
А) 3а + 4 | 9а2 + 24а + 16 | Б) сп+3 | Сп-5 | С8 |
12аb7 | ? | 5а9b16 | A8b20 | ? |
VII. Підсумки уроку
Заповніть пропуски, щоб записи стали правильними:
1) …суми двох виразів на неповний квадрат їх… дорівнює… кубів цих двох виразів;
2) (… – 1)(a2 … a… 1) = a3 – …
VIII. Домашнє завдання
№ 1. Спростіть вираз:
1) (х – 2)(х2 + 2x + 4) – (1 – х)(х2 + x + l);
2) (х – 3)(х2 + 3х + 9) – (х + 1)(х – 1)(х – 2);
3) а(а – 3)(а + 3) – (а + 2)(а2 – 2а + 4);
4) (3а2 + 1)(9а4 – 3а2 + 1) – 3а2(2а2 + 1)2 + (5а2 – 1)(2 – 3а2).
№ 2. Розв’яжіть рівняння:
1) (2 – 3х)(4 + 6х + 9х2) + 3х(3х – 1)(3х + 1) = х;
2) 
.
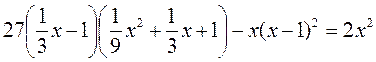№ 3. Випереджальне домашнє завдання.
1) Користуючись відповідним пунктом підручника та записами в зошиті, повторіть зміст понять та алгоритмів:
– розкладання на множники;
– винесення спільного множника за дужки;
– розкладання багаточленів на множники способом групування.
2) Випишіть у стовпчик усі вивчені формули скороченого множення.
Чи є дані рівності тотожностями? Запишіть ці тотожності, помінявши місцями ліву та праву частину кожної рівності.
(1 votes, average: 5.00 out of 5)
Loading...