Множення одночлена на багаточлен
Урок № 34
Тема. Множення одночлена на багаточлен
Мета: спираючись на знання розподільної властивості множення, сформулювати загальний алгоритм множення одночлена на багаточлен; виробити вміння застосовувати сформульоване правило (алгоритм) для перетворення добутку одночлена у багаточлен стандартного вигляду; вдосконалити вміння перетворювати багаточлени.
Тип уроку: засвоєння знань, умінь та навичок.
Хід уроку
I. Перевірка домашнього завдання
Перевірку домашнього завдання можна організувати, зібравши зошити й оцінивши
II. Робота з випереджальним домашнім завданням
@ Учні самостійно виконують завдання, запропоноване вчителем, а після виконання перевіряють, обговорюють та корегують виконання завдань.
№ 1. Серед запропонованих виразів виберіть: 1) одночлени; 2) багаточлени; 3) тотожно рівні вирази:
A; b + c; ab + ac; b + c + d; ab + ac + ad; ab + c + d; ab + c.
№ 2. Прочитайте утворені в п. 3) тотожності, використовуючи слова “одночлен”, “багаточлен”, “член багаточлена”, “добуток”,
ІІІ. Засвоєння знань
@ Після виконання перевірки випереджального домашнього завдання і за умови, що учні мають навички перетворень із використанням розподільної властивості множення, вироблення яких почалося ще в 5 класі, формулювання загального алгоритму перетворення добутку одночлена на багаточлен у багаточлен стандартного вигляду не викликає в учнів жодних труднощів. Але, щоб не мати труднощів у формулюванні наступних алгоритмів, зокрема множення багаточлена на багаточлен, формул скороченого множення тощо, бажано акцентувати увагу учнів на тому, що у формулах, відомих учням ще з початкових класів, наприклад
А(b + с) = ab + ас,
А, b, с можуть бути не тільки числами, а й виразами, в тому числі одночленами, степенями та добутками одночленів, багаточленами, їх степенями тощо, тобто формула задає тільки “форму” виразів. (Щоб це твердження було більш наочним, можна запропонувати учням саме такого вигляду запис сформульованого алгоритму:
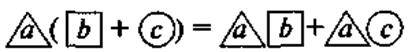
IV. Засвоєння вмінь
@ Оскільки сформульований на уроці алгоритм множення одночлена на багаточлен має широкий спектр застосування, бажано на уроці розв’язати різнопланові вправи на застосування цього алгоритму.
Виконання усних вправ
1. Спростіть вираз: х5 • х2; аа2; -2b • (-8b); хn • хn+3; 4а2 • (-8n3).
2. Назвіть члени багаточлена: а + 1; а2 – 2а; х2 + х – 4.
3. Розкрийте дужки: (5х + 2) • 7; 8(х + 3); 12(10 – 3b).
4. Виконайте множення:
1) а(а + 1);
2) а(а2 – 2);
3) х(х2 + х – 4);
4) (а + 4)а;
5) (b + 2a)b;
6) (у2 + 4у + 4)у.
Виконання письмових вправ
1. Виконайте множення:
1) -3а(а2 + 2ab – 5b);
2) (4y2 – 2у5 + 16)(-2,5у);
3) 0,3mn(2mn2 – 4m2n + 3mn);
4) 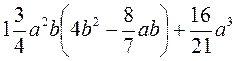 ;
;
5*) xn+2(xn+3 + 2хn + х2n-1).
2. Перетворіть на багаточлен вираз:
1) 2,4(5х – 10) – 5(х + 1) – 3(1 – 3х);
2) 0,3х2(х2 – 3х + 2) – 0,6х(2х3 + 6х2 – 4х);
3*) 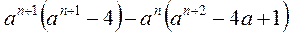 .
.
3. Доведіть, що значення виразу 2×2(1 + 3х) – x(4×2 – 2) – 2(х2 + х3 + х – 3) не залежить від значення х.
4. Розв’яжіть рівняння:
1) 2х(3х – 2) – 3(х2 – 4х) = 3х(х – 7) + 2;
2) 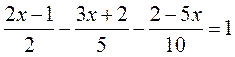 .
.
5. При якому значенні змінної подвоєне значення тричлена
-2х3 + 3х2 + 5х дорівнює різниці виразів х2(1 – 3х) та х3 – 5×2 – 5?
6. Розв’яжіть задачу. Шлях від села до міста легковий автомобіль долає за 5 годин, а вантажівка – за 7 годин. Яку швидкість має легковий автомобіль, а яку – вантажівка, якщо швидкість легкового автомобіля на 20 км/год. більша від швидкості вантажівки.
7*. Логічна вправа.
Підземна частина рослини | Корінь |
5а2(а – 3) – а(а2 + 1) | ? |
V. Підсумки уроку
Учитель пропонує учням завдання на систематизацію (знайти місце теми серед основних видів завдань, що їх розв’язує алгебра).
Завдання: спираючись на розв’язані в класі вправи, побудуйте логічний ланцюжок із записаних понять. Поясніть свою думку.
Розв’язування задач; множення одночлена на багаточлен; багаточлен стандартного вигляду; перетворення цілих виразів; розв’язування рівнянь; складання рівнянь.
(Мається на увазі:
1) множення одночлена на багаточлен як один з видів перетворення цілих виразів
V
2) приводить до багаточлена стандартного вигляду
V
3) допомагає (є засобом) складати та розв’язувати рівняння
V
4) які є засобом розв’язування задач.)
VI. Домашнє завдання
Спираючись на алгоритм перетворення добутку одночлена на багаточлен та суми й різниці багаточленів у багаточлен стандартного вигляду, виконайте завдання.
№ 1. Спростіть вираз та обчисліть його значення:
1) x(2x – 1) – 3х(3 – 5х), якщо х = -2;
2) 2аb(3а2 – 2b2) – 3аb(аb2 – а2), якщо а = 1; b = -2.
№ 2. При якому значенні змінної значення виразу 1,5х2 – 2х, збільшене у 4 рази, на 6 менше від значення виразу 3(2х2 + 5) ?
№ 3. Випереджальне домашнє завдання.* Використовуючи текст підручника та зміст матеріалу уроку, дайте відповідь на запитання:
1) Що означають букви а, b, с у записі:
A(b + c) = ab + ac? (1)
2) Чи буде рівність вигляду (1) правильною, якщо замість а підставити:
А) х2; б) 3х2; в) х + 2; г) х + у?
Запишіть утворені рівності.
* Замість попереднього завдання можна запропонувати:
№ 3 а) Розгляньте рисунок.
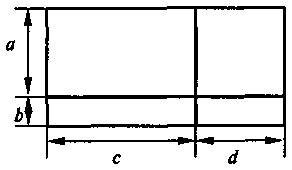
Запишіть у вигляді виразу площу найбільшого прямокутника різними способами. Якими будуть значення всіх записаних вами виразів?
Або
№ 3 б) Обчисліть значення виразів та знайдіть серед них рівні:
1) 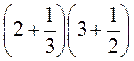 ;
;
2) 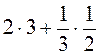 ;
;
3) 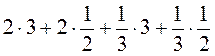 .
.
Прочитайте записану рівність, використовуючи слова “сума”, “добуток”, “доданок”.
