ВАЖІЛЬ. УМОВА РІВНОВАГИ ВАЖЕЛЯ
Розділ 4 МЕХАНІЧНА РОБОТА ТА ЕНЕРІЯ
& 56. ВАЖІЛЬ. УМОВА РІВНОВАГИ ВАЖЕЛЯ
Важіль. Відомо, якщо необхідно пересунути чи підняти (підважити) деяке важке тіло (кам’яну брилу, колоду, шафу), то використовують міцну жердину, лом або палку. Якщо потрібно пересунути важкий камінь, то один кінець жердини підсовують під нього, а за другий кінець жердину піднімають. Жердина починає обертатися навколо кінця – точка О, що спирається на землю і, докладаючи порівняно невеликих зусиль, можна припідняти й перекотити камінь (мал. 4.19). Це і є найпростіший
Важелем називають тверде тіло, що має нерухому вісь обертання.
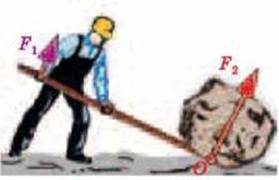
Мал. 4.19

Мал. 4.20
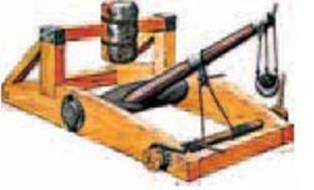
Мал. 4.21

Мал. 4.22
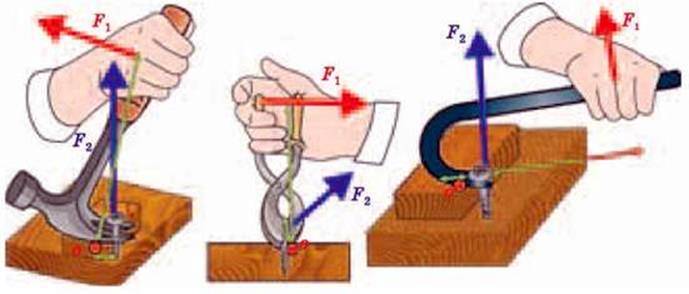
Мал. 2.23
Важелі використовували ще стародавні будівельники. За допомогою важелів піднімали кам’яні блоки під час будівництва єгипетських пірамід (мал. 4.20). їх використовували у військових машинах для метання каміння (мал. 4.21), у судноплавстві (мал. 4.22).
Із застосуванням важелів ми зустрічаємось повсякчасно. Гайковий ключ,
Залежно від того, як діють сили і де розташована точка опори (вісь обертання) важеля, їх поділяють на кілька типів. Найчастіше маємо справу із важелями трьох типів. Якщо точка опори важеля О розташована між точками прикладання сил, то такий важіль називають важелем першого роду (мал. 4.24). Важелями першого роду є, наприклад, щипці, ножиці, залізничний шлагбаум. У цьому випадку сила з боку навантаження і сила, прикладена для врівноваження важеля, мають однаковий напрямок.
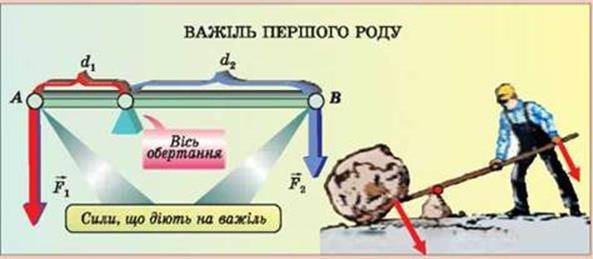
Мал. 4.24
Якщо вісь обертання розташована на одному з кінців важеля, точка прикладання сили F1 – на іншому, а точка прикладання навантаження F2 розташована між ними (точка А), то такий важіль називають важелем другого роду (мал. 4.25). У цьому випадку сили діють у протилежних напрямках. Гайкові ключі, стріли підіймальних кранів, тачки для перевезення будівельних матеріалів, педалі велосипеда – це важелі другого роду. Такі важелі дають виграш у силі – прикладена сила буде меншою за навантаження, прикладене до важеля.
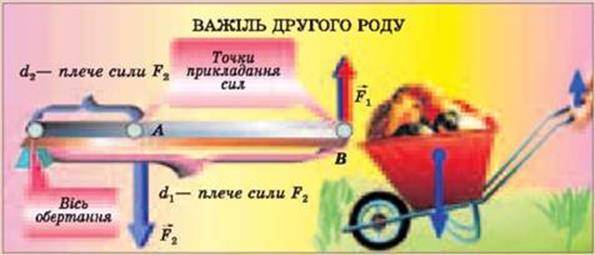
Мал. 4.25
Якщо вісь обертання розташована на одному з кінців важеля, точка прикладання навантаження F2 – на іншому кінці, а точка прикладання сили F1 розташована між ними, то такий важіль називають важелем третього роду. У цьому випадку сили теж діють у протилежних напрямках. Проте, використовуючи такі важелі, завжди програють у силі. Прикладами важелів третього роду є пінцет, рука, нога людини (мал. 4.26, а, б).
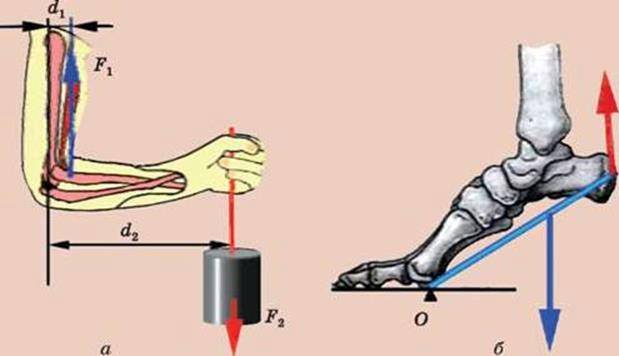
Мал. 4.26
Постають питання: чому, щоб відкрутити туго затягнуту гайку, потрібен гайковий ключ? Чому ручки дверей кріплять так, як показано на мал. 4.27, а, а не так як на мал. 4.27, б? Чому, щоб зсунути з місця важкий камінь, використовують лом або довгу жердину? Для відповіді на них слід з’ясувати особливості дії сил на тіла, що можуть обертатися навколо закріпленої осі або точки опори.
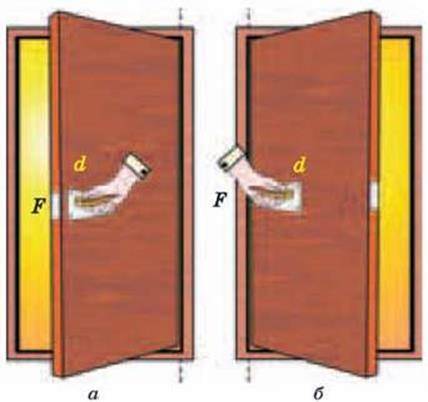
Мал. 4.27
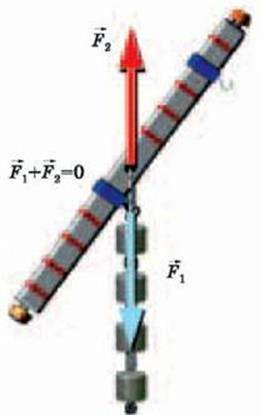
Мал. 4.28
Момент сили. Скористаємось спеціальною лінійкою-важелем з отвором посередині, в який можна вставити стрижень. Закріпивши стрижень у штативі, ми отримаємо модель тіла, що може вільно обертатися навколо закріпленої осі, – важіль. Урівноважимо лінійку так, щоб вона зберігала горизонтальне положення. Підвісимо до неї на відстані l1 = 5 см чотири тягарці, кожен масою 100 г. Тягарці діють з одного боку на лінійку із силоюF1, яка приблизно дорівнює 4 Н, направленою вертикально вниз. Лінійка повернеться і займе таке положення, що лінія дії сили пройде через вісь обертання лінійки. Крім того, на лінійку діє сила F2 з боку осі, направлена угору уздовж цієї прямої. Рівнодійна цих сил дорівнює нулю (F1 – F2 = 0), тому лінійка перебуває в рівновазі (мал. 4.28).
Використавши динамометр, визначимо силу, яку потрібно прикласти до іншого кінця лінійки, щоб повернути її в попереднє положення. Виявляється, на відстані l2 = 20 см від осі потрібно подіяти силою F2 = 1 Н, у чотири рази меншою ніж F1 = 4 Н (мал. 4.29, а).
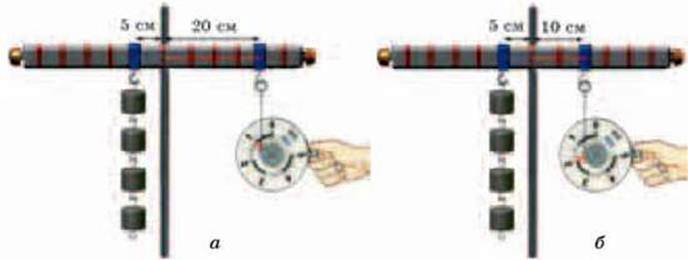
Мал. 4.29
Пересуваючи гачок, до якого причеплено динамометр, уздовж лінійки-важеля, з’ясовуємо, що на відстані l2 = 10 см потрібно прикласти силу F2 = 2 Н (у два рази меншу за силу, з якою діють тягарці) (мал. 4.29, б). Якщо відстані від осі l2 = l1 = 5 см, то динамометр покаже силу F2 = F = 4 Н (мал. 4.30). Отже, результат дії сили F2, яку необхідно прикласти, щоб урівноважити лінійку, залежить від того, на якій відстані від осі на важелі розташована точка її прикладання. Чим далі від осі точка прикладання сили (гачок, до якого причеплено динамометр), тим істотнішим буде її вплив на важіль.
Проте не поспішаємо з остаточним висновком. Змінюватимемо напрямок дії сили, точка прикладання якої знаходиться на відстані l2 = 20 см від осі лінійки. Як бачимо, покази динамометра збільшуються. Скориставшись кутником і виконавши прості вимірювання, можна переконатися, що коли найкоротша відстань (довжина перпендикуляра, проведеного від осі обертання до лінії, уздовж якої діє сила) дорівнюватиме l2 = 10 см, для утримання лінійки необхідно прикласти силу
F0 = 2 Н, а при зменшенні відстані до l2 = l1 = 5 см – F2 = = 4 Н (мал. 4.31).
Найкоротшу відстань від осі обертання до напрямку дії сили називають плечем сили.
Отже, результат дії сили на тіло, що має закріплену вісь обертання, тим більший, чим більше її значення та довжина перпендикуляра, опущеного з осі обертання на напрямок дії цієї сили, – плеча сили. Інакше, результат дії сили на важіль (тіло, що має закріплену вісь обертання) визначається добутком прикладеної сили F на її плече l.
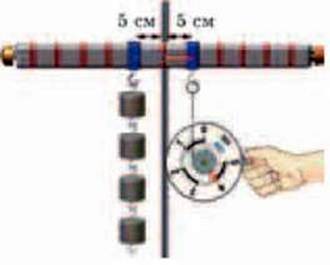
Мал. 4.30
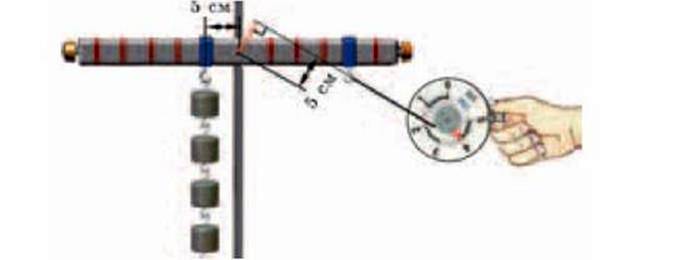
Мал. 4.31
Фізичну величину, яка дорівнює добутку сили на її плече, називають моментом сили і позначають літерою М:
М = Fl.
Результат дії сили на тіло, яке може обертатися навколо закріпленої осі, визначається моментом сили.
Оскільки момент сили визначається добутком сили на її плече, одиницею моменту сили у СІ є 1 Н ∙ м. Такий момент створює сила в 1 Н, якщо її плече становить 1 м.
Для тіла, яке може обертатися, саме момент сили зумовлює особливості його обертального руху і рівноваги.
Зверніть увагу!
Діючи на лінійку за допомогою динамометра, ми обертали її за годинниковою стрілкою. Прикріплені до лінійки тягарці обертали лінійку проти руху годинникової стрілки. Момент сили, який спричиняє (чи може спричинити) обертання тіла за годинниковою стрілкою, прийнято вважати додатним, а той, який обертає тіло проти годинникової стрілки, – від’ємним.
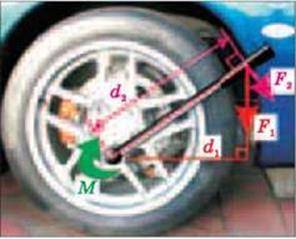
Мал. 4.32
Більшість гвинтів і гайок виготовляють так, що вони закручуються за годинниковою стрілкою (мають праву нарізку). Для їх закручування необхідно, щоб момент сили, яка діє на гайку (гвинт, болт), був додатний і, навпаки, для відкручування – від’ємний.
Якщо необхідно сильніше закрутити гайку (або потрібно відкрутити туго затягнуту гайку), ключ беруть із довшою ручкою і прикладають силу перпендикулярно до неї. У цьому випадку для створення такого самого моменту сили М потрібно прикласти меншу силу (мал. 4.32).
Використана нами лінійка-важіль – це модель найпростішого важеля. її вісь обертання є точкою опори (точка О) важеля. Коли прикладена до лівої частини важеля (див. мал. 4.29) сила становила F1 = 4 Н, а її плече l1 = 5 см, момент цієї сили М1 = F1l1 = 4 Н ∙ 0,05 м = 0,2 Н ∙ м спричинив обертання важеля проти годинникової стрілки. Щоб повернути важіль у попередній стан рівноваги, до її правої частини приклали силу F2 = 1 Н так, що плече сили становило l2 = 20 см. Момент цієї сили М2 = F2l2 =1 Н ∙ 0,2 м = 0,2 Н ∙ м, такий самий за значенням, спричинив обертання лінійки за годинниковою стрілкою. Коли плече сили, з якою діяв на важіль динамометр, зменшилося удвічі (10 см), для встановлення рівноваги необхідно було прикласти удвічі більшу силу – 2 Н. Але момент сили залишився таким самим – 0,2 Н. Отже, можна зробити висновок щодо умови рівноваги важеля: важіль перебуває у рівновазі, якщо момент сили, який спричинює його обертання за годинниковою стрілкою, чисельно дорівнює моменту сили, який обертає його проти годинникової стрілки: М1 = М2.
Урахувавши, що момент сили F1 який спричинює обертання проти годинникової стрілки, від’ємний, а момент сили F2, що зумовив обертання важеля за годинниковою стрілкою, – додатний, умову рівноваги важеля можна сформулювати так: важіль перебуває у рівновазі, якщо алгебраїчна сума моментів сил, що діють на нього, дорівнює 0: М1 + М2 = 0.

Мал. 4.33
Це правило стосується і випадків рівноваги важеля, якщо на кожне з плечей діє кілька сил. Можна змінювати плечі сил, що діють на важіль, значення сил, але в усіх випадках важіль перебуватиме у рівновазі, якщо сума моментів сил, які обертають його проти годинникової стрілки, дорівнює сумі моментів сил, які обертають його за годинниковою стрілкою.
Урахувавши, що момент сили – це добуток сили на її плече, рівність М1 = М2 можна записати у вигляді F1l1 = F2l2. З останньої рівності випливає, що 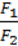 =
= 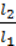 .
.
Важіль перебуває у рівновазі, коли сили, які діють на нього і намагаються обертати важіль у протилежних напрямках, обернено пропорційні до плечей цих сил.
Правило рівноваги важеля було встановлене Архімедом. За легендою, Архімеду належить вислів: “Дайте мені точку опори і я переверну Землю” (мал. 4.33).
Чим більше плече сили, тим меншу силу потрібно прикласти, щоб урівноважити важіль. За допомогою важеля можна дістати виграш у силі в стільки разів, у скільки разів плече сили, яка прикладається, більше за плече сили, яка діє з боку вантажу:
F1 = F2 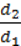 .
.
ЗАПИТАННЯ ТА ЗАВДАННЯ
1. Що називають важелем?
2. Від чого залежить результат дії сили на тіло, яке має закріплену вісь обертання?
3. Що називають плечем сили?
4. Що таке момент сили?
5. Який момент сили прийнято вважати додатним? Від’ємним?
6. За яких умов важіль може перебувати у рівновазі?
7. Кожен тягарець діє на лінійку, підвішену на осі О із силою 1 Н. Яку силу показуватиме динамометр (мал. 4.34)?
8. На мал. 4.35 показано тіло із закріпленою віссю обертання, на яке діють кілька сил. Перемалюйте малюнок у зошит і позначте на ньому плечі цих сил.
9. Розповідаючи про важіль, дівчинка намалювала схему важеля в рівновазі (мал. 4.36). Яку помилку допущено на малюнку?
10. Яку силу треба прикласти до важеля в точці А, щоб зрівноважити вагу вантажу (мал. 4.37)?
11. На мал. 4.38 показано відстані уздовж стріли баштового крана і допустимі вантажі, які можна піднімати? Чому чим на більшу відстань необхідно перемістити вантаж

Мал. 4.34
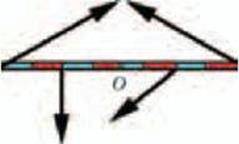
Мал. 4.35
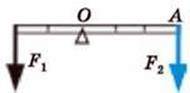
Мал. 4.36
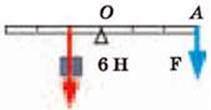
Мал. 4.37
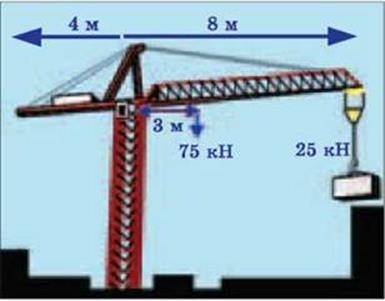
Мал. 4.38
Уздовж стріли баштового крана, тим меншою має бути вага вантажу? Яка роль тягаря, закріпленого на протилежній від гака лівій частині стріли крана? Який момент сили у 25 кН, з якою вантаж діє на стрілу? Якою має бути вага тягаря на протилежній від гака лівій частині стріли, щоб створюваний ним момент сили дорівнював моменту сили, створюваному вантажем?
ЛАБОРАТОРНА РОБОТА № 11
Вивчення умови рівноваги важеля
Завдання. Перевірити умови, за яких важіль може перебувати в рівновазі.
Обладнання: модель важеля; штатив; лінійка; набір тягарців; динамометр.
Підготовка до проведення експерименту
1. Закріпіть важіль (лінійку) на штативі і врівноважте його плечі так, щоб він перебував у горизонтальному положенні.
2. Підготуйте таблицю для занесення результатів вимірювань
І обчислень:
Номер Досліду | F1, Н | D1, м | F2, Н | D2, м | M1, H ∙ м | М2, Н ∙ м |
1 | ||||||
2 | ||||||
3 |
Проведення експерименту
1. Притримуючи важіль, підвісьте з одного його боку на відстані кількох сантиметрів від осі декілька тягарців, зачепивши їх один за один (мал. 4.39).
2. Підвісьте 1-2 зчеплені тягарці на інший від осі бік важеля. Притримуючи важіль, пересувайте уздовж нього точку кріплення тягарців так, щоб відновилися рівноваги важеля.
3. Вважаючи, що кожен тягарець діє на важіль із силою 1 Н, визначте сили, які діють на важіль та їх плечі.
4. Обчисліть моменти сил, які спричиняють обертання важеля за і проти годинникової стрілки. Порівняйте їх значення.

Мал. 4.39
5. Повторіть досліди, змінюючи значення прикладених сил та їх плечі.
6. Зробіть висновок щодо виконання умов рівноваги важеля.
7. Причепіть до одного плеча важеля 2-3 тягарці. Замість тягарців для створення моменту врівноважуючої сили використайте динамометр. Змінюючи напрямок сили, з якою діє на інше плече важеля динамометр, з’ясуйте, за яких умов ця сила буде найменшою.
8. Зробіть відповідні висновки.