Головна ⇒ 📌Математика ⇒ Відсотки. Знаходження відсотків від даного числа

Відсотки. Знаходження відсотків від даного числа

Розділ 2 ДРОБОВІ ЧИСЛА І Дії З НИМИ

§ 42. Відсотки. Знаходження відсотків від даного числа

Під час різних обчислень людям часто доводиться знаходити частини числа: 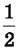Відсотки. Знаходження відсотків від даного числа (половину), 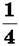Відсотки. Знаходження відсотків від даного числа (четвертину), 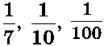Відсотки. Знаходження відсотків від даного числа і т. д.

Найзручніше в таких обчисленнях знаходити соті частини числа, або відсотки (проценти)1, оскільки при цьому доводиться множити чи ділити на число 100.

Відсотком (процентом) називається сота частина 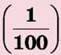Відсотки. Знаходження відсотків від даного числа будь-якого числа (або числового значення

величини).

Для позначення відсотка (процента) використову ють знак %:

Відсотки. Знаходження відсотків від даного числа

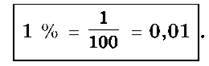
1 Слово “процент” походить від латинського слова per cent – на сотню, що вказує на зменшення одиниці виміру в сто разів. Наприклад, сантиметр – сота частина метра 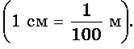Відсотки. Знаходження відсотків від даного числа

Знайти 1 % від числа – значить, знайти одну соту частину цього числа.

Задача 1. Знайди 1 % від 400 грн.

Розв’язання. Приймаємо 400 грн. за 100 %. Щоб знайти 1 %, потрібно 400 грн. поділити на 100. 400 : 100 = 4 грн.

Соту частину центнера називають кілограмом, соту частину метра – сантиметром, соту частину гектара – аром (або

соткою). Наприклад, кілограм – це один відсоток центнера, сантиметр – один відсоток метра, ар – один відсоток гектара.

Можна записати також:

Відсотки. Знаходження відсотків від даного числа

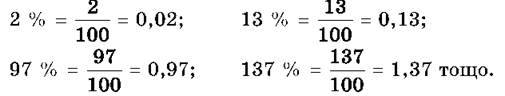
Щоб перетворити відсотки в десятковий дріб, треба поділити число процентів на 100. Оскільки 1 % дорівнює сотій частині величини, то

Вся величина дорівнює 100 %. Отже, 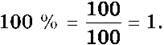Відсотки. Знаходження відсотків від даного числа

Щоб перетворити десятковий дріб у відсотки, треба його помножити на 100.

Наприклад: 0,8 = 0,8 ∙ 100 % = 80 %; 0,42 = = 0,42 ∙ 100 % = 42 %; 0,372 = 0,372 ∙ 100 % = 37,2 %.

Щоб перетворити звичайний дріб у відсотки, треба спочатку перетворити його в десятковий, а потім помножити отриманий десятковий дріб на 100.

Наприклад: 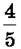Відсотки. Знаходження відсотків від даного числа = 4 : 5 = 0,8; 0,8 ∙ 100 % = 80 %;

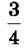Відсотки. Знаходження відсотків від даного числа = 3 : 4 = 0,75; 0,75 ∙ 100 % = 75 %.

Деякі з рівностей між звичайними дробами і відсотками доцільно запам’ятати!

Відсотки. Знаходження відсотків від даного числа

Розглянемо задачу знаходження відсотків від заданого числа.

Задача 2. Молоко містить 4 % жиру. Скільки жиру міститься в 800 кг молока?

Розв’язання. 1-й спосіб. Знайдемо спочатку 1 % від числа 800. Для цього треба 800 поділити на 100. Маємо 800 : 100 = 8. Отриманий результат треба помножити на кількість відсотків. Маємо 8 ∙ 4 = 32 кг. Отже, у 800 кг молока міститься 32 кг жиру.

2-й спосіб. Цей самий результат можна було отримати по-іншому: 4 % = 0,04. Якщо виконати множення 800 на 0,04, то отримаємо 800 ∙ 0,04 = 32 кг. Отже, розв’язуючи першим способом, ми знайшли, скільки кілограмів жиру припадає на 1 %, потім помножили цю кількість на відповідний відсоток, а розв’язуючи другим способом, виразили відсоток десятковим дробом і помножили дане число на цей дріб.

Початковий рівень

1494. Запиши у вигляді десяткового дробу:

1) 7 %; 2) 13 %; 3) 97 %;

4) 132 %; 5) 145 %; 6) 217 %.

1495. Запиши у вигляді десяткового дробу:

1) 19 %; 2) 49 %; 3) 197 %; 4) 359 %.

1496. Запиши у відсотках десяткові дроби:

1) 0,42; 2) 0,03; 3) 0,5;

4) 1,18; 5) 0,318; 6) 2,387.

1497. Запиши у відсотках десяткові дроби:

1) 0,39; 2) 0,07; 3) 0,2;

4) 1,17; 5) 1,189; 6) 7,32.

Середній рівень

1498. Запиши звичайні дроби у вигляді десяткових, а потім у вигляді відсотків:

Відсотки. Знаходження відсотків від даного числа

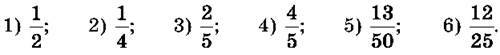
1499. Запиши звичайні дроби у вигляді десяткових, а потім у вигляді відсотків:

Відсотки. Знаходження відсотків від даного числа

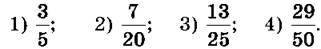
1500. Заповни таблицю.

Звичайний дріб

3

4

1

20

1

25

Десятковий дріб

0,25

0,02

Відсоток

20 %

100 %

1501. (Усно). З молока виходить 9 % сиру. Скільки сиру можна отримати зі 100 кг молока?

1502. У шкільній бібліотеці 800 книжок. Сергій прочитав за рік одну соту частину всіх цих книжок, а Іван – 1 % усіх книжок шкільної бібліотеки. Порівняй кількість книжок, які прочитали Сергій та Іван.

1503. Бригаді доручили відремонтувати ділянку дороги завдовжки 900 м. Скільки метрів дороги бригада відремонтує, якщо виконає 5 % завдання? 27 % завдання? 60 % завдання?

1504. Скільки відсотків від 1 м становлять:

1) 1 см; 2) 5 см; 3) 1 дм;

4) 3 дм; 5) 0,32 м; 6) 1 м?

1505. Скільки відсотків від 1 ц становлять:

1) 1 кг; 2) 7 кг; 3) 13 кг;

4) 0,5 ц; 5) 1 ц; 6) 1,2 ц?

1506. Із цукрової тростини отримують 18 % цукру. Скільки кілограмів цукру отримають із 7000 кг тростини?

1507. Площа поля становить 400 га. Пшеницею засіяли 25 % поля, а картоплею – 7 %. Скільки гектарів поля засіяли пшеницею і скільки картоплею?

1508. 5-А і 5-Б класи виготовили 200 ялинкових прикрас. Із них 65 % виготовив 5-А клас. Скільки прикрас виготовив 5-Б клас?

1509. Петро та Орест разом мають 200 марок. З них 42 % марок має Петро. Скільки марок в Ореста?

1510. Скільки відсотків площі великого прямокутника (рис. 260):

1) зафарбовано;

2) позначено плюсами;

3) позначено мінусами;

4) позначено кружечками?

Відсотки. Знаходження відсотків від даного числа

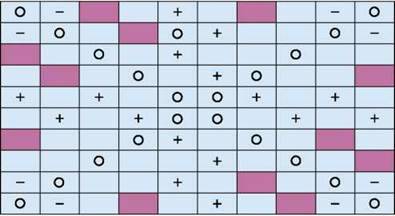
Рис. 260

1511. Накресли квадрат зі стороною 10 см і поділи його на 100 рівних квадратиків. Заштрихуй на рисунку:

1) 1 % цих квадратиків у синій колір;

2) 5 % цих квадратиків у зелений колір;

3) 12 % цих квадратиків у червоний колір.

1512. Знайди:

1) 10 % від 120; 320;

2) 20 % від 1 м 20 см; 5 ц 30 кг;

3) 35 % від 1020; 780;

4) 65 % від 4 грн.; 5 кг.

1513. Знайди:

1) 5 % від 80; 195;

2) 30 % від 214 м; 5 кг;

3) 45 % від 5 грн. 20 коп.; 10 т;

4) 90 % від 113; 320.

1514. Полуниці містять у середньому 6 % цукру. Скільки кілограмів цукру міститься у 15 кг полуниць?

1515. Сплав містить 17 % цинку. Скільки кілограмів цинку міститься в 180 кг сплаву?

1516. Огірки містять у середньому 95 % води. Скільки кілограмів води в 42 кг огірків?

1517. Тіло людини містить приблизно 64 % води. Скільки кілограмів води у тілі людини, якщо її маса 45 кг?

1518. Довжина прямокутника 75 см, а ширина становить 80 % довжини. Знайди площу прямокутника.

1519. Три п’ятих класи зібрали разом 3600 кг макулатури. Перший клас зібрав 32 % усієї макулатури, другий – 30 %. Скільки кілограмів макулатури зібрав третій клас?

1520. Машина мала подолати відстань 240 км за 3 год. За першу годину вона проїхала 35 % цієї відстані, а за другу – 38 % цієї відстані. Скільки кілометрів проїхала машина за третю годину?

1521. У класі 30 учнів, 40 % з яких – хлопці. Кого в класі більше: хлопців чи дівчат? На скільки?

1522. Поїзд проїхав 160 км. За першу годину він подолав 48 % цієї відстані, а потім зупинився. Коли потяг проїхав більшу відстань: до зупинки чи після? На скільки?

1523. Дано квадрат зі стороною 5 см. Знайди 36 % площі цього квадрата.

Достатній рівень

1524. Під час сушіння яблука втрачають 91 % своєї маси. Скільки сухих яблук одержимо з 250 кг свіжих?

1525. Під час сушіння картопля втрачає 85 % своєї маси. Скільки сухої картоплі отримаємо зі 120 кг свіжої?

1526. Площа всієї поверхні Землі становить 510 100 тис. км2, суходіл займає 29 % цієї площі, а решту вкрито водою. Яка площа поверхні Землі вкрита водою?

1527. За планом токар мав виготовити 80 деталей за день, але він перевиконав план на 5 %. Скільки деталей виготовив токар?

1528. Фермер розраховував збирати по 290 ц з 1 га. Проте урожай виявився більшим на 10 %. Який урожай зібрав фермер з ділянки 8 га?

1529. Собівартість деякої деталі становила 480 грн. Унаслідок упровадження нової технології її собівартість вдалося знизити на 5 %. Якою стала собівартість деталі?

1530. У садку ростуть 150 дерев, з них 40 % яблуні, а вишні становлять 75 % від кількості яблунь. Скільки вишень росте в садку?

1531. Із 750 учнів школи 60 % відвідують різні гуртки, з них 4 % – шаховий. Скільки учнів відвідують шаховий гурток?

1532. Турист планував подолати 80 км за три дні. За перший день він подолав 35 % запланованої відстані, а за другий – 55 % решти. Скільки кілометрів треба подолати туристу за третій день?

1533. З 5000 осіб дорослого населення селища 40 % працюють в районному центрі, а 20 % решти – на підприємствах селища. Скільки осіб працює на підприємствах селища?

1534. Банк виплачує 18 % річних. Вкладник поклав до банку 5000 грн. Скільки грошей буде в нього на рахунку через рік? Через два роки?

1535. Бак має форму прямокутного паралелепіпеда, виміри якого 15 дм, 20 дм і 10 дм. Водою заповнено 80 % його об’єму. Скільки літрів води в баці?

1536. Промінь, проведений з вершини розгорнутого кута, ділить його на два кути. Один з кутів становить 55 % розгорнутого кута. Обчисли градусні міри обох кутів.

1537. Довжина ділянки прямокутної форми 450 м, а ширина становить 80 % довжини. З кожного гектара ділянки зібрали по 40 ц пшениці. Скільки центнерів пшениці зібрали з усієї ділянки?

Високий рівень

1538. Число збільшили на 100 %. У скільки разів збільшилося число?

Вправи для повторення

1539. 1) Яке число треба додати до 5,18, щоб отримати 10?

2) До якого числа треба додати 32,47, щоб отримати 59,16?

1540. Обчисли периметр прямокутника, якщо його ширина 4,2 дм, а довжина на 1,5 дм більша.

1541. У перший магазин завезли 325 кг овочів, у другий – 487 кг, а в третій – 392 кг. Скільки кілограмів овочів завезли в три магазини разом? Результат округли до десятків. Порівняй відповідь з результатом, який дістанемо, якщо спочатку округлити дані задачі до десятків, а потім її розв’язати.


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (2 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Відсотки. Знаходження відсотків від числа Урок 117 Тема. Відсотки. Знаходження відсотків від числа Мета: сформувати вміння, відпрацювати навички знаходження відсотків від числа; провести діагностику засвоєння знань і вмінь. Тип уроку: застосування знань, навичок і вмінь. Хід уроку I. Розминка Усні вправи 1. Розчин містить сіль і воду. Сіль становить 9% розчину. Скільки відсотків становить вода? 2. Сплав складається з міді, […]...

  2. Відсотки. Знаходження відсотків від числа Розділ II ДРОБОВІ ЧИСЛА І ДІЇ З НИМИ § 5. ДЕСЯТКОВІ ДРОБИ 37. Відсотки. Знаходження відсотків від числа На практиці люди часто користуються сотими частинами величин. Наприклад, сота частина гектара – 1 ар (1 сотка), сота частина століття – 1 рік, сота частина гривні – 1 копійка, сота частина метра – 1 сантиметр. Для сотої […]...

  3. Знаходження відсотків від числа Урок № 57. Тема. Знаходження відсотків від числа Мета уроку. Ознайомити учнів з задачами на знаходження відсотків від числа; сформулювати правило знаходження відсотків від числа, вчити учнів використовувати його при розв’язувані задач. Хід уроку І. Перевірка домашнього завдання Два учні на дошці відтворюють розв’язання домашніх вправ №№ 7,9. тестові завдання стор. 312. ІІ. Повторення вивченого […]...

  4. Відсотки Математика – Алгебра Відсотки Відсотком називають (0,01) і по­значають 1%. Один відсоток від якої-небудь величини означає 0,01 цієї величини. Наприклад, 1% від 500 м дорівнює 5 м; 4% від 320 т дорівнюють (т). 100% деякої величини – це сама вели­чина. Будь-який десятковий дріб можна записати у відсотках. Для цього його треба помножити на 100: ; […]...

  5. Знаходження дробу від числа Розділ 2 Звичайні дроби §15. Знаходження дробу від числа Розглянемо задачу, що зводиться до знаходження дробу від числа. Задача 1. У класі 30 учнів, із них хлопці. Скільки хлопців у класі? Розв’язання. (Мал. 3). 1) 30 : 5 = 6 (уч.) – становить від 30 учнів; 2) 6 ∙ 2 = 12 (уч.) – становить […]...

  6. Знаходження дробу від числа ст.99 Знаходження дробу від числа 1 Знайди дріб від числа. від 72; від 88; від 48. 2 Зістав задачі 1 і 2. Що в них спільне? відмінне? Розв’яжи задачу 1. Розв’яжи задачу 2. Запиши розв’язання задачі 2 по діях і виразом. Прочитай одержаний вираз і поясни, що позначає кожне числе Спробуй сформулювати, використавши слова “чи сельник” […]...

  7. Властивості пропорції – ПРОПОРЦІЇ. ВІДСОТКИ Формули й таблиці МАТЕМАТИКА ПРОПОРЦІЇ. ВІДСОТКИ Відношення числа а до числа b – дріб a/b. Пропорція – рівність двох відношень: a/b = c/d. Основна властивість пропорції Якщо a/b = c/d правильно, то ad = bc. Властивості пропорції А) a/b = c/d правильна → a/c = b/d правильна; Б) a/b = c/d правильна → d/b = […]...

  8. Відсотки. Розв’язування вправ на вираження відсотків числами та навпаки Урок № 56. Тема. Відсотки. Розв’язування вправ на вираження відсотків числами та навпаки Мета уроку. Вироблення навиків по використанню правил по запису відсотків числами та навпаки. Хід уроку I. Перевірка домашнього завдання За готовими розв’язками, записаними на дошці: №№ 1625, 1629. Фронтально: № 1634 (а). II. Актуалізація опорних знань Робота в групах. Учні класу діляться […]...

  9. Читання і записування чотирицифрових чисел. Знаходження частини числа і числа за його частиною. Задачі, які включають знаходження частини числа (№№ 185-193) Тема. Читання і записування чотирицифрових чисел. Знаходження частини числа і числа за його частиною. Задачі, які включають знаходження частини числа (№№ 185-193). Мета. Ознайомити учнів з правилом записування будь-якого чотирицифрового числа; закріплювати вміння учнів читати чотирицифрові числа; повторити правило знаходження частини числа і числа за його частиною, розв’язувати задачі двома способами. Обладнання. Нумераційна таблиця; таблиця […]...

  10. Відсотки. Записування відсотків десятковим дробом або натуральним числом Урок № 54. Тема. Відсотки. Записування відсотків десятковим дробом або натуральним числом Мета уроку. Ознайомити з означенням відсотка, уміти записувати відсотки числом. Обладнання. Таблиця “Відсотки”. Хід уроку I. Перевірка домашнього завдання Учитель з’ясовує стан виконання домашньої роботи. Якщо у когось виникли запитання, то за допомогою учнів і самого учителя дають на них відповіді. II. Тестові […]...

  11. Складені задачі, які містять знаходження дробу від числа Складені задачі, які містять знаходження дробу від числа 1 Знайди: 1) від 98; від 95; від 51; від 64. 2) число, якщо його становлять 98; Число, якщо його становлять 95. 2 Знайди, скільки: Метрів у км, у км; кілограмів у ц, у т. 3 Знайди, записавши відповідні вирази. 1) числа b; числа 125; числа k; […]...

  12. Знаходження числа за величиною його дробу Знаходження числа за величиною його дробу 1 Покажи ціле, знаючи його частину. 1) – це цілого. 2) – це цілого. 3 Віднови цілу смужку, якщо її мають такий вигляд: Софійка вважає, що для відновлення смужки треба спочатку знайти величину однієї сьомої частини смужки. Для цього треба виміряти довжину смужки і розділити її на 5. Оскільки […]...

  13. ЗНАХОДЖЕННЯ ДРОБУ ВІД ЧИСЛА ТА ЧИСЛА ЗА ЙОГО ДРОБОМ РОЗДІЛ 5 ЗВИЧАЙНІ ДРОБИ § 25. ЗНАХОДЖЕННЯ ДРОБУ ВІД ЧИСЛА ТА ЧИСЛА ЗА ЙОГО ДРОБОМ У попередніх параграфах ви дізналися, що таке дріб, з’ясували, що показує чисельник дробу, а що – його знаменник. На практиці доводиться знаходити число, яке від даного числа становить, наприклад, тощо. Такі задачі називають задачами на знаходження дробу від числа. їх […]...

  14. ЩО ТАКЕ ВІДСОТОК. ЗНАХОДЖЕННЯ ВІДСОТКА ВІД ЧИСЛА РОЗДІЛ 8 ВІДСОТКИ. СЕРЕДНЄ АРИФМЕТИЧНЕ У розділі дізнаєтесь: Що таке відсоток та як його позначають; Як подати відсоток десятковим та звичайним дробом; Як знаходити відсоток від числа; Як знаходити число за його відсотком; Як знаходити середнє арифметичне чисел та середнє значення величин; Як застосувати вивчений матеріал на практиці § 34. ЩО ТАКЕ ВІДСОТОК. ЗНАХОДЖЕННЯ ВІДСОТКА […]...

  15. Знаходження числа за його дробом Розділ 2 Звичайні дроби §18. Знаходження числа за його дробом Розглянемо задачу, що зводиться до знаходження числа за його дробом. Задача 1. Сергій прочитав 120 сторінок. Це становить книжки. Скільки сторінок у книжці? Розв’язання. Умову задачі зображено на малюнку 4. 1) 120 : 3 = 40 (с.) – припадає на Книжки; 2) 40 ∙ 5 […]...

  16. Знаходження числа за його відсотком Розділ 2 ДРОБОВІ ЧИСЛА І Дії З НИМИ § 43. Знаходження числа за його відсотком Ми вже вміємо знаходити відсоток від числа. Розглянемо задачу знаходження числа за його відсотком. Задача. Учень прочитав 120 сторінок, що становить 30 % числа всіх сторінок у книжці. Скільки сторінок у книжці? Розв’язання. 1-й спосіб. Знайдемо кількість сторінок, яка припадає […]...

  17. Задачі на ділення дробів. Знаходження числа за його дробом Урок № 3 3 Тема. Задачі на ділення дробів. Знаходження числа за його дробом Мета: домогтися засвоєння учнями алгоритму розв’язування задач на знаходження числа за його дробом (відсотками); повторити алгоритми розв’язування інших задач на ділення; виробляти вміння розв’язувати задачі на застосування названих алгоритмів. Тип уроку: засвоєння знань та вмінь. Хід уроку І. Актуалізація опорних знань […]...

  18. Множення іменованих чисел на двоцифрові числа. Порівняння задач на знаходження числа за двома різницями. Запис периметра і площі квадрата у загальному вигляді. Розв’язування задач на знаходження числа за його дробом (№№ 942-949) Тема. Множення іменованих чисел на двоцифрові числа. Порівняння задач на знаходження числа за двома різницями. Запис периметра і площі квадрата у загальному вигляді. Розв’язування задач на знаходження числа за його дробом (№№ 942-949). Мета. Ознайомити учнів із множенням складених іменованих чисел на двоцифрові числа; удосконалювати вміння розв’язувати задачі на знаходження числа за двома різницями, порівнювати […]...

  19. Множення і ділення на 10 і на 100. Задачі, які включають знаходження частини числа або числа за його частиною (№№ 82-91) Тема. Множення і ділення на 10 і на 100. Задачі, які включають знаходження частини числа або числа за його частиною (№№ 82 – 91). Мета. Закріпити навички множення і ділення круглих чисел на 10 і на 100; вправляти учнів у розв’язуванні задач, які включають знаходження частини числа або числа за його частиною. Обладнання. Таблиця усних […]...

  20. ЗНАХОДЖЕННЯ ЧАСТИНИ ЧИСЛА. ПИСЬМОВЕ ДІЛЕННЯ НА ОДНОЦИФРОВЕ ЧИСЛО. ЗАДАЧІ НА ЗНАХОДЖЕННЯ ЧИСЛА ЗА ЗНАЧЕННЯМ ЙОГО ДРОБУ Мета: повторити правило знаходження частини числа; закріпити вміння розв’язувати задачі на знаходження частини числа за значенням його дробу; вчити виконувати письмове ділення; розвивати мислення; виховувати інтерес до предмета. ХІД УРОКУ I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. КОНТРОЛЬ, КОРЕКЦІЯ І ЗАКРІПЛЕННЯ ЗНАНЬ 1. Перевірка домашнього завдання 2. Усні обчислення. Гра “День – ніч” 3. Математичний диктант – Запиши […]...

  21. Вправи на знаходження частини числа. Письмове ділення на одноцифрове число. Задачі, які включають знаходження частини числа (№№ 62-70) Тема. Вправи на знаходження частини числа. Письмове ділення на одноцифрове число. Задачі, які включають знаходження частини числа (№№ 62 – 70). Мета. Формувати вміння розв’язувати задачі, які включають знаходження частини числа; закріплювати навички ділення трицифрового числа на одноцифрове. Обладнання. Таблиця усних обчислень (гра “Комп’ютер”); картки для опитування; схеми задач. Зміст уроку І. Контроль, корекція і […]...

  22. Складені задачі, які містять знаходження дробу від числа ст. 108 Складені задачі, які містять знаходження дробу від числа 1 Розташуй числа в порядку зростання. ; ; ; ; 1; ; ; ; ; ; ; ; 2 Знайди: 1) від 92; від 168; від 81; від 90; 2) число, якщо його становлять 92; число, якщо його становлять 1 бо; число, якщо його становлять 81; число, […]...

  23. Відсотки. Вираження числа відсотками Урок № 55. Тема. Відсотки. Вираження числа відсотками Мета уроку. Уміти виражати зміну величини різними способами. Обладнання. Картки для індивідуальної роботи з учнями, таблиця “Відсотки”. Хід уроку I. Актуалізація опорних знань 1. Що означає знак %? Дати означення відсотка. 2. Знайти 1 % чисел: 6000; 200; 450; 70; 20. 3. В класі присутні 92 % […]...

  24. Відсоткові розрахунки. Формула складних відсотків УРОК № 42 Тема. Відсоткові розрахунки. Формула складних відсотків Мета уроку: закріпити знання учнів про формули розв’язування основних задач на відсотки. Продовжити роботу над виробленням умінь застосовувати вивчені формули для розв’язування задач на відсоткові розрахунки. Повторити розв’язання задач на складання та розв’язування математичних моделей. Тип уроку: закріплення знань, відпрацювання вмінь. Наочність та обладнання: опорний конспект […]...

  25. Знаходження числа за його частиною. Письмове ділення на одноцифрове число. Задачі на знаходження числа за його частиною (№№ 71-81) Тема. Знаходження числа за його частиною. Письмове ділення на одноцифрове число. Задачі на знаходження числа за його частиною (№№ 71 – 81). Мета. Формувати вміння розв’язувати задачі, які включають знаходження числа за його частиною; закріплювати навички ділення на одноцифрове число. Обладнання. Таблиця усних обчислень; “Картки для поточного контролю знань”; сигнальні картки. Зміст уроку І. Контроль, […]...

  26. Усне множення двоцифрових і круглих багатоцифрових чисел на розрядні числа. Складені задачі, розв’язання яких вимагає знаходження дробу від числа (№№ 814-822) Тема. Усне множення двоцифрових і круглих багатоцифрових чисел на розрядні числа. Складені задачі, розв’язання яких вимагає знаходження дробу від числа (№№ 814-822). Мета. Закріплювати вміння учнів виконувати усне множення двоцифрових і круглих багатоцифрових чисел на розрядні числа; удосконалювати вміння розв’язувати складені задачі, розв’язання яких вимагає знаходження дробу від числа. Обладнання. Таблиця “Множення багатоцифрових чисел на […]...

  27. ДІЛЕННЯ ДРОБІВ. ЗНАХОДЖЕННЯ ЧИСЛА ЗА ЙОГО ДРОБОМ Розділ 2 ЗВИЧАЙНІ ДРОБИ ТА ДІЇ З НИМИ § 10. ДІЛЕННЯ ДРОБІВ. ЗНАХОДЖЕННЯ ЧИСЛА ЗА ЙОГО ДРОБОМ Ви знаете, що невідомий множник знаходять діленням добутку на відомий множник. Наприклад, у прямокутника з площею дм2 й однією зі сторін дм (мал. 9) друга сторона дорівнює частці від ділення дробу Мал. 9 Нехай шуканою часткою є дріб […]...

  28. ЗНАХОДЖЕННЯ ЧИСЛА ЗА ЙОГО ДРОБОМ Цілі: – навчальна: удосконалити вміння виконувати вправи, у яких передбачено знаходження числа за його дробом; узагальнити та систематизувати знання учнів з теми “Звичайні дроби”; – розвивальна: формувати вміння аналізувати інформацію, узагальнювати та робити висновки; – виховна: виховувати відповідальність за результати своєї роботи, свідоме ставлення до навчання; Тип уроку: комбінований. Обладнання та наочність: Хід уроку І. […]...

  29. ЗНАХОДЖЕННЯ ДРОБУ ВІД ЧИСЛА Цілі: – навчальна: удосконалити вміння виконувати вправи, у яких передбачено знаходження дробу від числа; – розвивальна: формувати вміння бачити закономірності, міркувати за аналогією; – виховна: виховувати наполегливість у досягненні мети, творче ставлення до справи; Тип уроку: удосконалення вмінь і навичок. Обладнання та наочність: Хід уроку І. ОРГАНІЗАЦІЙНИЙ ЕТАП ____________________________________________ ____________________________________________ ____________________________________________ II. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ […]...

  30. ЧИТАННЯ І ЗАПИСУВАННЯ ЧОТИРИЦИФРОВИХ ЧИСЕЛ. ЗНАХОДЖЕННЯ ЧАСТИНИ ЧИСЛА ТА ЧИСЛА ЗА ЗНАЧЕННЯМ ЙОГО ЧАСТИНИ ОРІЄНТОВНА НАВЧАЛЬНА МЕТА: ФОРМУВАТИ ВМІННЯ ЧИТАТИ Й ЗАПИСУВАТИ ЧОТИРИЦИФРОВІ ЧИСЛА; ПОВТОРИТИ ЗНАХОДЖЕННЯ ЧАСТИНИ ЧИСЛА ТА ЧИСЛА ЗА ЙОГО ЧАСТИНОЮ I. Перевірка домашнього завдання На дошці записано вирази: 60 : 12 60 : 12 + 24 : 12 (60 + 24) : 12 Який з них є розв’язком задачі 184? Взаємоперевірка вправи 183. II. Актуалізація та […]...

  31. Знаходження числа за його відсотками Урок 121 Тема. Знаходження числа за його відсотками Мета: узагальнити й систематизувати знання учнів про види задач, що розв’язуються із застосуванням алгоритму знаходження числа за його відсотками; здійснити діагностику засвоєння знань і сформованих умінь учнів. Тип уроку: узагальнення і систематизація знань. Хід уроку I. Розминка Усні вправи 1. Знайдіть числа, яких не вистачає в ланцюжку […]...

  32. Знаходження значень виразів на сумісні дії. Задачі на знаходження числа за двома різницями (№№ 950-958) Тема. Знаходження значень виразів на сумісні дії. Задачі на знаходження числа за двома різницями (№№ 950 – 958). Мета. Закріплювати вміння учнів знаходити значення виразів на сумісні дії; удосконалювати вміння розв’язувати задачі на знаходження числа за двома різницями. Обладнання. Таблиця “Знаходження значень виразів на сумісні дії”; сигнальні картки; таблиця для короткого запису задачі. Зміст уроку […]...

  33. Множення трицифрових чисел на двоцифрові. Задачі на знаходження числа за двома різницями. Задачі на знаходження дробу від числа і числа за ного дробом (№№ 928-934) Тема. Множення трицифрових чисел на двоцифрові. Задачі на знаходження числа за двома різницями. Задачі на знаходження дробу від числа і числа за ного дробом (№№ 928-934). Мета. Ознайомити учнів із множенням трицифрових чисел на двоцифрові; закріплювати вміння учнів розв’язувати задачі на знаходження числа за двома різницями; удосконалювати вміння учнів розв’язувати задачі на знаходження дробу від […]...

  34. МНОЖЕННЯ ДРОБІВ. ЗНАХОДЖЕННЯ ДРОБУ ВІД ЧИСЛА Розділ 2 ЗВИЧАЙНІ ДРОБИ ТА ДІЇ З НИМИ § 9. МНОЖЕННЯ ДРОБІВ. ЗНАХОДЖЕННЯ ДРОБУ ВІД ЧИСЛА Дроби, як і натуральні числа, можна множити. Наприклад, щоб знайти площу прямокутника зі сторонами 3 см і 4 см, треба помножити ці числа: 3 ∙ 4 = 12 (см2). Але Тому, у квадратних дециметрах площа даного прямокутника дорівнює добутку […]...

  35. Аналіз контрольної роботи. Частини. Порівняння частин. Задачі на знаходження частини числа і числа за його частиною. Складені задачі, які включають знаходження частин (№№ 751-759) Тема. Аналіз контрольної роботи. Частини. Порівняння частин. Задачі на знаходження частини числа і числа за його частиною. Складені задачі, які включають знаходження частин (№№ 751-759). Мета. Проаналізувати помилки, допущені учнями під час виконання контрольної роботи; вчити учнів знаходити частину числа та число за його частиною; удосконалювати вміння учнів розв’язувати складені задачі, які включають знаходження частин. […]...

  36. МНОЖЕННЯ Й ДІЛЕННЯ НА РОЗРЯДНІ ОДИНИЦІ 10; 100. ЗАДАЧІ НА ЗНАХОДЖЕННЯ ЧИСЛА ЗА ЙОГО ЧАСТИНОЮ І ЧАСТИНИ ВІД ЧИСЛА Мета: вдосконалювати вміння розв’язувати задачі на знаходження числа за його частиною і частини від числа; закріплювати навички ділення і множення на одноцифрове число, на розрядну одиницю 10; 100; розвивати мислення; виховувати уважність. ХІД УРОКУ I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. КОНТРОЛЬ, КОРЕКЦІЯ І ЗАКРІПЛЕННЯ ЗНАНЬ 1. Перевірка домашнього завдання Завдання 80 – Прочитайте відповідь, поясніть вибір дії. […]...

  37. Тематичне оцінювання № 9 по темі “Відсотки” Урок № 62 Тема. Тематичне оцінювання № 9 по темі “Відсотки” Мета уроку. Діагностика та контроль якості засвоєння відсотків. Хід уроку I. Організаційна частина На розсуд вчителя. II. Запис та виконання вправ і задач учнями ВАРІАНТ 1. 1).° Запишіть у вигляді звичайного і десяткового дробів: 9%, 31%, 105%, 180%. 2).° Записати у відсотках: 7/100, 3/10, […]...

  38. Знаходження числа за його частиною. Перевірка письмового ділення множенням УРОК 7 Тема. Знаходження числа за його частиною. Перевірка письмового ділення множенням Мета: розвивати вміння учнів виконувати письмове ділення та розв’язувати задачі, пов’язані з поняттям частина числа; розвивати логічне мислення, увагу. Обладнання: картки з тестами, картки для усної лічби, креслення. ХІД УРОКУ I. Контроль і закріплення знань учнів Тест для перевірки знань, отриманих раніше (Кожне […]...

  39. ЗНАХОДЖЕННЯ ЧИСЛА ЗА ЙОГО ЧАСТИНОЮ. ПИСЬМОВЕ ДІЛЕННЯ НА ОДНОЦИФРОВЕ ЧИСЛО. ЗАДАЧІ НА ЗНАХОДЖЕННЯ ЧИСЛА ЗА ЙОГО ЧАСТИНОЮ Мета: повторити і закріпити правило знаходження числа за його частиною; вчити розв’язувати задачі на знаходження числа за його частиною, виконувати ділення на одноцифрове число; розвивати мислення; виховувати інтерес до предмета. ХІД УРОКУ I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ III. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. Усні обчислення Гра “Ланцюжок” 40 збільш на 60; зменш на 2; […]...

  40. ЧИТАННЯ І ЗАПИС ЧОТИРИЦИФРОВИХ ЧИСЕЛ. ЗАДАЧІ НА ЗНАХОДЖЕННЯ ЧИСЛА ЗА ЙОГО ЧАСТИНАМИ І ЧАСТИНИ ВІД ЧИСЛА Мета: ознайомити учнів з правилом запису будь-якого чотирицифрового числа; закріплювати вміння читати чотирицифрові числа; повторити правило знаходження частини числа і числа за його частиною; вдосконалювати навички усних і письмових обчислень, розв’язування задач двома способами; розвивати мислення; виховувати інтерес до предмета. ХІД УРОКУ I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ Завдання 183 – Прочитайте числа, в […]...

Ви зараз читаєте: Відсотки. Знаходження відсотків від даного числа
«
»