ВИРАЗИ ТА ЇХ СПРОЩЕННЯ
Розділ 5 ВИРАЗИ І РІВНЯННЯ
У розділі дізнаєтесь:
Ü про вирази та їх спрощення;
Ü які є властивості рівностей;
Ü як розв’язувати рівняння на основі властивостей рівностей;
Ü які види задач розв’язують за допомогою рівнянь; що таке перпендикулярні прямі та як їх будувати;
Ü які прямі називаються паралельними та як їх будувати;
Ü що таке координатна площина;
Ü як визначити координати точки на площині;
Ü що таке графік залежності між величинами та як його побудувати;
Ü як застосувати вивчений матеріал на

§ 30. ВИРАЗИ ТА ЇХ СПРОЩЕННЯ
Ви вже знаєте, що таке буквені вирази, і вмієте їх спрощувати за допомогою законів додавання і множення. Наприклад, 2а ∙ (-4b) = -8ab. В отриманому виразі число -8 називають коефіцієнтом виразу.
? Чи має вираз cd коефіцієнт? Так. Він дорівнює 1, оскільки cd – 1 ∙ cd.
Пригадаємо, що перетворення виразу з дужками у вираз без дужок називають розкриттям, дужок. Наприклад: 5(2х + 4) = 10х+ 20.
Обернена дія в цьому прикладі – це винесення спільного множника за дужки.
Доданки, які містять однакові буквені множники, називають подібними доданками. За допомогою
5х + y + 4 – 2х + 6y – 9 =
= (5х – 2х) + (y + 6y)+ (4 – 9) = = (5-2)* + (1 + 6)*y-5 =
= bх+ 7у – 5.
Правила розкриття дужок
1. Якщо перед дужками стоїть знак”+”, то під час розкриття дужок знаки доданків у дужках зберігають;
2. Якщо перед дужками стоїть знак “-“, то під час розкриття дужок знаки доданків у дужках змінюють на протилежні.
Задача 1 . Спростіть вираз:
1) 4х+(-7х + 5);
2) 15y-(-8 + 7y).
Розв’язання. 1. Перед дужками стоїть знак “+”, тому : під час розкриття дужок знаки всіх доданків зберігаються:
4х +(-7х + 5) = 4х – 7х + 5=-3х + 5.
2. Перед дужками стоїть знак”-“, тому під час розкриття дужок : знаки всіх доданків змінюються на протилежні:
-15у – (- 8 + 7у) = 15у + 8 – 7у = 8у +8.
Для розкриття дужок використовують розподільну властивість множення: а(b + c) = ab + ас. Якщо а > 0, то знаки доданків b і с не змінюють. Якщо а < 0, то знаки доданків b і с змінюють на протилежні.
Задача 2. Спростіть вираз:
1) 2(6y-8) + 7y;
2)-5(2-5х) + 12.
Розв’язання. 1. Множник 2 перед дужками е додатним, тому під час розкриття дужок знаки всіх доданків зберігаємо: 2(6y – 8) + 7y= 12y – 16 + 7y=19y-16.
2. Множник -5 перед дужками е від’ємним, тому під час розкриття дужок знаки всіх доданків змінюємо на протилежні:
-5(2 – 5х) + 12 = -10 + 25х +12 = 2 + 25х.
Дізнайтеся більше
1. Слово “сума” походить від латинського summa, що означає “підсумок”, “загальна кількість”.
2. Слово “плюс” походить від латинського plus, що означає “більше”, а слово “мінус” – від латинського minus, що означає “менше”. Знаки “+” і”-” використовують для позначення дій додавання і віднімання. Ці знаки ввів чеський учений Й. Відман у 1489 р. в книзі “Швидкий і приємний рахунок для всіх торговців” (мал. 138).

Мал. 138
ПРИГАДАЙТЕ ГОЛОВНЕ
1. Які доданки називають подібними? Як зводять подібні доданки?
2. Як розкривають дужки, перед якими стоїть знак “+”?
3. Як розкривають дужки, перед якими стоїть знак “-“?
4. Як розкривають дужки, перед якими стоїть додатний множник?
5. Як розкривають дужки, перед якими стоїть від’ємний множник?
1374′. Назвіть коефіцієнт виразу:
1)12 а; 3)-5,6 ху;
2)4 6; 4 )-с.
1375′. Назвіть доданки, які відрізняються лише коефіцієнтом:
1) 10а + 76-26 + а; 3) 5n + 5m-4n + 4;
2) bc-4d-bc + 4d; 4)5х + 4у-х + у.
Як називають такі доданки?
1376′. Чи є подібними доданки у виразі:
1)11а+10а; 3)6n + 15n; 5) 25р – 10р + 15р;
2) 14с-12; 4)12m + m; 6)8k+10 k-n?
1377′. Чи треба змінювати знаки доданків у дужках, розкриваючи дужки у виразі:
1)4 + (а+ 3b); 2)-c+(5-d); 3) 16-(5m-8n)?
1378°. Спростіть вираз і підкресліть коефіцієнт:

1379°. Спростіть вираз і підкресліть коефіцієнт:

1380°. Зведіть подібні доданки:
1) 4а – За + 6а – 2а; 4) 10 – 4d – 12 + 4d;
2) 4b – 5b + 4 + 5b; 5) 5а – 12b – 7а + 5b;
3)-7c+ 5-3c + 2; 6) 14n – 12m-4n-3m.
1381°. Зведіть подібні доданки:
1) 6а – 5а + 8а -7а; 3) 5с + 4-2с-3с;
2)9b+12-8-46; 4)-7n + 8m – 13n – 3m.
1382°. Винесіть спільний множник за дужки:
1)1,2а +1,2b; 3) -3n – 1,8m; 5)-5p + 2,5k-0,5t;
2) 0,5с + 5d; 4) 1,2n – 1,8m; 6)-8р – 10k – 6t.
1383°. Винесіть спільний множник за дужки:
1) 6а-12b; 3)-1,8n-3,6m;
2) -0,2с + 1 4d; А) 3р – 0,9k + 2,7t.
1384°. Розкрийте дужки і зведіть подібні доданки;
1) 5 + (4а -4); 4) -(5c-d) + (4d + 5с);
2) 17х-(4х-5); 5) (n – m)- (-2m – 3n);
3) (76 – 4) – (46 + 2); 6) 7(-5х + у) – (-2у + 4х) + (х – 3у).
1385°. Розкрийте дужки і зведіть подібні доданки:
1) 10а + (4 – 4а); 3) (с – 5d) – (-d + 5с);
2) -(46- 10) + (4- 56); 4)-(5n + m) + (-4n + 8m)-(2m-5n).
1386°. Розкрийте дужки і знайдіть значення виразу:
1)15+(-12+ 4,5); 3) (14,2-5)-(12,2-5);
2) 23-(5,3-4,7); 4) (-2,8 + 13)-(-5,6 + 2,8) + (2,8-13).
1387°. Розкрийте дужки і знайдіть значення виразу:
1) (14- 15,8)- (5,8 + 4);
2)-(18+22,2)+ (-12+ 22,2)-(5- 12).
1388°. Розкрийте дужки:
1)0,5 ∙ (а + 4); 4) (n – m) ∙ (-2,4p);
2)-с ∙ (2,7-1,2d); 5)3 ∙ (-1,5р + к – 0,2t);
3) 1,6 ∙ (2n + m); 6) (4,2p – 3,5k-6t) ∙ (-2а).
1389°. Розкрийте дужки:
1) 2,2 ∙ (х-4); 3)(4c-d)∙(-0,5y);
2) -2 ∙ (1,2n – m); 4)6- (-р + 0,3k – 1,2t).
1390. Спростіть вираз:
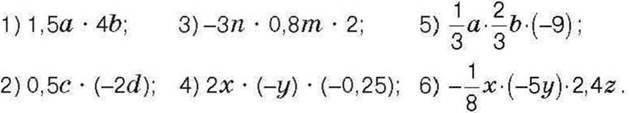
1391. Спростіть вираз:
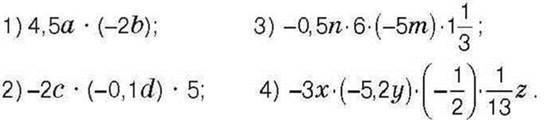
1392. Зведіть подібні доданки:
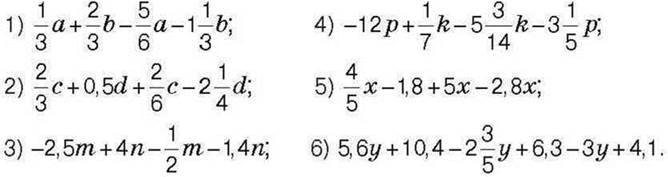
1393. Зведіть подібні доданки:
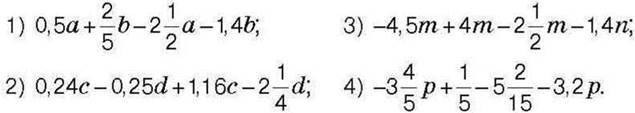
1394. Спростіть вираз:
1)2,8 – (0,5а + 4) – 2,5 ∙ (2а – 6);
2) -12 ∙ (8 – 2,by) + 4,5 ∙ (-6y – 3,2);
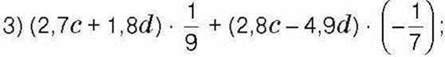
4) (-12,8m + 24,8n) ∙ (-0,5)-(3,5m-4,05m) ∙ 2.
1395. Спростіть вираз:
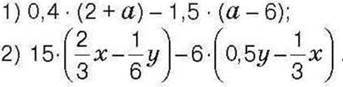
1396. Знайдіть значення виразу;
1) 4-(0,2а-3)-(5,8а-16), якщо а = -5;
2) 2-(7-56)+ 156-3∙(26+ 5), якщо = -0,8;
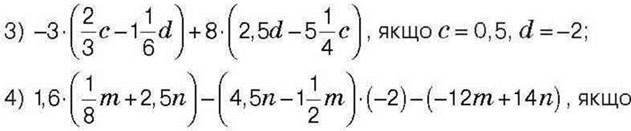
M = 0,25, n = 5,7.
1397. Знайдіть значення виразу:
1) -4∙ (я-2) + 2∙(6x – 1), якщо х =-0,25;
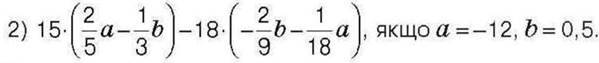
1398*. Знайдіть помилку в розв’язанні:
1)5- (а-2,4)-7 ∙ (-а+ 1,2) = 5а – 12-7а + 8,4 = -2а-3,6;
2) -4 ∙ (2,3а – 6) + 4,2 ∙ (-6- 3,5а) = -9,2а + 46 + 4,26 – 14,7а = -5,5а + 8,26.
1399*. Розкрийте дужки та спростіть вираз:
1) 2аb – 3(6(4а – 1) – 6(6 – 10а)) + 76;
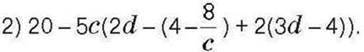
1400*. Розставте дужки так, щоб отримати правильну рівність:
1)а-6-а + 6 = 2а; 2)a-2b-2a + b = 3a-3b.
1401*. Доведіть, що для будь-яких чисел а і b, якщо а > b, то виконується рівність:
1) (а + b) + (а-b) = 2а; 2) (а + b) – (a-b) = 2b.
Чи буде правильною дана рівність, якщо: а) а < b; б) а = 6?
1402*. Доведіть, що для будь-якого натурального числа а середнє арифметичне його попереднього і наступного за ним чисел дорівнює числу а.
ЗАСТОСУЙТЕ НА ПРАКТИЦІ
1403. Для приготування фруктового десерту для трьох осіб потрібно: 2 яблука, 1 апельсин, 2 банани й 1 ківі. Як скласти буквений вираз для визначення кількості фруктів, необхідних для приготування десерту для я гостей? Допоможіть Марин ці підрахувати, скільки фруктів потрібно придбати, якщо до неї в гості завітають: 1) 5 друзів; 2) 8 друзів.
1404. Складіть буквений вираз для визначення часу, необхідного для виконання домашнього завдання з математики, якщо:
1) на розв’язування задач витрачено а хв; 2) на спрощення виразів – у 2 рази більше, ніж на розв’язування задач. Скільки часу виконував домашнє завдання Василько, якщо на розв’язування задач він витратив 15 хв?
1405. Обід у шкільній ‘їдальні складається із салату, борщу, голубців і компоту. Вартість салату становить 20 %, борщу – 30 %, голубців – 45 %, компоту – 5 % загальної вартості всього обіду. Складіть вираз для знаходження вартості обіду в шкільній їдальні. Скільки коштує обід, якщо ціна салату – 2 грн?
ЗАДАЧІ НА ПОВТОРЕННЯ
1406. Розв’яжіть рівняння: 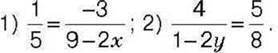
1407. На морозиво Тетянка витратила 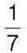 всіх наявних грошей, а на цукерки –
всіх наявних грошей, а на цукерки – 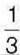 решти. Скільки грошей залишилось у Тетянки,
решти. Скільки грошей залишилось у Тетянки,
Якщо цукерки коштують 12 грн?