Хвильові властивості частинок. Формула де Бройля
ФІЗИКА
Частина 5 АТОМНА ФІЗИКА
Розділ 16 ХВИЛЬОВІ ВЛАСТИВОСТІ РЕЧОВИНИ
16.1. Хвильові властивості частинок. Формула де Бройля
Теорія Бора, пояснивши механізм утворення спектральних ліній і наявність закономірностей у спектрі атома гідрогену і гідрогеноподібних йонів, передбачивши існування раніше невідомих серій в інфрачервоній частині спектра атома гідрогену і діставши більш точні значення в оцінюванні розмірів атома гідрогену, створила тим самим передумови на шляху пояснення будови атомів і характеру протікання внутрішньоатомних
Усі ці недоліки усунуто в квантовій механіці, яка грунтується на докорінній зміні наших уявлень про природу матеріальних частинок. Першим кроком до створення нової квантової теорії стала гіпотеза про існування глибокої аналогії між властивостями світла і властивостями матеріальних частинок, висловлена 1924 р. французьким фізиком Л. де Бройлем. Подібно до того як в одних умовах виявляються корпускулярні властивості світла (як потоку частинок-фотонів), а в інших – хвильові, то й частинки речовини в певних умовах (у мікроявищах) можуть також виявляти хвильові властивості.
Ще в 20-х роках XIX ст. У. Гамільтон довів, що узагальнені закони геометричної оптики й механіки І. Ньютона можна описати рівняннями, математична форма яких тотожна: всі закони геометричної оптики можуть бути виведені з варіаційного принципу П. Ферма, а закони механіки – з варіаційного принципу найменшої дії. Це означає, що для визначення траєкторії матеріальної точки в полі з потенціалом U (х, у, z) можна скористатися рішенням математично подібної задачі на визначення ходу світлових променів у оптично неоднорідному середовищі з відповідно підібраним показником заломлення.
Проте застосування геометричної оптики обмежено випадками, коли розміри отворів, крізь які проходять промені, або розміри перешкод на шляху променів великі порівняно з довжиною їхньої хвилі.
Більш загальною і точною є хвильова оптика, що пояснює закономірне дифракційне відхилення світлових променів від прямолінійності при малих розмірах екранів і отворів, а також явища інтерференції, поляризації тощо. Відкриття квантової природи світла показало, що особливості світла не вичерпуються його хвильовими властивостями. Виявилось, що хвильову оптику треба доповнити аналізом таких випадків, коли проявляються корпускулярні властивості своєрідних світлових частинок – фотонів.
Глибока математична аналогія між ньютонівською механікою і геометричною оптикою дала змогу дійти висновку, що закони квантової механіки аналогічні законам хвильової оптики. У 1924-1926 рр. фізики услід за Л. де Бройлем і Е. Шредінгером переконалися у тому, що, описуючи закони руху найдрібніших частинок речовини, слід користуватися рівняннями, подібними до рівнянь хвильової оптики. Незабаром правильність цієї думки було підтверджено: рух електронів, протонів, атомів тощо керується законами, які є наслідком хвильових процесів. Так виникла хвильова (квантова) механіка, що описує явища в мікросвіті. Механіка І. Ньютона (порівняно з більш загальною хвильовою механікою) є граничним випадком, придатним лише для аналізу руху макроскопічних тіл зі швидкостями υ ” с. Л. де Бройль обгрунтував припущення, що рух кожної частинки супроводжується хвильовим процесом, довжина хвилі якого λ пов’язана з масою m і швидкістю частинки υ простим співвідношенням (формула де Бройля):

Де h – стала Планка.
Формулу де Бройля (16.1) можна застосувати до будь-якої частинки незалежно від ступеня її складності. Проте хвильові властивості частинок виявляються не завжди. Це пов’язано з тим, що довжина хвилі де Бройля λ обернено пропорційна масі частинки. Для макротіл, тобто тіл великої маси, довжина хвилі дуже мала, і хвильовими властивостями таких тіл можна нехтувати. Проте їх не можна не враховувати при розгляді мікрочастинок. Кількісна зміна маси тіла призводить до появи якісно нових хвильових властивостей, які не притаманні макротілам. Наведені особливості свідчать про те, що закони, яким підлягають макротіла, не можна автоматично переносити на мікросвіт. Із співвідношення де Бройля випливає, що довжина хвилі для певного сорту частинок (m = const) залежить від їхньої швидкості. При однакових швидкостях довжина хвилі залежить від маси частинки т. У знаменнику формули (16.1) стоїть імпульс частинки, його можна записати так:
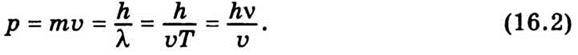
Зазначимо, що де Бройлю вдалося деякою мірою обгрунтувати постулат Бора про стаціонарні орбіти. Для цього він припустив, що стаціонарними є такі стани електронів у атомі, коли на довжині їхньої орбіти вкладається ціле число дебройлівських довжин хвиль. Отже, умова стаціонарних орбіт, за де Бройлем, визначатиметься співвідношенням

Звідки можна дістати співвідношення
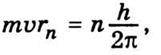
Тобто умову стаціонарності електронних орбіт за Бором (15.11).