Застосування розв’язування трикутників у прикладних задачах
УРОК № 11
Тема. Застосування розв’язування трикутників у прикладних задачах
Мета уроку: формування вмінь учнів застосовувати знання розв’язування трикутників до розв’язування прикладних задач.
Тип уроку: комбінований.
Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника” [13], таблиця 2, посібник [14].
Вимоги до рівня підготовки учнів: розв’язують трикутники. Застосовують алгоритми розв’язування трикутників до розв’язування прикладних задач.
Хід уроку
І. Перевірка
Перевірити наявність виконаних домашніх завдань та відповісти на запитання, які виникли в учнів при виконанні домашнього завдання.
Задача 1. Розв’язання
? = 180°- ? – ? = 180° – 64° – 48° = 68°.
; 
; 
; 
;
; 
; 
;
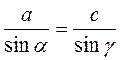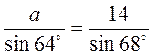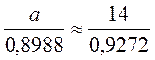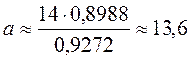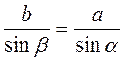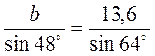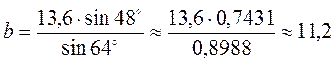Відповідь. ? = 68°, а = 13,6, b = 11,2.
Задача 2. Розв’язання
B2 = a2 + c2 – 2ac cos?; b2 = 576 + 324 – 2 • 24 • 18 • cos15° 
900 – 864 • 0,9659 = 65,4624; b 8,09.
;
; 
; 
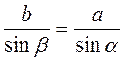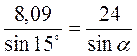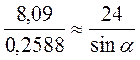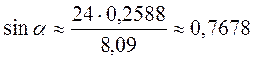; ? 50°.? = 180° – ? – ? 180° – 50° – 15° = 115°.
Відповідь. b 8,09, ? 50°, ? 115°.
Задача 3. Розв’язання
A2 = b2 + c2 – 2bc cos?; 3025 = 441 + 1444 – 1596 cos?; cos? =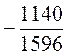 
– 0,7143; ? 136°.
; 
; 
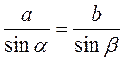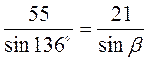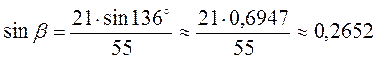; ? 15°.
? = 180° – ? – ? 180° – 136° – 15° = 29°.
Відповідь. ? 136°, ? 15°, ? 29°.
Задача 4. Розв’язання
B2 = a2 + c2 – 2ac cos?; b2 =1024 + 529 – 2 • 32 • 23 • cos152° 1553 – 1472 • (-0,8829) = 1553 + 1299,6288 = 2852,6288; b 53,4.
; 
; 
; 
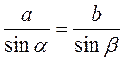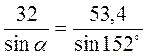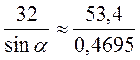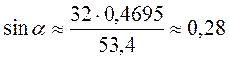; ? 16°.
? = 180° – ? – ? 180° – 16° – 152° = 12°.
Відповідь. b 53,4, ? 16°, ? 12°.
II. Узагальнення й систематизація теоретичних
Фронтальна бесіда
Учні, користуючись табл. 2, дають відповіді на запитання.
1) Сформулюйте теорему косинусів. 2) Поясніть, як із формули a2 = b2+ c2 – 2bc cos? знайти cos?. 3) Як можна визначити вид трикутника (за кутами), якщо відомі сторони а, b, с? 4) Сформулюйте теорему синусів. 5) Сформулюйте теорему про співвідношення між кутами трикутника і протилежними сторонами. 6) Сформулюйте теорему про співвідношення між сторонами трикутника і протилежними кутами. 7) Як можна знайти радіус кола, описаного навколо трикутника, у якому відомі сторона і протилежний кут? 8) Які є основні випадки розв’язування довільних трикутників?
Таблиця 2
Теорема косинусів
A2 = b2 + c2 – 2bc cos?;
B2 = a2 + c2 – 2ac cos?;
С2 = a2 + b2 – 2ab cos?
Теорема синусів
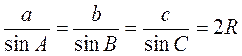
Теорема про суму кутів трикутника
? + ? + ? = 180°
Розв’язування трикутників
1. Дано: а, ?, ?. Знайти: b, с, ?.
Розв’язання
1) ? = 180° – (? + ?);
2) ; 
;
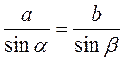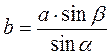3) ; 
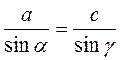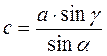
2. Дано: а, b, ?. Знайти: с, ?, ?.
Розв’язання
1) c =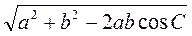 
;
2) 
; 
;
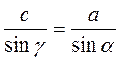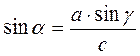3) ? = 180° – (? + ?)
3. Дано: а, b, ?. Знайти: с, ?, ?.
Розв’язання
1) ; 
;
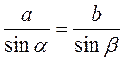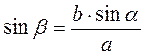2) ? = 180° – (? + ?);
3) ;
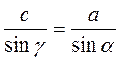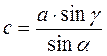
4. Дано: а, b, с. Знайти: ?, ?, ?.
Розв’язання
1) a2 = b2 + c2 – 2bc cos?;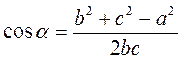 
2) ; 
;
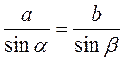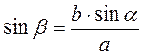3) ? = 180° – (? + ?)
ІІІ. Формування вмінь учнів застосовувати знання з розв’язування трикутників до розв’язування
Розв’язування задач
1. Дві сили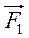 
і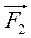 
утворюють кут?. Знайдіть їх рівнодійну, якщо:
А) F1 = 8,6 Н, F2 = 6,5 Н, ? = 130°;
Б) F1 = 9,7 Н, F2 = 10,8 H, ? = 75°.
(Відповідь, а) 6,7 Н; б) 16,3 Н.)
2. Рівнодійна двох сил 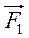і 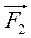дорівнює 
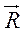. Знайдіть кут між силами 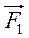і 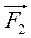, якщо:
А) F1 = 62 Н, F2 = 50 Н, R = 47 Н;
Б) F1 = 6,7 Н, F2 = 9,8 Н, R = 12,8 Н.
(Відповідь, а) 132°; б) 80°.)
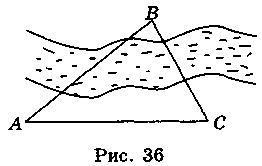
3. Щоб знайти відстань до недоступної точки В від доступної точки, виконали вимірювання (рис. 36):
А) AС = 19 м, 
A = 80°, C = 68°;
Б) АС = 50 м, A = 65°, C = 80°.
Знайдіть відстань АВ.
(Відповідь, а) 33 м; б) 86 м.)
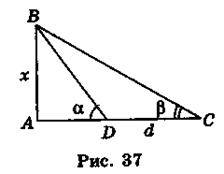
4. Поясніть, як знайти висоту х будівлі (рис. 37) за кутами? і? та відстанню d.
Розв’язання
Нехай DC = d, BDA = ?, BCD = ? (рис. 37), тоді BDC = 180° – ?, DBC = 180° – 180° + ? – ? = ? – ?. Із трикутника BDC маємо: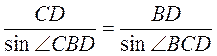 
; 
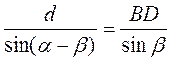, звідси 
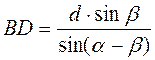. Із трикутника ABD маємо: АВ = BD sinBDA = BD sina =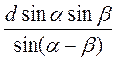 
; 
.
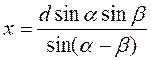Відповідь. .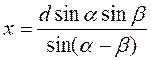
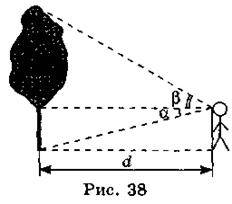
5. Спостерігач перебуває на відстані d від дерева, висоту якого хоче визначити (рис. 38). Основу дерева спостерігач бачить під кутом? до горизонту, а вершину дерева – під кутом? до горизонту. Яка висота дерева?
Відповідь. d(tg? + tg?).
IV. Самостійна робота
Самостійну роботу навчального характеру можна провести, скориставшись посібником [14], тест 4 “Розв’язування трикутників”.
V. Домашнє завдання
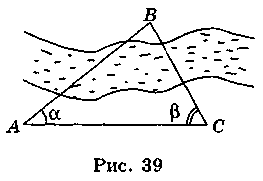
1. Поясніть, як знайти відстань від точки А до недоступної точки В (рис. 39), знаючи відстань АС і кути? і?. 2. Розв’яжіть трикутник: b = 12, ? = 36°, ? = 25°.
VI. Підбиття підсумків уроку
Запитання до класу
1. Що означає розв’язати трикутник? 2. Складіть план розв’язування трикутників, якщо задано:
А) сторону b і два кути? і?;
Б) дві сторони а і b та кут між ними?.
(1 votes, average: 5.00 out of 5)
Loading...