Абсолютно пружний удар
2-й семестр
МЕХАНІКА
3 . Закони збереження в механіці
Урок 11/55
Тема. Абсолютно пружний удар
Мета уроку: продемонструвати учням використання законів збереження енергії та імпульсу для пояснення задач на зіткнення тіл
Тип уроку: комбінований
План уроку
Контроль знань | 15 хв. | Самостійна робота № 1. “Енергія. Закон збереження енергії” |
Демонстрації | 3 хв. | 1. Пружне зіткнення. 2. Непружне зіткнення |
Вивчення | 22 хв. | 1. Види зіткнень. 2. Абсолютно пружний удар. 3. Абсолютно непружний удар. 4. Пружний центральний удар кульок однакової маси. 5. Пружний центральний удар кульок різної маси |
Закріплення вивченого матеріалу | 5 хв. | 1. Тренуємося розв’язувати задачі. 2. Контрольні запитання |
ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ
1. Види зіткнень
Закон збереження механічної енергії та закон збереження імпульсу дозволяють розв’язувати механічні задачі в тих випадках, коли не відомі сили, що діють. Прикладом подібних задач є ударна
O Ударом (або зіткненням) прийнято називати короткочасну взаємодію тіл, у результаті якої їхні швидкості зазнають значних змін.
Під час зіткнення тіл між ними діють короткочасні ударні сили, величина яких зазвичай не відома, тому не можна розглядати ударну взаємодію безпосередньо за допомогою законів Ньютона. Застосування законів збереження енергії та імпульсу в багатьох випадках дозволяє виключити з розгляду власне процес зіткнення й отримати зв’язок між швидкостями тіл до і після зіткнення, минаючи всі проміжні значення цих величин.
З ударною взаємодією тіл нерідко доводиться мати справу в повсякденному житті, у техніці й фізиці. У механіці часто використовуються дві моделі ударної взаємодії – абсолютно пружний та абсолютно непружний удари.
2. Абсолютно пружний удар
O Абсолютно пружний удар – це зіткнення, за якого зберігається механічна енергія системи тіл.
У разі абсолютно пружного удару, крім закону збереження енергії, виконується закон збереження імпульсу.
Простим прикладом абсолютно пружного зіткнення може бути центральний удар двох більярдних куль, одна з яких до зіткнення перебувала в стані спокою.
У багатьох випадках зіткнення атомів, молекул та елементарних частинок підпорядковуються законам абсолютно пружного удару.
Після абсолютно пружного удару в тілах, що взаємодіють, не залишається жодних деформацій, і сумарна кінетична енергія, яку мали тіла до удару, дорівнює кінетичній енергії тіл після удару.
Зіткнення абсолютно пружних тіл (рис. а) відбувається так: під час удару тіла деформуються й виникають сили пружності, які надають прискорення обом тілам у протилежних напрямах (рис. б).
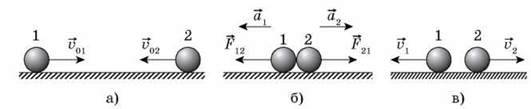
Після цього кульки починають віддалятися одна від одної, а деформації починають зменшуватися, поки не зникнуть остаточно. До цього моменту пружні сили, що виникають у тілах, виконують таку саму роботу, що була витрачена на деформацію. У результаті вся кінетична енергія, яку мали тіла до удару, знову перейде в кінетичну енергію тіл після удару (рис. в).
3. Абсолютно непружний удар
O Абсолютно непружний удар – це зіткнення, за якого тіла з’єднуються (злипаються) одне з одним і рухаються далі як одне тіло.
За абсолютно непружного удару механічна енергія не зберігається. Вона частково або повністю переходить у внутрішню енергію тіл. Закон же збереження імпульсу в цьому випадку виконується.
Прикладом абсолютно непружного удару може бути зіткнення метеорита із Землею; удар під час падіння грудки глини на землю; зіткнення кулі та ящика з піском; захоплення нейтрона ядром атома Урану в процесі ланцюгової ядерної реакції; приєднання електрона до атома в процесі іонізації тощо.
4. Пружний центральний удар кульок однакової маси
Розглянемо найпростіший випадок абсолютно пружного удару – центральне зіткнення двох однорідних кульок.
O Зіткнення (удар) називається центральним, якщо вектори швидкості кульок до і після удару спрямовані вздовж прямої, що проходить через їхні центри.
Нехай дві однакові кульки рухаються назустріч одна одній зі швидкостями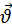 
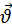10 і 20, спрямованими вздовж лінії, що з’єднує центри кульок (рис. а).
Обчислимо швидкост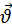і 1 і 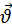2 кульок після удару (рис. б).
Ці кульки можна вважати замкнутою системою, тому що сила тяжіння й сила реакції опори зрівноважують одна одну, а дією сили тертя і втратами енергії у випадку непружних деформацій можна знехтувати. У замкнутій системі виконуються закони збереження імпульсу та енергії.
Запишемо закон збереження імпульсу у векторному вигляді:
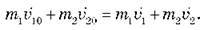
У проекції на вісь Ох це рівняння має вигляд:
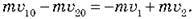
У цьому рівнянні ми врахували, що m1 = m2 = m.
Після скорочення на m маємо: 
10 – 20 = –X + 2.
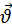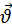Це рівняння містить дві невідомі – 1 і 2.
Скористаємося законом збереження енергії:
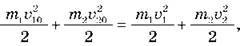
Або, скоротивши:
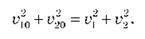
Перегрупувавши складові, отримуємо систему двох рівнянь з двома невідомими:
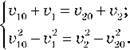
Розклавши ліву й праву частини другого рівняння на складові, дістаємо:
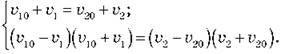
Розділивши почленно друге рівняння системи на перше, отримуємо рівносильну систему:
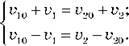
Віднімаючи від першого рівняння друге, маємо:
1 = 20.
Складаючи обидва рівняння, отримуємо:
2 = 10.
Як бачимо, у результаті пружного зіткнення однакові кульки обмінюються швидкостями.
Кулька, що рухається з більшою початковою швидкістю, при цьому вповільнюється, а більш повільна кулька прискорюється, отримуючи енергію.
Якщо одна кулька рухається зі швидкістю 10 = , а друга перебуває в стані спокою 20 = 0, то після зіткнення перша кулька зупиниться, а друга почне рухатися зі швидкістю 2 = .
Унаслідок центрального удару кульок та кулька, що рухалася, зупиняється, а нерухома дістає швидкість кульки, яка рухається.
5. Пружний центральний удар кульок різної маси
Розглянемо взаємодію тіл різної маси. Для простоти вважатимемо, що важча кулька перебуває в стані спокою, а напрям швидкостей кульок після удару виберемо такий, як показано на рисунку.
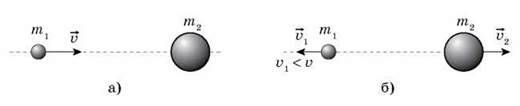
Закон збереження імпульсу в проекції на вісь має вигляд:
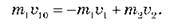
Закон збереження енергії має вигляд:
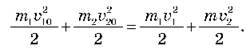
Перемножуючи почленно вирази на 2 і враховуючи, що 20 = 0, дістаємо:
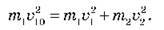
Отже, ми отримали систему двох рівнянь:
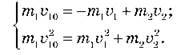
Перегрупуємо складові й винесемо m1 за дужки:
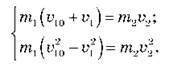
Поділивши почленно друге рівняння на перше, отримуємо рівносильну систему:
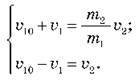
Віднімаючи від першого рівняння друге, отримуємо:
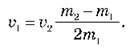
Складаючи рівняння системи, отримуємо:
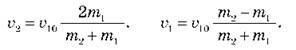
Аналіз рівнянь показує, що після удару легка кулька рухається у зворотному напрямі, а її швидкість менша за початкову.
Запитання до учнів під час викладу нового матеріалу
1. Наведіть приклади абсолютно пружного удару.
2. Наведіть приклади абсолютно непружного удару.
3. Чи виконується під час абсолютно пружного удару закон збереження енергії? закон збереження імпульсу?
4. Чи виконується під час абсолютно непружного удару закон збереження енергії? закон збереження імпульсу?
5. Що можна сказати про швидкості тіл однакової маси після абсолютно пружного удару?
ЗАКРІПЛЕННЯ ВИВЧЕНОГО МАТЕРІАЛУ
1). Тренуємося розв’язувати задачі
1. Який молоток (легкий чи важкий) у процесі кування втрачає більшу частину своєї енергії? Чому?
2. Кулька масою 200 г, що рухається зі швидкістю 4 м/с, зіштовхується з кулькою тієї ж маси, яка рухається назустріч їй зі швидкістю 1 м/с. Уважаючи удар центральним і пружним, обчисліть швидкість кульок після удару.
2). Контрольні запитання
1. Чому гумові балони автомобіля (а також ресори, вагонні буфери) ослабляють поштовхи й удари?
2. Коли куля, що перебуває в стані спокою, отримує більшу швидкість у порівнянні з іншою: під час пружного чи непружного центрального удару?
Що ми дізналися на уроці
– Ударом (або зіткненням) прийнято називати короткочасну взаємодію тіл, у результаті якої їхні швидкості зазнають значних змін.
– Абсолютно пружний удар – це зіткнення, коли зберігається механічна енергія системи тіл.
– Абсолютно непружний удар – це зіткнення, під час якого тіла з’єднуються (злипаються) одне з одним і рухаються далі як одне тіло.
– Зіткнення (удар) називається центральним, якщо вектори швидкості кульок до і після удару спрямовані вздовж прямої, що проходить через їхні центри.
Домашнє завдання
1. П.: § 38.
2. 36.: № 18.70; 18.71; 18.78; 18.79.
(1 votes, average: 5.00 out of 5)
Loading...