Головна ⇒ 📌Математика ⇒ Числові вирази. Буквені вирази та їх значення. Формули

Числові вирази. Буквені вирази та їх значення. Формули

Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ

§ 10. Числові вирази. Буквені вирази та їх значення. Формули

Приклад 1. Поїзд проїхав за першу годину 60 км, а за другу – на 5 км більше. Скільки кілометрів проїхав потяг за дві години?

Розв’язання. За другу годину потяг проїхав 60 + 5 кілометрів.

Тому за дві години він проїхав 60 + (60 + 5) кілометрів.

Для розв’язання задачі ми склали числовий вираз із знаків дій та дужок.

Виконавши дії, отримаємо число 125 – значення цього виразу.

Приклад 2. Поїзд проїхав

за першу годину 60 км, а за другу – на а кілометрів більше. Скільки кілометрів проїхав потяг за дві години?

Розв’язання. Аналогічно до попереднього прикладу отримаємо: за дві години потяг проїхав 60 + (60 + а) кілометрів. Запис 60 + (60 + а) – буквений вираз, який складається із чисел, букв, знаків дій та дужок.

Значення буквеного виразу залежить від значення букви, яка входить до виразу.

Приклад 3. Знайди значення виразу 7 + b, якщо b = 5; 10.

Розв’язання. Якщо b = 5, то 7 + b = 7 + 5 = 12; якщо b = 10, то 7 + b = 7 + 10 = 17.

Отже, вирази, які складаються із чисел, знаків дій та дужок, наприклад:

3547 – 2793, 480 312 – 9279,

7257 –

(8705 – 5744), називають числовими виразами.

Якщо виконати дії в числових виразах, то отримаємо число, яке називають значенням числового виразу.

Вираз, який містить букви, числа, знаки дій та дужки, називають буквеним, наприклад:

А + 400, 504 ∙ а, а : b, (а + b) ∙ с.

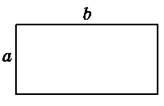
Нехай сторони прямокутника дорівнюють а і b. Позначимо буквою S його площу. Оскільки площа прямокутника дорівнює добутку довжин його сторін, то можна записати:

S = а ∙ b.

Як відомо з молодших класів, периметр прямокутника P дорівнює сумі довжин усіх його сторін. Оскільки протилежні сторони прямокутника рівні між собою, то

Р = а ∙ 2 + b ∙ 2, або Р = (а + b) ∙ 2.

Наведені рівності справедливі при всіх значеннях букв, що до них входять. Їх називають формулами.

Формула – це запис деякого правила за допомогою букв, що встановлює взаємозв’язок між величинами.

Формули допомагають обчислити значення однієї з величин за відомими значеннями решти величин. Наприклад, з формули площі прямокутника маємо: a = S : b, b = S : а.

Щоб знайти сторону прямокутника, треба його площу поділити на іншу сторону.

Нехай v – швидкість руху, t – час руху і s – пройдена відстань (шлях). Рівність s = v ∙ t, яка встановлює залежність між цими величинами, називається формулою шляху. Формула шляху означає, що відстань дорівнює швидкості, помноженій на час:

S = v ∙ t.

З формули шляху за правилом знаходження невідомого множника маємо: v = s : t, t = s : v.

– Швидкість дорівнює відстані, поділеній на час.

– Час руху дорівнює відстані, поділеній на швидкість.

Початковий рівень

330. (Усно). Назви числові, буквені вирази і формули серед таких виразів:

1) 525 + 137; 2) m + 54; 3) s = vt;

4) 42 – (31 – 18); 5) x = 2m + 3; 6) х + у – 3.

331. Сергій мав а моделей машинок. На день народження йому подарували 15 машинок. Скільки машинок стало у Сергія?

332. До магазину привезли а кг бананів. За день продали 215 кг. Скільки кілограмів бананів залишилося в магазині?

333. У 5-А класі навчається 30 учнів. За урок з трудового навчання кожен учень виготовив по х вітальних листівок. Скільки вітальних листівок виготовив клас за урок?

Середній рівень

334. Обчисли значення виразу 312 + а, якщо а = 12; 289.

335. Обчисли значення виразу m + (n – 8), якщо m = 10; n = 12.

336. Знайди значення виразу:

1) x + 3117, якщо x = 2173; 989;

2) 4117 : у, якщо у = 23; 179;

3) m – n, якщо m = 12 179; n = 8397;

4) (а + b) ∙ с, якщо а = 113; b = 227; с = 13.

337. Заповни таблицю.

M	327	1213	82 321	5221
N	159	987	3327	0
M + n
M – n

338. Обчисли за формулою периметр квадрата, сторона якого має довжину 7 см, 8 дм.

339. Обчисли значення у за формулою y = 8х + 7, якщо х = 0, 1, 25, 100.

340. Знайди, використовуючи формулу шляху s = v ∙ t:

1) час, за який автомобіль проїде 312 км зі швидкістю 78 км/год;

2) швидкість мотоцикліста, який проїхав 272 км за 4 год.

341. За формулою шляху s = vt обчисли відстань, яку проїде автомобіль, що рухається 5 год зі швидкістю 102 км/год.

Достатній рівень

342. Запиши рівності, заповнивши клітинки:

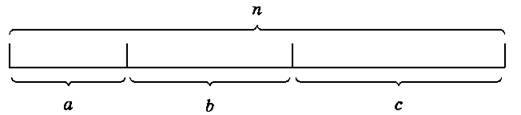
1) n = □ + □ + □; 2) с = □ – □ – □;

З) а + с = □ – □; 4) n – a = □ + □.

343. Склади вираз, щоб знайти невідому величину х.

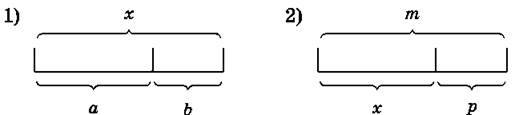
344. На склад привезли 42 ящики, у кожному з яких по 25 кг яблук, і 54 ящики, у кожному з яких по 32 кг яблук. Склади числовий вираз для обчислення маси всіх завезених яблук та знайди його значення.

345. Турист проїхав на велосипеді 60 км за 5 год та пройшов пішки 15 км за 3 год. На скільки швидкість туриста на велосипеді більша, ніж пішки? Запиши розв’язок у вигляді числового виразу та знайди його значення.

346. Склади числові вирази і знайди значення кожного з них:

1) різниця суми чисел 325 і 733 та числа 812;

2) добуток різниці чисел 215 і 199 та суми чисел 95 і 72.

347. Склади буквений вираз:

1) від числа m відняти суму чисел а і b;

2) різницю чисел р і k збільшити в f разів;

3) до числа с додати частку чисел d і n;

4) суму чисел f і q зменшити в w разів.

348. Автомобіль перші а годин їхав зі швидкістю 70 км/год, а потім – b годин зі швидкістю 80 км/год. Склади вираз для обчислення шляху, що подолав автомобіль. Обчисли значення виразу, якщо а = 3, b = 4.

349. За перший день магазин продав 1300 зошитів, за другий – на x зошитів менше. Склади вираз для обчислення кількості зошитів, які продав магазин за два дні, та обчисли його значення, якщо х = 211.

350. У Івана x цукерок, а в Сергія – у цукерок. Вони склали їх і поділили порівну. Скільки цукерок отримав кожен хлопець? Склади вираз і знайди його значення, якщо x = 9, у = 13.

351. Нехай Р – периметр прямокутника, а і b – його сторони. Запиши формулу для обчислення периметра прямокутника. Знайди Р, якщо а = 12 см, b = 3 дм.

352. Одна сторона трикутника дорівнює а сантиметрів, а дві інші – по b сантиметрів. Запиши вираз для обчислення периметра P трикутника та знайди його значення, якщо а = 8, b = 7.

353. Заповни таблицю.

S	252 км	238 м	3 км	60 000 м
V	10 км/год	34 м/с	10 м/с	9 км/год	15 км/год
T	7 год	4 год	2 хв

354. Заповни таблицю.

S	432 км	15 000 м
V	15 м/хв
T	9 год	2 год	5 год

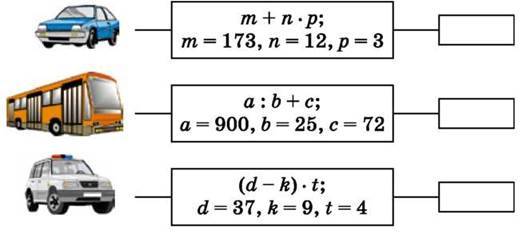
355. Яка з машин проїхала більшу відстань? Значення виразу – це відстань (у кілометрах), що проїхала машина.

Високий рівень

356. Буратіно має m сольдо, Арлекіно n сольдо, а Мальвіна k сольдо. Що означають вирази:

1) m + n; 2) n – k; 3) m + n + k;

4) (m + n) – k; 5) m – (n + k); 6) m : k?

357. Хлопчик мав 18 грн. і купив х зошитів по 1 грн. 30 коп. кожний. Склади формулу для обчислення грошей, що залишилися у хлопчика, та обчисли, якщо х = 9.

358. Майстер Самодєлкін за t хв виготовив одну складну деталь та три прості деталі. На виготовлення складної деталі він затратив 15 хв. Скільки часу затратив Самодєлкін на виготовлення однієї простої деталі? Склади буквений вираз і знайди його значення, якщо t = 33.

359. В одній пачці було 20 зошитів, у другій – на x зошитів менше, а в третій – удвічі більше, ніж у другій. Скільки зошитів було в трьох пачках разом? Склади буквений вираз та обчисли його значення, якщо x = 2.

360. Натуральне число позначено буквою а. Запиши:

1) наступне число; 2) попереднє число.

361. Натуральне число позначено b + 1. Запиши: 1) три наступні числа; 2) два попередні числа.

Вправи для повторення

362. Накресли відрізок АВ завдовжки 7 см. Познач на ньому точку D. Виміряй довжину утворених відрізків AD і DB.

363. Вирази в кілограмах:

1) 3000 г; 2) 15 000 г;

3) 3 т; 4) 3 т 210 кг;

5) 9 ц; б) 9 ц 5 кг.

364. Склади умови задач за схемами. Розв’яжи їх.