ЧИСЛОВІ ВИРАЗИ, РІВНОСТІ, НЕРІВНОСТІ. ПОРІВНЯННЯ НАТУРАЛЬНИХ ЧИСЕЛ
РОЗДІЛ 1
ЛІЧБА, ВИМІРЮВАННЯ І ЧИСЛА
§ 4. ЧИСЛОВІ ВИРАЗИ, РІВНОСТІ, НЕРІВНОСТІ. ПОРІВНЯННЯ НАТУРАЛЬНИХ ЧИСЕЛ
Ви вже знаєте чотири арифметичні дії над числами – додавання, віднімання, множення і ділення. Щоб записати, яку саме дію над числами треба виконати, використовують числові вирази. Наприклад, записи 24 + 2, 24 – 2, 24 ∙ 2, 24 : 2 є числовими виразами.
Запис, в якому використовують тільки числа, знаки арифметичних дій і дужки, називається числовим виразом.
Числовий вираз показує, яку арифметичну дію треба виконати над числами,
Вираз 24 + 2 називається сумою чисел 24 і 2.
Вираз 24-2 називається різницею чисел 24 і 2.
Вираз 24 ∙ 2 називається добутком чисел 24 і 2.
Вираз 24 : 2 називається часткою чисел 24 і 2.
Числа 24 і 2 в кожному із цих числових виразів називаються компонентами виразу.
Зверніть увагу:
щоб прочитати числовий вираз, спочатку прочитайте його назву, а потім його компоненти.
Число, яке дістанемо в результаті виконання арифметичної дії у виразі, називається значенням числового виразу. Наприклад, значенням суми чисел 24 і 2 є число 26, а значенням добутку чисел 24 і 2 є число 48.
Якщо числовий
Два числових вирази, що мають рівні значення, можна прирівняти. Для цього сполучимо їх знаком рівності. Отриманий запис теж є числовою рівністю. Наприклад, 24 + 2 = 13 ∙ 2 і 24 – 2 = 44 : 2.
Запис, у якому два числа, або два числових вирази, або числовий вираз і число сполучено знаком рівності, називається числовою рівністю.
? Чи можна прирівняти числові вирази 24 + 2 і 24 ∙ 2? Ні, бо значення цих виразів не дорівнюють одне одному.
Коротко записують: 24 + 2 ≠24 ∙ 2. Знак означає “не дорівнює”.
Зверніть увагу:
1) числова рівність показує результат порівняння – два числа дорівнюють одне одному;
2) запис, що містить знак “≠”, не є числовою рівністю.
Із двох різних натуральних чисел завжди одне число є більшим, а друге меншим. Наприклад, 9 більше за 4, відповідно, 4 менше від 9.
Коротко записують: 9 > 4 або 4 < 9. Знаки “>” і “<” означають відповідно “більше” і “менше”. Такі знаки називаються знаками нерівності.
Знаком нерівності можна сполучити не тільки два числа, а й два числових вирази, якщо їх значення не дорівнюють одне одному і відомо, яке з них є більшим, а яке – меншим. Наприклад, 4 + 2 < 4 ∙2. Аналогічно, знаком нерівності можна сполучити числовий вираз і число. Наприклад, 4 + 2 > 5
Запис, у якому два числа, або два числових вирази, або числовий вираз і число сполучено знаком нерівності, називається числовою нерівністю.
? Чи є числовою нерівністю запис 4 + 2 ≠ 4 ∙ 2? Ні, оскільки з такого запису не ясно, який числовий вираз має більше значення, а який менше.
Зверніть увагу:
1) числова нерівність показує результат порівняння – яке із чисел більше, а яке менше;
2) запис, що містить знак “≠”, не є числовою нерівністю.
Числа можна порівнювати за допомогою координатного променя. Із двох чисел більшим є те число, яке на координатному промені розміщується далі від його початку. На малюнку 61 координатний промінь зображено горизонтально. Тому про розміщення двох чисел на ньому можна сказати: одне число розміщується “правіше” або “лівіше” від іншого. Ви бачите, що число 10 розміщено правіше від числа 7, тому 10 > 7 або 7 < 10.

Мал. 61
Подивіться на малюнок 62. Ви бачите, що на координатному промені число 6 розміщується між числами 3 і 8. Зрозуміло, що 6 > 3 і 6 < 8. Разом це можна записати у вигляді подвійної нерівності: 3 < 6 < 8. Числа 3 і 8 називаються крайніми членами подвійної нерівності, а число 6 – середнім членом подвійної нерівності.

Мал. 62
Подвійну нерівність 3 < 6 < 8 читають, починаючи із середнього члена: “Число 6 більше за 3 і менше від 8”.
На малюнку 62 ви бачите, що між числами 3 і 8, крім числа 6, розміщуються й інші натуральні числа. Це
Числа 4, 5 і 7. Тому для крайніх членів 3 і 8 правильними є і такі подвійні нерівності:
З < 4 < 8; 3 < 5 < 8; 3<7<8.
Для порівняння багатоцифрових чисел користуються спеціальними правилами. Розглянемо приклади.
Задача. Порівняйте числа: у 1)96 і 830; 2) 3574 і 3547.
Розв’язання. 1. Число 96- двоцифрове, а число 830 – трицифрове, тому 96 < 830.
2. У записах чисел 3574 і 3547 та сама кількість цифр. Тому їх краще порівнювати порозрядно. Для цього запишемо дані числа одне під одним: 3574
3547
Кожне із чисел має 3 тисячі і 5 сотень. Але у першому числі є 7 десятків, а у другому – лише 4 десятки. Тому перше число і є більшим за друге: 3574 > 3547.
Правила порівняння багатоцифрових чисел.
1. Із двох натуральних чисел більшим є те число, у запису якого цифр більше.
2. Якщо у запису двох натуральних чисел та сама кількість цифр, то числа порівнюють порозрядно, починаючи із найстаршого розряду.
Дізнайтеся більше
1. Знак рівності “=” увів англійський учений Роберт Рекорд у 1557 році. На його думку, ніщо не може передати рівність так, як два паралельних відрізки однакової довжини. До нього в математиці користувалися іншими знаками рівності. Так, давньогрецький математик Діофант відношення рівності позначав літерою “і”, яка є першою буквою грецького слова “σωξ” – рівний. Індійські та арабські математики, а також більшість європейських, найчастіше, аж до XVII століття, рівність позначали словесно “est egale”. Р. Бомбеллі (1572 р.) позначав рівність буквою “а”, котра є першою в латинському слові “aequalis” – рівний.
2. Знаки “>” і “<” ввів Томас Герріот в своєму творі “Застосування аналітичного мистецтва до розв’язування алгебраїчних рівнянь”, виданому посмертно в 1631 році. До нього писали словами: більше, менше.
РОЗВ’ЯЖІТЬ ЗАДАЧІ
106. Прочитайте числові вирази, використовуючи терміни “сума”, “різниця”, “добуток” і “частка”:
1)435 + 340; 3)45 ∙ 32;
2) 127 – 102; 4)2460:12.
107. Чи можна прирівняти числові вирази:
1) 25 + 4 і 25 ∙ 4; 3) 30 – 15 і 30 + 15; 5) 14 + 0 і 14 – 0;
2) 2 + 2 і 2 ∙ 2; 4)2-1 і 2: 1; 6) 28 – 1 і 28 : 1 ?
Відповідь поясніть.
108. Прочитайте числові нерівності:
1)345 <405; 2) 172 >100; 3) 296 < 504.
109. Назвіть два натуральні числа, які лежать на координатному промені:
1) правіше від числа 36; 2) лівіше від числа 36.
Порівняйте названі числа із числом 36.
110. Прочитайте подвійні числові нерівності:
1)64 <80 <91; 3) 254 < 255 < 256;
2) 304 <381 <392; 4) 99 < 100 < 101.
Назвіть крайні і середній члени нерівності.
111. Назвіть найбільше і найменше трицифрові числа, які більші за число 342. Назвіть найбільше й найменше трицифрові числа, менші відданого числа.
112. Запишіть числовий вираз та обчисліть його значення:
1) сума числа 152 та добутку чисел 45 і 21;
2) різниця суми чисел 245 і 197 та числа 45;
3) добуток суми чисел 452 і 148 та числа 12;
4) частка числа 625 та різниці чисел 100 і 75.
113. Запишіть числовий вираз та обчисліть його значення:
1) сума добутку чисел 28 і 15 та числа 120;
2) добуток числа 35 та різниці чисел 506 і 468.
114. Складіть числовий вираз для розв’язування задачі та знайдіть його значення.
Довжина відрізка АВ дорівнює 15 см. Довжина відрізка CD у 3 рази менша від довжини відрізка АВ. Знайдіть довжину відрізка MN, якщо вона дорівнює різниці довжин відрізків АВ і CD.
115. Складіть числовий вираз для розв’язування задачі та знайдіть його значення.
Довжина відрізка АВ дорівнює 5 см. Довжина відрізка CD у 2 рази більша за довжину відрізка АВ. Знайдіть довжину відрізка MN, якщо вона дорівнює сумі довжин відрізків АВ і CD,
116. Запишіть числову нерівність:
1) 25 менше від 72;
2) 56 більше за 43;
3) 38 більше за 12, але менше від 60.
Як розміщуються дані числа на координатному промені?
117. Запишіть числову нерівність:
1) 30 менше від 53;
2) 124 більше за 95;
3) 201 більше за 200 і менше від 202;
4) 67 більше за 45, але менше від 102.
Як розміщуються дані числа на координатному промені?
118. На координатному промені (мал. 63) назвіть число, що розміщується: 1) на 5 одиниць лівіше від числа 5; 2) на 4 одиниці правіше від числа 5; 3) між числами 5 і 12. Запишіть відповідні числові нерівності.

Мал. 63
119. На координатному промені (мал. 64) назвіть число, що розміщується:
1) на 4 одиниці правіше від числа 6;
2) між числами 6 і 11.
Запишіть відповідні числові нерівності.

Мал. 64
123. Порівняйте:
1) 20 см і 25 см; 3)1 м і 100 см;
2) 50 см і 50 мм; 4)12дм і 24см.
124. Порівняйте:
1) 45 хв і 15 хв; 3) 60 хв і 1 год;
2) 15 хв і 15 с; 4) 75 хв і 1 год.
122. Порівняйте числа:
1)345 і 2354; 3)120980 і 128900;
2)2456 і 2465; 4)15999 і 16001.
123. Порівняйте числа:
1)2390 і 987; 3)178099 і 200000;
2)25756 і 25134; 4)5000000 і 3111111.
124. Розташуйте в порядку зростання числа:
346, 10087, 34, 99456, 43, 10098, 200000.
125. Розташуйте в порядку спадання числа:
1256, 88, 167, 40256, 809, 340340, 560000.
126. Складіть і запишіть три числових вирази, які мають одне й те саме значення, що дорівнює 25.
127. Запишіть будь-який числовий вираз, для обчислення значення якого необхідно послідовно виконати дії:
1) додавання, множення і віднімання;
2) множення, додавання, ділення і віднімання.
128. Яке найбільше натуральне число можна поставити замість зірочки, щоб отримати правильну числову нерівність:
1) * < 17; 2) *<14?
Як розміщуються дані числа на координатному промені?
129. Яке найменше натуральне число можна поставити замість зірочки, щоб отримати правильну числову нерівність:
1) * < 75; 2) *>56?
Як розміщуються дані числа на координатному промені?
130. Запишіть усі натуральні числа, які можна поставити замість зірочки, щоб отримати правильну числову нерівність:
1) 238 < * < 241; 2) 19090 <*< 19100.
131. Чи можна порівняти наступні числа, якщо одна зірочка замінює одну цифру в запису числа:
1)37* і 39*; 3) *5* і *9*;
2)1 ** i 9*; 4) 292* і 2*099?
Відповідь поясніть.
132. Ганнуся купила 2 морозива та 1 тістечко і заплатила 4 грн 50 к. Якби вона купила 1 морозиво та 2 тістечка, то заплатила б 6 грн. Скільки коштує морозиво і скільки коштує тістечко?
133. Старовинна задача. Торговець продав одному покупцеві 10 яблук, 5 груш і 3 лимони за 1 карбованець 10 копійок, другому покупцеві за тією самою ціною він продав 10 яблук, 3 груші і 1 лимон за 78 копійок, а третьому 2 груші і 1 лимон за 22 копійки. Скільки коштують окремо яблуко, груша і лимон?
Застосуйте на практиці
134. Дмитрик старший за Василька, але молодший від Сергійка. Сашко старший за всіх. Назвіть хлопчиків від наймолодшого до найстаршого.
135. Порівняйте:
1) що складніше: пробігти 1 км чи 1000 м;
2) що важче; підняти 5 кг чи 500 г;
3) що довше: очікувати 2 год чи 100 хв?
ЗАДАЧІ НА ПОВТОРЕННЯ
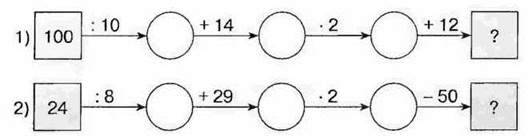
136. Обчисліть усно, яке число треба вписати в останню клітинку ланцюга:
137. Обчисліть:
1) 10486 : (455-357)+ 49 ∙ 12; 2) (52 ∙15+ 120)-840: 12.
138. У Тетянки 14 цукерок, у Марічки – на 4 цукерки менше, ніж у Тетянки, а у Софійки – у 2 рази більше, ніж у Марічки. Скільки всього цукерок у дівчат?
139. Туристи за 3 дні подолали 48 км. Першого дня вони пройшли 8 км, другого дня проїхали на автобусі відстань, у 3 рази більшу, ніж за перший день. Скільки кілометрів залишилося пройти туристам третього дня?