Головна ⇒ 📌Довідник з математики ⇒ Дійсні числа
Дійсні числа
Математика – Алгебра
Квадратні корені
Раціональні числа – це числа, які можуть бути записані у вигляді 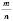 , де m – ціле число, n – натуральне.
, де m – ціле число, n – натуральне.
Кожне раціональне число можна подати у вигляді нескінченного періодичного десяткового дробу. І навпаки, кожний нескінченний періодичний десятковий дріб є раціональним числом.
Числа, які зображуються нескінченними неперіодичними десятковими дробами, називають ірраціональними.
Раціональні та ірраціональні числа утворюють Множину дійсних чисел.
множина натуральних чисел – N;
множина цілих чисел – Z;
множина раціональних чисел – Q;
множина дійсних чисел – R.
Зверніть увагу: кожне натуральне число є цілим, кожне ціле – раціональним, кожне раціональне – дійсним.
Приклади ірраціональних чисел:
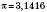 …; 0,12345…; 10,1010010001…;
…; 0,12345…; 10,1010010001…; 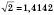 …
…Дійсні числа можна додавати, віднімати, множити, підносити до степеня й ділити (ділити – на числа, що відмінні від 0). Усі відомі властивості дій залишаються такими ж.
Related posts:
- ЦІЛІ ЧИСЛА. РАЦІОНАЛЬНІ ЧИСЛА Розділ 4 РАЦІОНАЛЬНІ ЧИСЛА ТА ДІЇ З НИМИ § 24. ЦІЛІ ЧИСЛА. РАЦІОНАЛЬНІ ЧИСЛА У п’ятому класі ви вивчали натуральні числа. Це числа, які використовують для лічби: 1; 2; 3; 4; … . Усі натуральні числа утворюють множину натуральних чисел. Цю множину позначають буквою N. Множина N має нескінченно багато елементів, оскільки натуральних чисел нескінченно […]...
- Раціональні числа, ірраціональні числа, дійсні числа, числові множини, етапи розвитку числа Урок № 37 Тема. Раціональні числа, ірраціональні числа, дійсні числа, числові множини, етапи розвитку числа Мета: систематизувати, узагальнити знання учнів щодо поняття числа та видів чисел, сформувати уявлення про множину дійсних чисел; сформувати вміння учнів відтворювати означення та властивості видів чисел, вивчених на уроці, виконувати найпростіші дії з дійсними числами (зокрема порівняння), використовувати вивчені властивості […]...
- Подільність цілих чисел Формули й таблиці МАТЕМАТИКА Подільність цілих чисел Ціле число а ділить ціле число b, або b ділиться на а, якщо існує таке ціле число с, при якому b = ас. Це має місце тоді, коли остача від ділення числа b на число а дорівнює нулю. Подільність цілих чисел має такі властивості: 1. Будь-яке ціле число […]...
- Цілі числа, раціональні числа Урок № 6 5 Тема. Цілі числа, раціональні числа Мета: узагальнити і систематизувати відомості учнів про види чисел; домогтися засвоєння поняття “ціле число”, “раціональне число” і зв’язок між ними; навчити класифікувати числа. Тип уроку: узагальнення і систематизація знань. Хід уроку І. Перевірка домашнього завдання (вибірково у “слабких” перевіряємо зошити) Математичний диктант Варіант 1 [2] 1. […]...
- Додатні та від’ємні числа Математика – Алгебра Раціональні числа Додатні та від’ємні числа Координатна пряма Пряма з вибраними на ній початком відліку, одиничним відрізком і вказаним додатним напрямом називається Координатною прямою. Число, що показує положення точки на координатній прямій, називається Координатою точки. Приклад Точка А розташована на прямій (див. рисунок) на відстані 2,5 одиничних відрізка праворуч від 0. Це […]...
- ДІЛЬНИКИ і КРАТНІ НАТУРАЛЬНОГО ЧИСЛА. ПРОСТІ ЧИСЛА Розділ 1 ПОДІЛЬНІСТЬ НАТУРАЛЬНИХ ЧИСЕЛ У розділі дізнаєтесь: – що таке дільники і кратні натурального числа; – які є ознаки подільності чисел; – які числа називаються простими та як їх знаходити; – як розкласти число на множники; – що таке найбільший спільний дільник чисел та як його знаходити; – що таке найменше спільне кратне чисел […]...
- Прості й складені числа Математика – Алгебра Подільність натуральних чисел Прості й складені числа Натуральне число називається Простим, якщо воно має тільки два різних дільники: одиницю й саме це число. Число, яке має більше двох дільників, називається складеним. Число 1 має єдиний дільник – 1, тому не належить ні до простих, ні до складених чисел. Приклади 1) Числа 2, […]...
- Протилежні числа. Цілі числа. Раціональні числа Розділ 4 Раціональні числа і дії мідними §35. Протилежні числа. Цілі числа. Раціональні числа Точки A і B з відповідними координатами 2 і -2 однаково віддалені від початку відліку – точки О і знаходять ся по різні боки від неї (мал. 71). Щоб потрапити з точки О в точки A(2) і B(-2), треба відкласти однакові […]...
- Дільники натурального числа. Прості і складені числа Урок № 1 Тема. Дільники Натурального Числа. Прості І Складені Числа Мета: систематизувати знання учнів про зміст дії ділення натуральних чисел; розширити знання учнів про властивості ділення натуральних чисел, доповнити їх уявленням про такі поняття, як дільник числа, кратне числу, прості і складені числа; сформувати вміння учнів знаходити дільник числа та класифікувати натуральні числа залежно […]...
- СПІВВІДНОШЕННЯ МІЖ РОЗРЯДНИМИ ОДИНИЦЯМИ. РОЗРЯДНИЙ СКЛАД ЧИСЛА НУМЕРАЦІЯ БАГАТОЦИФРОВИХ ЧИСЕЛ СПІВВІДНОШЕННЯ МІЖ РОЗРЯДНИМИ ОДИНИЦЯМИ. РОЗРЯДНИЙ СКЛАД ЧИСЛА 420. Розглянь таблицю. Прочитай числа. Запиши їх. Клас тисяч Клас одиниць Сотні тисяч Десятки тисяч Одиниці тисяч Сотні Десятки Одиниці 1 1 0 1 0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 0 0 Одиниці якого розряду містить […]...
- Натуральні числа і дії над ними Математика – Алгебра Натуральні числа і дії над ними Числа, які використовуються при лічбі предметів, називаються Натуральними числами. Натуральний ряд чисел є нескінченним. Він записується так: 1, 2, 3, … 0 не є натуральним числом. Зазвичай прийнято користуватись Позиційною десятковою системою числення. Тобто кожне число може бути записане за допомогою десяти цифр (0, 1, 2, […]...
- Раціональні числа: додавання і віднімання. Розв’язування вправ Урок № 79 Тема. Раціональні числа: додавання і віднімання. Розв’язування вправ Мета: підготувати учнів до виконати тематичної контрольної роботи. Тип уроку: узагальнення та систематизації знань, вдосконалення вмінь. Хід уроку І. Перевірка домашнього завдання @ Оскільки вправи домашнього завдання дублюють вправи, розв’язані на попередньому уроці, доцільно з метою збереження часу, перевірити вибірково зошити у “слабких” учнів […]...
- Дільники і кратні Математика – Алгебра Подільність натуральних чисел Дільники і кратні Дільником натурального числа а називають натуральне число, на яке а ділиться без остачі. Кратним натуральному числу а називається натуральне число, яке ділиться на а без остачі. Приклади 1) Число 12 має 6 дільників: 1, 2, 3, 4, 6, 12. (Зверніть увагу: .) 2) Запишемо п’ять перших […]...
- Ділення раціональних чисел Математика – Алгебра Раціональні числа Ділення раціональних чисел Часткою двох від’ємних чисел є число додатне. Щоб знайти його модуль, треба модуль діленого поділити на модуль дільника. Часткою двох чисел із різними знаками є число від’ємне. Щоб знайти його модуль, треба модуль діленого поділити на модуль дільника. Для будь-якого числа а: ; ; Для : ; […]...
- ДІЛЕННЯ РАЦІОНАЛЬНИХ ЧИСЕЛ Розділ 4 РАЦІОНАЛЬНІ ЧИСЛА ТА ДІЇ З НИМИ § 29. ДІЛЕННЯ РАЦІОНАЛЬНИХ ЧИСЕЛ Ви знаєте, що для додатних чисел дію ділення можна звести до дії множення на число, обернене до дільника. Нехай треба поділити число 20 на число Це означає, що число 20 можна помножити на число, обернене до числа тобто на число Тоді, за […]...
- МАТЕМАТИКА Формули й таблиці МАТЕМАТИКА Натуральні числа Натуральні – числа 1, 2, 3, що використовуються для рахунку предметів. Позначається буквою N. Просте число – натуральне число, що має тільки 2 дільники: самого себе й одиницю. Таких чисел нескінченна множина. Якщо число n – це добуток двох чисел: n = m · k, то воно ділиться без […]...
- Модуль числа Математика – Алгебра Раціональні числа Модуль числа Відстань від початку відліку до точки, що зображає число на координатній прямій, називається Модулем даного числа. Позначення: – модуль а. Очевидно, що для додатних чисел і 0 , для від’ємних . для будь-якого числа а. Модулі протилежних чисел рівні: . Приклади 1) ; ; . 2) Розв’яжіть рівняння. […]...
- Розкладання числа на прості множники Математика – Алгебра Подільність натуральних чисел Розкладання числа на прості множники Розкласти число на прості множники означає записати його у вигляді добутку простих чисел. Наприклад, . Кожне складене число можна розкласти на прості множники єдиним способом (якщо не враховувати порядок множників). Розкладання зручно робити за такою схемою. Наприклад, візьмемо число 2100. Запишемо число 2100 і […]...
- ЧИСЛО 10. ПОНЯТТЯ “ДЕСЯТИЙ”. ДОПОВНЕННЯ ДО 10. УТВОРЕННЯ ЧИСЛА 10. НАТУРАЛЬНІ ЧИСЛА ОЗНАКИ І ВЛАСТИВОСТІ ПРЕДМЕТІВ. МНОЖИНИ. ГЕОМЕТРИЧНІ ФІГУРИ. НАТУРАЛЬНІ ЧИСЛА 1-10 І ЧИСЛО 0 Урок 36. ЧИСЛО 10. ПОНЯТТЯ “ДЕСЯТИЙ”. ДОПОВНЕННЯ ДО 10. УТВОРЕННЯ ЧИСЛА 10. НАТУРАЛЬНІ ЧИСЛА Мета: ввести поняття “десятий”; ознайомити учнів з утворенням числа 10 і написанням числа за допомогою цифр 1 і 0; учити порівнювати предмети, доповнювати до 10; закріплювати вміння співвідносити […]...
- Множення числа на добуток. Усний і письмовий способи множення на розрядні числа (№№ 92-101) Тема. Множення числа на добуток. Усний і письмовий способи множення на розрядні числа (№№ 92-101). Мета. Систематизувати знання учнів про множення числа на добуток; вдосконалювати обчислювальні навички; формувати вміння множити на розрядні числа різними способами, добирати числові дані та розв’язувати складені задачі вивчених типів; знаходити значення буквених виразів; розвивати вміння аналізувати, робити висновки. Обладнання. Таблиці […]...
- Прості та складені числа Розділ 1 Подільність натуральних чисел §4. Прості та складені числа Число 11 ділиться тільки на 1 і на себе. Іншими словами, число 11 має тільки два дільники: 1 і 11. У числа 8 чотири дільники: 1, 2, 4 і 8. Число 18 має шість дільників: 1, 2, 3, 6, 9 і 18. Такі числа, як […]...
- Взаємно обернені числа Розділ 2 Звичайні дроби §16. Взаємно обернені числа Розглянемо дріб і поміняємо в ньому чисельник і знаменник місцями. Отримаємо дріб Якщо тепер помножити дріб то отримаємо 1: Також отримаємо 1 при множенні 5 на тощо. – Два числа, добуток яких дорівнює 1, називають взаємно оберненими. Легко зробити висновок: щоб знайти дріб взаємно обернений з даним […]...
- ЧИСЛА І ЦИФРИ. ОДНОЦИФРОВІ ЧИСЛА. СКЛАДАННЯ ПРИКЛАДІВ ЗА ЧИСЛОВИМИ ПРОМЕНЯМИ. ПОРІВНЯННЯ ЧИСЕЛ ОЗНАКИ І ВЛАСТИВОСТІ ПРЕДМЕТІВ. МНОЖИНИ. ГЕОМЕТРИЧНІ ФІГУРИ. НАТУРАЛЬНІ ЧИСЛА 1-10 І ЧИСЛО 0 Урок 34. ЧИСЛА І ЦИФРИ. ОДНОЦИФРОВІ ЧИСЛА. СКЛАДАННЯ ПРИКЛАДІВ ЗА ЧИСЛОВИМИ ПРОМЕНЯМИ. ПОРІВНЯННЯ ЧИСЕЛ Мета: ознайомити учнів з поняттям “одноцифрові числа”; узагальнити поняття “число” і “цифра”; учити порівнювати числа, складати приклади за числовими променями; розвивати мислення; виховувати інтерес до математики. Хід уроку […]...
- Додавання на основі розрядного складу числа Додавання на основі розрядного складу числа Сума розрядних доданків 1 Назви числа: більші за 5 489, але менші від 5 512; більші за 34 987, але менші від 35 020; більші за 267 178, але менші від 267 207. 2 Запиши числа. Розбий отриману множину на підмножини. Прочитай елементи кожної підмножини. Допиши до кожної підмножини […]...
- Дільники і кратні натурального числа Розділ 1 Подільність натуральних чисел У цьому розділі ви: – ознайомитеся з дільниками і кратними натуральних чисел; – дізнаєтеся про прості та складені числа, взаємно прості числа; – навчитеся розкладати числа на прості множники, знаходити найбільший спільний дільник і найменше спільне кратне натуральних чисел. §1. Дільники і кратні натурального числа 15 яблук можна розділити порівну […]...
- Раціональні числа; порівняння, додавання та віднімання. Розв’язування вправ Урок № 7 8 Тема. Раціональні числа; порівняння, додавання Та віднімання. Розв’язування вправ Мета: підготувати учнів до виконання тематичної контрольної роботи. Тип уроку: узагальнення та систематизація знань, умінь і навичок. Хід уроку I. Перевірка домашнього завдання @ Якщо на попередньому уроці не встигли зробити, то на початку цього уроку ми проводимо тестову роботу (з теми […]...
- Стандартний вигляд числа Урок № 28 Тема. Стандартний вигляд числа Мета: засвоєння учнями змісту алгоритмів виконання дій множення та ділення чисел, записаних у стандартному вигляді; формування вмінь учнів застосовувати вивчені алгоритми для виконання названих дій із числами, записаними у стандартному вигляді під час розв’язування фізичних та геометричних задач. Тип уроку: засвоєння знань та вмінь. Наочність та обладнання: опорний […]...
- Застосування модуля числа. Відстань між точками на координатній прямій Урок № 6 7 Тема. Застосування модуля числа. Відстань між точками на координатній прямій Мета: поглибити знання учнів про властивості модуля раціонального числа та відпрацювати навички застосування означення та властивостей модуля для розв’язування рівнянь та нерівностей. Тип уроку: застосування знань, умінь і навичок Хід уроку I. Перевірка домашнього завдання Математичний диктант Варіант 1 [2] 1. […]...
- Натуральні числа. Натуральний ряд чисел. Десяткова система числення Нумерація чисел у межах мільйона Натуральні числа. Натуральний ряд чисел. Десяткова система числення Числа, які використовують під час лічби, називають натуральними. Якщо натуральні числа розмістити так, щоб кожне наступне число було на 1 більше за попереднє, то дістанемо натуральний ряд чисел: 1, 2, З,4, 5 ,6 ,7 ,8 , 9, 10,11,12, 13, 14, 15,… Найменше […]...
- Знаходження дробу від числа ст.99 Знаходження дробу від числа 1 Знайди дріб від числа. від 72; від 88; від 48. 2 Зістав задачі 1 і 2. Що в них спільне? відмінне? Розв’яжи задачу 1. Розв’яжи задачу 2. Запиши розв’язання задачі 2 по діях і виразом. Прочитай одержаний вираз і поясни, що позначає кожне числе Спробуй сформулювати, використавши слова “чи сельник” […]...