Головна ⇒ 📌Довідник с фізики ⇒ Динаміка спеціальної теорії відносності

Динаміка спеціальної теорії відносності

ФІЗИКА

Частина 4

ОПТИКА. СПЕЦІАЛЬНА ТЕОРІЯ ВІДНОСНОСТІ

Розділ 14 ШВИДКІСТЬ ПОШИРЕННЯ СВІТЛА. ОСНОВИ СПЕЦІАЛЬНОЇ ТЕОРІЇ ВІДНОСНОСТІ

14.8. Динаміка спеціальної теорії відносності

Ми розглянули винятково просторово-часові співвідношення, кінематику теорії відносності. Тепер ознайомимося з релятивістською динамікою.

Мірою взаємодії одного тіла з іншим є сила. Маса тіла вводиться як індивідуальна стала характеристика, що вимірюється інертністю тіла. Важливим етапом у розвитку механіки стало введення більш абстрактних

понять: імпульсу (

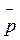= m

) і кінетичної енергії тіла (Е = mυ2 /2).

Імпульс і кінетична енергія – дві різні міри руху. Кінетична енергія як величина скалярна характеризує рух тільки з кількісного боку, імпульс як величина векторна показує ще й напрям руху. Класична динаміка грунтується на другому законі Ньютона, який стверджує, що зміна імпульсу пропорційна діючій силі й відбувається у напрямі дії сили:

До того ж, як стверджує дослід, перехід від системи К до системи К’, що рухається відносно системи К зі сталою швидкістю и у напрямі осі

х (див. рис. 14.5), супроводжується зміною компонентів сили за такими формулами:

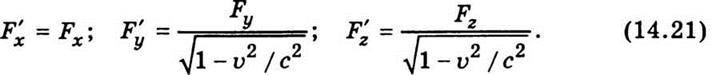
Незбереження сили при переході від однієї інерціальної системи до іншої зумовлене тим, що довжини відрізків у напрямі руху і проміжки часу, від яких залежать сили, змінюються.

А. Ейнштейн довів, що другий закон Ньютона (14.20) інваріантний перетворенням Лоренца, якщо імпульс тіла в інерціальній системі відліку визначити так:

Де m – маса тіла; – швидкість тіла в обраній системі відліку; с – швидкість світла у вакуумі.

Отже, в релятивістській динаміці, як і в ньютонівській, імпульс матеріальної точки пропорційний її масі m і збігається за напрямом зі швидкістю цієї точки. Проте на відміну від ньютонівської динаміки імпульс матеріальної точки є нелінійною функцією її швидкості.

При цьому прийнято вважати, що маса m не залежить від швидкості матеріальної точки і тим самим є інваріантною відносно вибору систем відліку. Якщо υ ” с, то вираз (14.22) практично дорівнює ти, тобто збігається зі значенням імпульсу матеріальної точки в ньютонівській механіці. Імпульс 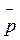, виражений формулою (14.22), інколи називають релятивістським імпульсом матеріальної точки*.

Таким чином, в релятивістській області між імпульсом тіла і швидкістю вже немає пропорційної залежності, а існує більш складна залежність, яка виражається формулою (14.22).

Другий закон Ньютона в релятивістській формі має такий вигляд:

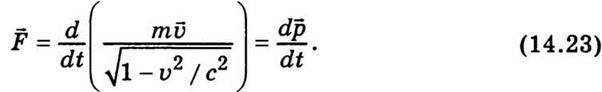
Із (14.22) видно, що 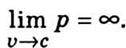Усі реальні сили скінченні, а їх дія на тіло обмежена за часом. Тому відповідно до (14.23) вони не можуть надати тілу нескінченно великий імпульс. Отже, швидкість тіла відносно будь-якої інерціальної системи відліку не може дорівнювати швидкості світла у вакуумі, а є меншою від неї.

Це твердження справедливе для атомів, молекул і всіх елементарних частинок, за винятком фотонів, нейтрино і антинейтрино, маса яких дорівнює нулю**, тому їх швидкість не може відрізнятися від швидкості світла у вакуумі.

На відміну від ньютонівської механіки сила 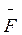, яка діє на матеріальну точку, не інваріантна відносно вибору інерціальної системи відліку. Правила перетворення компонент сили при переході від однієї інерціальної системи відліку до іншої можна отримати із умови ло – ренц-інваріантності рівняння (14.23). При малих швидкостях (υ ” с) рівняння (14.23) практично збігається з основним рівнянням ньютонівської динаміки (2.7). Проте зі збільшенням швидкості матеріальної точки її імпульс зростає швидше, ніж змінюється швидкість.

_____________________________________________________________

*Донедавна масу m звичайно називали масою спокою матеріальної точки, а 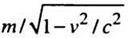– релятивістською масою цієї точки. Відповідно вважали, що маса матеріальної точки залежить від її швидкості.