Головна ⇒ 📌Математика ⇒ Додавання і віднімання десяткових дробів

Додавання і віднімання десяткових дробів

Розділ 2 ДРОБОВІ ЧИСЛА І Дії З НИМИ

§ 37. Додавання і віднімання десяткових дробів

Десяткові дроби записують за тим самим принципом, що й натуральні числа. Тому додавання і віднімання виконують за відповідними схемами для натуральних чисел.

Під час додавання і віднімання десяткові дроби записують “стовпчиком” – один під одним так, щоб однойменні розряди стояли один під одним. Таким чином, кома буде стояти під комою. Далі виконуємо дію так, як і з натуральними числами, не звертаючи уваги на коми. У сумі (або різниці) кому ставимо

під комами доданків (або комами зменшуваного і від’ємника).

Приклад 1. 37,982 + 4,473.

Пояснення. 2 тисячних плюс 3 тисячних дорівнює 5 тисячних. 8 сотих плюс 7 сотих дорівнює 15 сотих, або 1 десята і 5 сотих. Записуємо 5 сотих, а 1 десяту запам’ятовуємо і т. д.

Приклад 2. 42,8 – 37,515.

Пояснення. Оскільки зменшуване і від’ємник мають різну кількість знаків після коми, то можна приписати в зменшуваному необхідну кількість нулів. Розберися самостійно, як виконано приклад.

Додавання і віднімання десяткових дробів

Додавання і віднімання десяткових дробів

Зауважимо, що при додаванні та відніманні нулі можна й не дописувати, а подумки

уявляти їх на тих місцях, де немає розрядних одиниць.

При додаванні десяткових дробів справджуються вивчені раніше переставна і сполучна властивості додавання:

Додавання і віднімання десяткових дробів

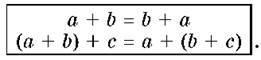
Початковий рівень

1228. Обчисли (усно):

1) 8 + 0,7; 2) 5 + 0,32;

3) 0,39 + 1; 4) 0,3 + 0,2;

5) 0,12 + 0,37; 6) 0,1 + 0,01;

7) 0,02 + 0,003; 8) 0,26 + 0,7;

9) 0,12 + 0,004.

1229. Обчисли:

Додавання і віднімання десяткових дробів

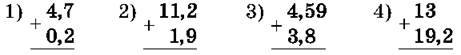
1230. Обчисли (усно):

1) 4,72 – 2; 2) 13,892 – 10; 3) 0,8 – 0,6;

4) 6,7 – 0,3; 5) 2,3 – 1,2; 6) 0,05 – 0,02;

7) 0,19 – 0,07; 8) 0,47 – 0,32; 9) 42,4 – 42.

1231. Обчисли:

Додавання і віднімання десяткових дробів

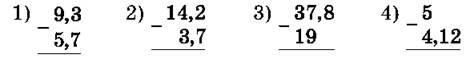
1232. Обчисли:

Додавання і віднімання десяткових дробів

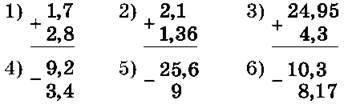
1233. На одній машині було 2,7 т піску, а на іншій – 3,2 т. Скільки піску було на двох машинах?

1234. Виконай додавання:

1) 6,9 + 2,6; 2) 9,3 + 0,8; 3) 8,9 + 5;

4) 15 + 7,2; 5) 4,7 + 5,29; 6) 1,42 + 24,5;

7) 10,9 + 0,309; 8) 0,592 + 0,83; 9) 1,723 + 8,9.

1235. Знайди суму:

1) 3,8 + 1,9; 2) 5,6 + 0,5; 3) 9 + 3,6;

4) 5,7 + 1,6; 5) 3,58 + 1,4; 6) 7,2 + 15,68;

7) 0,906 + 12,8; 8) 0,47 + 0,741; 9) 8,492 + 0,7.

1236. Виконай віднімання:

1) 5,7 – 3,8; 2) 6,1 – 4,7; 3) 12,1 – 8,7;

4) 44,6 – 13; 5) 4 – 3,4; 6) 17 – 0,42;

7) 7,5 – 4,83; 8) 0,12 – 0,0856; 9) 9,378 – 8,45.

1237. Знайди різницю:

1) 7,5 – 2,7; 2) 4,3 – 3,5; 3) 12,2 – 9,6;

4) 32,7 – 5; 5) 41 – 3,53; 6) 7 – 0,61;

7) 8,31 – 4,568; 8) 0,16 – 0,0913; 9) 37,819 – 8,9.

1238. Килим-літак за 2 год пролетів 17,4 км, причому за першу годину він пролетів 8,3 км. Скільки пролетів килим-літак за другу годину?

1239. 1) Збільши число 7,2831 на 2,423.

2) Зменши число 5,372 на 4,47.

Середній рівень

1240. Розв’яжи рівняння:

1) 7,2 + х = 10,31; 2) 5,3 – х = 2,4;

3) х – 2,8 = 1,72; 4) х + 3,71 = 10,5.

1241. Розв’яжи рівняння:

1) х – 4,2 = 5,9; 2) 2,9 + х = 3,5;

3) 4,13 – х = 3,2; 4) х + 5,72 = 14,6.

1242. Як зручніше додати? Чому?

4,2 + 8,93 + 0,8 = (4,2 + 8,93) + 0,8 чи

4,2 + 8,93 + 0,8 = (4,2 + 0,8) + 8,93.

1243. Обчисли (усно) найзручнішим способом:

1) 7 + 2,8 + 1,2; 2) 12,4 + 17,3 + 0,6;

3) 3,42 + 4,9 + 5,1; 4) 12,11 + 7,89 + 13,5.

1244. Знайди значення виразу:

1) 200,01 + 0,052 + 1,05;

2) 42 + 4,038 + 17,25;

3) 2,546 + 0,597 + 82,04;

4) 48,086 + 115,92 + 111,037.

1245. Знайди значення виразу:

1) 82 + 4,042 + 17,37;

2) 47,82 + 0,382 + 17,3;

3) 15,397 + 9,42 + 114;

4) 152,73 + 137,8 + 0,4953.

1246. Від металевої труби завдовжки 7,92 м відрізали спочатку 1,17 м, а потім ще 3,42 м. Яка довжина решти труби?

1247. Яблука разом з ящиком важать 25,6 кг. Скільки кілограмів важать яблука, якщо порожній ящик важить 1,13 кг?

1248. Знайди довжину ламаної ABC, якщо АВ = 4,7 см, а ВС на 2,3 см менше від АВ.

1249. В одному бідоні є 10,7 л молока, а в іншому – на 1,25 л менше. Скільки молока у двох бідонах?

1250.Обчисли:

1) 147,85 – 34 – 5,986;

2) 137,52 – (113,21 + 5,4);

3) (157,42 – 114,381) – 5,91;

4) 1142,3 – (157,8 – 3,71).

1251. Обчисли:

1) 137,42 – 15 – 9,127;

2) 1147,58 – (142,37 + 8,13);

3) (159,52 – 142,78) + 11,189;

4) 4297,52 – (113,43 + 1298,3).

1252. Знайди значення виразу а – 5,2 – b, якщо а = 8,91, b = 0,13.

1253. Швидкість човна в стоячій воді 17,2 км/год, а швидкість течії 2,7 км/год. Знайди швидкість човна за течією і проти течії.

1254. Заповни таблицю:

Власна

Швидкість,

Км/год

Швидкість

Течії,

Км/год

Швидкість за течією, км/год

Швидкість проти течії, км/год

13,1

1,8

17,2

18,5

12,35

10,85

2,1

13,5

1,65

12,95

1255. Знайди пропущені числа в ланцюжку:

Додавання і віднімання десяткових дробів

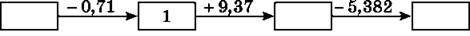
1256. Виміряй у сантиметрах сторони чотирикутника, зображеного на рисунку 257, та знайди його периметр.

1257. Накресли довільний трикутник, виміряй його сторони в сантиметрах та знайди периметр трикутника.

1258. На відрізку АС позначили точку В (рис. 258).

1) Знайди АС, якщо АВ = 3,2 см, ВС = 2,1 см;

2) знайди ВС, якщо АС = 12,7 дм, АВ = 8,3 дм.

Додавання і віднімання десяткових дробів

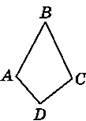
Рис. 257

Додавання і віднімання десяткових дробів

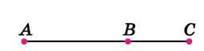
Рис. 258

Додавання і віднімання десяткових дробів

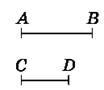
Рис. 259

1259. На скільки сантиметрів відрізок AB довший за відрізок CD (рис. 259)?

1260. Одна сторона прямокутника дорівнює 2,7 см, а інша – на 1,3 см коротша. Знайди периметр прямокутника.

1261. Основа рівнобедреного трикутника дорівнює 8,2 см, а бічна сторона на 2,1 см менша від основи. Знайди периметр трикутника.

1262. Перша сторона трикутника дорівнює 13,6 см, друга на 1,3 см коротша від першої. Знайди третю сторону трикутника, якщо його периметр дорівнює 43,1 см.

Достатній рівень

1263. Запиши послідовність з п’яти чисел, якщо:

1) перше число дорівнює 7,2, а кожне наступне на 0,25 більше за попереднє;

2) перше число дорівнює 10,18, а кожне наступне на 0,34 менше від попереднього.

1264. У першому ящику було 12,7 кг яблук, що на 3,9 кг більше, ніж у другому. У третьому ящику яблук було на 5,13 кг менше, ніж у першому і другому разом. Скільки кілограмів яблук було в трьох ящиках разом?

1265. Першого дня туристи пройшли 8,3 км, що на 1,8 км більше, ніж другого дня, і на 2,7 км менше, ніж третього. Скільки кілометрів пройшли туристи за три дні?

1266. Виконай додавання, обираючи зручний порядок обчислення:

1) 0,571 + (2,87 + 1,429);

2) 6,335 + 2,896 + 1,104;

3) 4,52 + 3,1 + 17,48 + 13,9.

1267. Виконай додавання, обираючи зручний порядок обчислення:

1) 0,571 + (2,87 + 1,429);

2) 7,335 + 3,896 + 1,104;

3) 15,2 + 3,71 + 7,8 + 4,29.

1268. Постав замість зірочок цифри:

Додавання і віднімання десяткових дробів

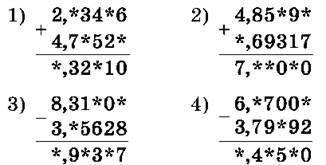
1269. Постав у клітинки такі цифри, щоб утворилися правильно виконані приклади:

Додавання і віднімання десяткових дробів

1270. Спрости вираз:

1) 2,71 + х – 1,38; 2) 3,71 + с + 2,98.

1271. Спрости вираз:

1) 8,42 + 3,17 – х; 2) 3,47 + y – 1,72.

1272. Знайди закономірність і запиши три наступ них числа послідовності:

1) 2; 2,7; 3,4 … 2) 15; 13,5; 12 …

1273. Розв’яжи рівняння:

1) 13,1 – (x + 5,8) = 1,7;

2) (х – 4,7) – 2,8 = 5,9;

3) (у – 4,42) + 7,18 = 24,3;

4) 5,42 – (у – 9,37) = 1,18.

1274. Розв’яжи рівняння:

1) (3,9 + х) – 2,5 = 5,7;

2) 14,2 – (6,7 + х) = 5,9;

3) (у – 8,42) + 3,14 = 5,9;

4) 4,42 + (у – 1,17) = 5,47.

1275. Знайди значення виразу зручним способом, використовуючи властивості віднімання:

1) (14,548 + 12,835) – 4,548;

2) 9,37 – 2,59 – 2,37;

3) 7,132 – (1,132 + 5,13);

4) 12,7 – 3,8 – 6,2.

1276. Знайди значення виразу зручним способом, використовуючи властивості віднімання:

1) (27,527 + 7,983) – 7,527;

2) 14,49 – 3,1 – 5,49;

3) 14,1 – 3,58 – 4,42;

4) 4,142 – (2,142 + 1,9).

1277. Обчисли, записавши дані величини в дециметрах:

1) 8,72 дм – 13 см;

2) 15,3 дм + 5 см + 2 мм;

3) 427 см + 15,3 дм;

4) 5 м 3 дм 2 см – 4 м 7 дм 2 см.

1278. Периметр рівнобедреного трикутника дорівнює

17,1 см, а бічна сторона – 6,3 см. Знайди довжину основи.

1279. Швидкість товарного потяга 52,4 км/год, пасажирського 69,5 км/год. Визнач, віддаляються чи зближуються ці потяги і на скільки кілометрів за годину, якщо вони вийшли одночасно:

1) з двох пунктів, відстань між якими 600 км, назустріч один одному;

2) з двох пунктів, відстань між якими 300 км, і пасажирський наздоганяє товарний;

3) з одного пункту в протилежних напрямах;

4) з одного пункту в одному напрямі.

1280. Швидкість першого велосипедиста 18,2 км/год, а другого 16,7 км/год. Визнач, віддаляються чи зближаються велосипедисти і на скільки кілометрів за годину, якщо вони виїхали одночасно:

1) з двох пунктів, відстань між якими 100 км, назустріч один одному;

2) з двох пунктів, відстань між якими 30 км, і перший наздоганяє другого;

3) з одного пункту в протилежних напрямах;

4) з одного пункту в одному напрямі.

1281. Обчисли, відповідь округли до сотих:

1) 1,5972 + 7,8219 – 4,3712;

2) 2,3917 – 0,4214 + 3,4515.

1282. Обчисли, записавши дані величини в центнерах:

1) 8 ц – 319 кг;

2) 9 ц 15 кг + 312 кг;

3) 3 т 2 ц – 2 ц 3 кг;

4) 5 т 2 ц 13 кг + 7 т 3 ц 7 кг.

1283. Обчисли, записавши дані величини в метрах:

1) 7,2 м – 25 дм;

2) 2,7 м + 3 дм 5 см;

3) 432 дм + 3 м 5 дм + 27 см;

4) 37 дм – 15 см.

1284. Периметр рівнобедреного трикутника дорівнює

15,4 см, а основа – 3,4 см. Знайди довжину бічної сторони.

1285. Периметр прямокутника дорівнює 12,2 см, а довжина однієї зі сторін – 3,1 см. Знайди довжину сторони, що не дорівнює даній.

1286. У трьох ящиках 109,6 кг помідорів. У першому і другому ящиках разом 69,9 кг, а в другому і третьому 72,1 кг. Скільки кілограмів помідорів у кожному ящику?

1287. Знайди числа a, b, с, d у ланцюжку:

Додавання і віднімання десяткових дробів

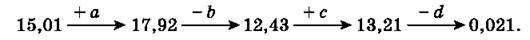
1288. Знайди числа а і b у ланцюжку:

Додавання і віднімання десяткових дробів

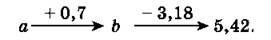
Високий рівень

1289. Постав замість зірочок знаки “+” і “-” так, щоб виконувалася рівність:

1) 8,1 * 3,7 * 2,7 * 5,1 = 2;

2) 4,5 * 0,18 * 1,18 * 5,5 = 0.

1290. У Чіпа було 5,2 грн. Після того як Дейл позичив йому 1,7 грн., у Дейла стало на 1,2 грн. менше, ніж у Чіпа. Скільки грошей було в Дейла спочатку?

1291. Дві бригади асфальтують шосе і рухаються одна одній назустріч. Коли перша бригада заасфальтувала 5,92 км шосе, а друга – на 1,37 км менше, то до їхньої зустрічі залишилося 0,85 км. Яка довжина ділянки шосе, яку необхідно було заасфальтувати?

1292. Як зміниться сума двох чисел, якщо:

1) один з доданків збільшити на 3,7, а інший – на 8,2;

2) один з доданків збільшити на 18,2, а інший зменшити на 3,1;

3) один з доданків зменшити на 7,4, а інший – на 8,15;

4) один з доданків збільшити на 1,25, а інший зменшити на 1,25;

5) один з доданків збільшити на 7,2, а інший зменшити на 8,9?

1293. Як зміниться різниця, якщо:

1) зменшуване зменшити на 7,1;

2) зменшуване збільшити на 8,3;

3) від’ємник збільшити на 4,7;

4) від’ємник зменшити на 4,19?

1294. Різниця двох чисел дорівнює 8,325. Чому дорівнює нова різниця, якщо зменшуване збільшити на 13,2, а від’ємник збільшити на 5,7?

1295. Як зміниться різниця, якщо:

1) збільшити зменшуване на 0,8, а від’ємник – на 0,5;

2) збільшити зменшуване на 1,7, а від’ємник – на 1,9;

3) зменшуване збільшити на 3,1, а від’ємник зменшити на 1,9;

4) зменшуване зменшити на 4,2, а від’ємник збільшити на 2,1?

Вправи для повторення

1296. Порівняй значення виразів, не виконуючи дій:

1) 125 + 382 і 382 + 127; 2) 473 ∙ 29 і 472 ∙ 29;

3) 592 – 11 і 592 – 37; 4) 925 : 25 і 925 : 37.

1297. У їдальні є два види перших страв, 3 види других та 2 види третіх страв. Скількома способами можна вибрати обід з трьох страв у цій їдальні?

1298. Периметр прямокутника дорівнює 50 дм. Довжина прямокутника на 5 дм більша за ширину. Знайди сторони прямокутника.

1299. Запиши найбільший десятковий дріб:

1) з одним десятковим знаком, менший від 10;

2) з двома десятковими знаками, менший від 5.

1300. Запиши найменший десятковий дріб:

1) з одним десятковим знаком, більший за 6;

2) з двома десятковими знаками, більший за 17.

Домашня самостійна робота № 7

Додавання і віднімання десяткових дробів

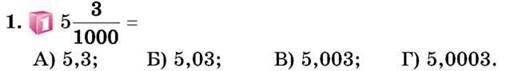
2. Яка з нерівностей правильна:

A) 2,3 > 2,31; Б) 7,5 < 7,49;

B) 4,12 > 4,13; Г) 5,7 < 5,78?

3. 4,08 – 1,3 =

А) 3,5; Б) 2,78; В) 3,05; Г) 3,95.

4. Запиши десятковий дріб 4,0701 мішаним числом:

Додавання і віднімання десяткових дробів

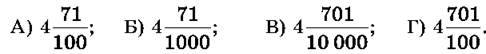
5. Яке з округлень до сотих виконано правильно:

A) 2,729 ≈ 2,72; Б) 3,545 ≈ 3,55;

B) 4,729 ≈ 4,7; Г) 4,365 ≈ 4,36?

6. Знайди корінь рівняння х – 6,13 = 7,48.

А) 13,61; Б) 1,35; В) 13,51; Г) 12,61.

7. Яка із запропонованих рівностей правильна:

А) 7 см = 0,7 м; Б) 7 дм2 = 0,07 м2;

В) 7 мм = 0,07 м; Г) 7 см3 = 0,07 м3?

8. Назви найбільше натуральне число, що не перевищує 7,0809:

А) 6; Б) 7; В) 8; Г) 9.

9. Скільки існує цифр, що можна поставити замість зірочки у наближеній рівності 2,3*7 * 2,4, щоб округлення до дестих було виконано правильно?

А) 5; Б) 0; В) 4; Г) 6.

10. 4 а 3 м2 =

А) 4,3 а; Б) 4,003 а; В) 4,03 а; Г) 43 а.

11. Яке із запропонованих чисел можна підставити замість а, щоб подвійна нерівність 3,7 < а < 3,9 була правильною?

А) 3,08; Б) 3,901; В) 3,699; Г) 3,83.

12. Як зміниться сума трьох чисел, якщо перший доданок збільшити на 0,8, другий – збільшити на 0,5, а третій – зменшити на 0,4?

A) збільшиться на 1,7; Б) збільшиться на 0,9;

B) збільшиться на 0,1; Г) зменшиться на 0,2.

Завдання для перевірки знань № 7 (§34 – §37)

1. Порівняй десяткові дроби:

1) 47,539 і 47,6; 2) 0,293 і 0,2928.

2. Виконай додавання:

1) 7,97 + 36,461; 2) 42 + 7,001.

3. Виконай віднімання:

1) 46,63 – 7,718; 2) 37 – 3,045.

4. Округли до:

1) десятих: 4,597; 0,8342;

2) сотих: 15,795; 14,134.

5. Вирази в кілометрах і запиши десятковим дробом:

1) 7 км 113 м; 2) 219 м; 3) 17 м; 4) 3129 м.

6. Власна швидкість човна дорівнює 15,7 км/год, а швидкість течії – 1,9 км/год. Знайди швидкість човна за течією і проти течії.

7. Першого дня на склад завезли 7,3 т овочів, що на 2,6 т більше, ніж другого, і на 1,7 т менше, ніж третього дня. Скільки тонн овочів завезли на склад за три дні?

8. Знайди значення виразу, обираючи зручний порядок дій:

1) (8,42 + 3,97) + 4,58; 2) (3,47 + 2,93) – 1,47.

9. Запиши три числа, кожне з яких менше від 5,7, але більше за 5,5.

10. Додаткове завдання. Запиши всі цифри, які можна поставити замість *, щоб правильною була наближена нерівність:

1) 3,81*5 ≈3,82; 2) 7,4*6≈ 7,41.

11. Додаткове завдання. При яких натуральних значеннях n нерівності 0,7 < n < 4,2 і 2,7 < n < 8,9 одночасно є правильними?


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Додавання і віднімання десяткових дробів УРОК 92 Тема. Додавання і віднімання десяткових дробів Мета: узагальнити досвід учнів, набутий під час вивчення теми “Додавання і віднімання десяткових дробів”; перевірити ступінь засвоєння знань, умінь учнів з теми. Тип уроку: перевірка та корекція знань, навичок та вмінь Хід уроку І. Відтворення знань Усні вправи 1. Знайдіть числа, яких не вистачає в ланцюжку обчислень: […]...

  2. Поняття про десятковий дріб. Порівняння, округлення, додавання і віднімання десяткових дробів УРОК 94 Тема. Поняття про десятковий дріб. Порівняння, округлення, додавання і віднімання десяткових дробів Мета: перевірити рівень навчальних досягнень учнів з теми. Тип уроку: перевірка й корекція знань, навичок і вмінь. Хід уроку І. Умова тематичної контрольної роботи Варіант 1 1°. Порівняйте: 1) 18, 3 і 18,287; 2) 0,5438 і 0,544. 2°. Округліть 1) до […]...

  3. Додавання і віднімання дробів з різними знаменниками Розділ 2 Звичайні дроби §10. Додавання і віднімання дробів з різними знаменниками Ми вже вміємо додавати і віднімати дроби з однаковими знаменниками: Щоб додати (відняти) дроби з різними знаменниками, достатньо: 1) звести ці дроби до найменшого спільного знаменника; 2) додати (відняти) їх за правилом додавання (віднімання) дробів з однаковими знаменниками. Приклад 1. Знайти суму Розв’язання. […]...

  4. Додавання і віднімання звичайних дробів з однаковими знаменниками Розділ 2 ДРОБОВІ ЧИСЛА І Дії З НИМИ § 32. Додавання і віднімання звичайних дробів з однаковими знаменниками Зі звичайними дробами, так само, як і з натуральними числами, можна виконувати арифметичні дії. Розглянемо додавання і віднімання дробів з однаковими знаменниками. На рисунку 244 зображено додавання відрізків OA і АВ: OA + АВ = ОВ. Довжина […]...

  5. Розв’язування рівнянь та задач на додавання і віднімання десяткових дробів Урок № 20 Тема. Розв’язування рівнянь та задач на додавання і віднімання десяткових дробів Мета уроку. Вироблення навичок та вмінь розв’язувати задачі та рівняння. Тип уроку. Узагальнення і систематизація знань. Хід уроку І. Письмова перевірка домашнього завдання № 1175, 1709, 1220, 1227. ІІ. Розв’язування задач Колективне розв’язування № 1213, 1214, з коментуванням. Напівсамостійне розв’язування рівнянь. […]...

  6. Множення десяткових дробів Розділ 2 ДРОБОВІ ЧИСЛА І Дії З НИМИ § 38. Множення десяткових дробів Щоб виконувати множення десяткових дробів, треба вміти множити натуральні числа і навчитися правильно визначати місце коми в отриманому добутку. Розглянемо приклад, який допоможе сформулювати правило множення десяткових дробів. Задача 1. Сторони прямокутника 3,7 дм і 4,5 дм. Знайди його площу. Розв’язання. Оскільки […]...

  7. ДОДАВАННЯ ТА ВІДНІМАННЯ ДРОБІВ З ОДНАКОВИМИ ЗНАМЕННИКАМИ ЗАДАЧІ НА ПОВТОРЕННЯ ДОДАВАННЯ ТА ВІДНІМАННЯ ДРОБІВ З ОДНАКОВИМИ ЗНАМЕННИКАМИ 85. Обчисліть: 86. Заповніть клітинки квадратів так, щоб суми чисел у кожному рядку, стовпці і діагоналі були рівними між собою. 87. Знайдіть значення виразу в годинах: 88. Периметр трикутника дорівнює Знайдіть сторону трикутника, якщо дві інші його сторони дорівнюють 89. Периметр квадрата дорівнює Яким стане […]...

  8. Арифметичні дії додавання і віднімання Арифметичні дії додавання і віднімання 1 Обчисли. 2 Згадай закони додавання; правила додавання і віднімання. Визнач без обчислень істинність або хибність поданих рівностей. Поясни свої міркування. 5 867 – (1 329 + 2 867) = (5 867 – 2 867) – 1 329 (32 405 + 16 000) + 14 000 = 32 405 + […]...

  9. Окремі випадки множення десяткових дробів Розділ 2 ДРОБОВІ ЧИСЛА І Дії З НИМИ § 39.Окремі випадки множення десяткових дробів Помножимо за правилом множення десяткових дробів 5,725 на 10. Маємо помножити 5725 на 10, отримаємо 57 250, відокремлюємо справа комою три десяткових знаки. Отже, 5,725 ∙ 10 = 57,250 = 57,25. Аналогічно можна отримати 5,725 ∙ 100 = 572,5; 5,725 ∙ […]...

  10. Розв’язування вправ на додавання десяткових дробів Урок № 15 Тема. Розв’язування вправ на додавання десяткових дробів Мета уроку. Сформувати в учнів навички застосування законів додавання та прийомів раціоналізації додавання десяткових дробів. Хід роботи І. Актуалізація опорних знань учнів 1. Перевірка домашнього завдання. 2. Усні вправи. Гра “Кращий обчислювач”. Кожний учень підготував 3-4 приклади додавання десяткових дробів для усного обчислення. Клас ділиться […]...

  11. ДОДАВАННЯ І ВІДНІМАННЯ ДРОБІВ Розділ 2 ЗВИЧАЙНІ ДРОБИ ТА ДІЇ З НИМИ § 8 ДОДАВАННЯ І ВІДНІМАННЯ ДРОБІВ Ви вже знаете, як додавати і віднімати натуральні числа та дроби з однаковими знаменниками. Дроби з різними знаменниками також можна додавати й віднімати. Розглянемо задачу. Задача 1 . Мама купила дітям молочний шоколад, у якому 18 часточок. Тетянка сказала, що з’їла […]...

  12. Додавання і віднімання мішаних чисел Розділ 2 Звичайні дроби §11. Додавання і віднімання мішаних чисел Переставна та сполучна властивості додавання дають можливість звести додавання мішаних чисел до додавання їх цілих частин і додавання їх дробових частин. Якщо при додаванні дробових частин отримуємо неправильний дріб, то у цьому разі з нього виділяють цілу частину і додають її до цілої частини, яка […]...

  13. ПИСЬМОВЕ ДОДАВАННЯ Й ВІДНІМАННЯ ЧИСЕЛ ПОВТОРЕННЯ МАТЕРІАЛУ ЗА 3 КЛАС ПИСЬМОВЕ ДОДАВАННЯ Й ВІДНІМАННЯ ЧИСЕЛ 39. Розв’яжи задачу складанням виразу. У хорі Будинку творчості 85 дітей, у гуртку з моделювання на 39 дітей менше, ніж у хорі, а в танцювальних колективах на 19 дітей більше, ніж у хорі й гуртку з моделювання разом. Скільки дітей займаються в танцювальних колективах? 40. […]...

  14. Контрольна робота по темі: “Множення десяткових дробів” Урок № 32 Тема. Контрольна робота по темі: “Множення десяткових дробів” Мета: Перевірити, як учні засвоїли матеріал по темі: “Множення десяткових дробів” І Варіант 1. Обчислити: А) 0,036×3,5; Б)38,57×1000; В) 2,68×0,01. 2. Знайти значення виразу: (14 – 12,6)×4,3 + 1,08×1,2. 3.* Розв’язати рівняння: (х – 4,7) : 3,4 = 12,92. 4.* Човен плив 2,2 години […]...

  15. Одиниці часу. Додавання і віднімання іменованих чисел Одиниці часу. Додавання і віднімання іменованих чисел 1 Згадай відомі тобі одиниці часу. Як вони співвідносяться? 2 Знайди дріб від числа. 3 Знайди число за величиною його дробу, якщо його: Становлять 72 с; Становлять 84 хв; 15 Становлять 90 год; З Становлять 1 рік. 4 Заміни більші одиниці часу меншими. 5 Заміни менші одиниці часу […]...

  16. ДОДАВАННЯ І ВІДНІМАННЯ ДРОБІВ З ОДНАКОВИМИ ЗНАМЕННИКАМИ РОЗДІЛ 6 ДІЇ ПЕРШОГО СТУПЕНЯ ЗІ ЗВИЧАЙНИМИ ДРОБАМИ З ОДНАКОВИМИ ЗНАМЕННИКАМИ У розділі дізнаєтесь: Як додавати і віднімати дроби з однаковими знаменниками; Що таке доповнення правильного дробу до одиниці; Як віднімати правильний дріб від натурального числа; Які правила додавання і віднімання мішаних чисел; Як застосувати вивчений матеріал на практиці § 26. ДОДАВАННЯ І ВІДНІМАННЯ ДРОБІВ […]...

  17. Порівняння, додавання та віднімання дробів – Додавання і віднімання звичайних дробів Математика – Алгебра Додавання і віднімання звичайних дробів Порівняння, додавання та віднімання дробів Щоб виконати порівняння, додавання, віднімання дробів із різними знаменниками, треба звести їх до найменшого спільного знаменника, а потім виконати потрібну дію за аналогічним правилом для дробів з однаковими знаменниками. Завжди треба звертати увагу, чи мож­на спростити отримане число: виділити цілу частину або […]...

  18. Задачі і рівняння на додавання і віднімання дробів. Порівняння дробів. Основна властивість дробу Урок № 22 Тема. Задачі і рівняння на додавання і віднімання дробів. Порівняння дробів. Основна властивість дробу Мета: підготовити учнів до виконання тематичної контрольної роботи. Тип уроку: узагальнення та систематизації знань. Хід уроку I. Перевірка домашнього завдання @Урок є підсумковим з теми “Порівняння, додавання і віднімання дробових чисел”, тому вчитель, враховуючи особливості кожного класу, звертає […]...

  19. Віднімання десяткових дробів Урок № 18 Тема. Віднімання десяткових дробів Мета уроку. Вироблення в учнів навиків віднімання десяткових дробів. Тип уроку. Комбінований. Хід уроку І. Перевірка домашнього завдання З метою економії часу біля дошки учні пояснюють розв’язування № 1187 і №1189. В решті у учнів перевіряється наявність домашнього завдання в зошитах. ІІ. Актуалізація знань і вмінь учнів; вивчення […]...

  20. Повторення. Арифметичні дії додавання, віднімання, множення і ділення Повторення. Арифметичні дії додавання, віднімання, множення і ділення 1 Розкажи, що тобі відомо про арифметичні дії додавання, віднімання, множення і ділення. Згадай закони і правила арифметичних дій. 2 Обчисли зручним способом, за бажанням використовуючи правила та закони арифметичних дій. (56 738 + 42 607) – 24 738 (125 ∙ 56) ∙ 8 83 129 – […]...

  21. Множення і ділення десяткових дробів Урок 110 Тема. Множення і ділення десяткових дробів Мета: перевірити якість засвоєння програмних знань з теми та визначити рівень сформованості умінь і навичок. Тип уроку: перевірка й корекція знань, умінь і навичок. Хід уроку I. Перевірка домашнього завдання Зібрати робочі зошити з тематичним оцінюванням № 8. II. Умови тематичної контрольної роботи № 8 Варіант 1 […]...

  22. Додавання десяткових дробів Урок № 16 Тема. Додавання десяткових дробів Мета уроку. Узагальнити знання учнів з теми, формувати вміння аналізувати відповіді однокласників, доводити власну точку зору, розвивати логічне мислення, культуру математичного мовлення, спостережливість, уважність, терпіння, уміння зосереджуватись, виховувати дисциплінованість. Обладнання: Індивідуальні картки із завданнями, наочні картинки на дошці. Хід роботи І. Мотивація навчальної діяльності Учитель. Сьогодні ми проведемо […]...

  23. Віднімання десяткових дробів. Розв’язування задач Урок № 19 Тема. Віднімання десяткових дробів. Розв’язування задач Мета уроку. Вироблення навиків розв’язування задач та віднімання десяткових дробів, розвиток логічного мислення. Тип уроку. Комбінований. Хід уроку І. Перевірка домашнього завдання 1. Що називають рівнянням? 2. Що називають коренем рівняння? 3. Що означає розв’язати рівняння? 4. Біля дошки учень пояснює розв’язання №1202. ІІ. Розв’язання задач […]...

  24. Зведення дробів до спільного знаменника – Додавання і віднімання звичайних дробів Математика – Алгебра Додавання і віднімання звичайних дробів Зведення дробів до спільного знаменника Будь-які дроби можна звести до спільного знаменника. Таким знаменником може бути будь-яке спільне кратне знаменників цих дробів. Зрозуміло, що звичайно обирають найменший спільний кратний знаменник (НСЗ). Щоб звести дроби до найменшого спільного знаменника, треба: 1) знайти найменше спільне кратне знаменників; 2) знайти […]...

  25. Порівняння десяткових дробів Розділ 2 ДРОБОВІ ЧИСЛА І Дії З НИМИ § 35. Порівняння десяткових дробів Важливим є питання порівняння десяткових дробів. Почнемо з такого прикладу. Відомо, що 3 дм = 30 см = 300 мм. Виразивши 3 дм, 30 см і 300 мм у метрах, матимемо: 3 дм = 0,3 м; 30 см = 0,30 м; 300 […]...

  26. Десятковий дріб. Запис десяткових дробів Розділ 2 ДРОБОВІ ЧИСЛА І Дії З НИМИ § 34. Десятковий дріб. Запис десяткових дробів Нарівні зі звичайними дробами для запису дробових чисел використовують десяткові дроби. Приклад 1. Виразимо відстань 7 дм 3 см у дециметрах. Оскільки Тому Приклад 2. Знаменник дробової частини числа дорівнює 10, а числа дорівнює 100. Числа зі знаменниками 10, 100, […]...

  27. Округлення натуральних чисел і десяткових дробів Розділ 2 ДРОБОВІ ЧИСЛА І Дії З НИМИ § 36. Округлення натуральних чисел і десяткових дробів Припустимо, наприклад, що кількість учнів у школі на 1 вересня становить 1682. Однак через деякий час кількість учнів у школі зміниться, а тому назване число стане неправильним. У ньому зміниться цифра розрядів одиниць, а можливо, і десятків. Тому можна […]...

  28. Письмове додавання та віднімання багатоцифрових чисел Розділ IV Арифметичні дії з багатоцифровими числами Письмове додавання та віднімання багатоцифрових чисел 673. Математична розминка. Обчисли частку, одержану відділення числа 824 на число, що дорівнює кількості його десятків. Обчисли частку, одержану відділення числа 60 300 на число, що дорівнює кількості його сотень. Обчисли частку, одержану від ділення числа 8100 на число, що дорівнює сумі […]...

  29. Додавання і віднімання дробів з однаковими знаменниками Урок № 5 Тема. Додавання і віднімання дробів з однаковими знаменниками Мета. Поглибити знання учнів про дріб; вчити додавати й віднімати дроби з однаковими знаменниками. Розвивати обчислювальні навички, культуру математичної мови і записів. Виховувати самостійність, інтерес до математики. Тип уроку: засвоєння нових знань. Обладнання: картки з числами, таблиці: “Додавання дробів з однаковими знаменниками”, “Віднімання дробів […]...

  30. ДОДАВАННЯ І ВІДНІМАННЯ КРУГЛИХ БАГАТОЦИФРОВИХ ЧИСЕЛ ЗАСТОСУВАННЯ НУМЕРАЦІЇ ДО ВИКОНАННЯ ДІЙ ДОДАВАННЯ І ВІДНІМАННЯ КРУГЛИХ БАГАТОЦИФРОВИХ ЧИСЕЛ 496. 5 тис. + 4 тис. 2 сот. + 9 сот. 30 дес. + 20 дес. 5 000 + 4 000 8 сот. – 3 сот. 12 сот. – 3 сот. 3 800 + 1 000 3 800 + 100 3 800 + 20 […]...

  31. Додавання натуральних чисел. Властивості додавання Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 3. Додавання натуральних чисел. Властивості додавання З початкових класів відомо, як додавати невеликі натуральні числа. Розглянемо задачу. Задача. У 5-А класі 27 учнів, а в 5-Б – 29 учнів. Скільки учнів у двох класах? Розв’язання. 27 + 29 = 56. Ця задача […]...

  32. ДІЛЕННЯ ДЕСЯТКОВИХ ДРОБІВ РОЗДІЛ 7 ДЕСЯТКОВІ ДРОБИ ТА ДІЇ З НИМИ § 32. ДІЛЕННЯ ДЕСЯТКОВИХ ДРОБІВ Ви знаєте, що дія ділення є оберненою до дії множення. Це стосується не лише натуральних чисел, а й дробів. Розглянемо задачі, обернені до тих, що розв’язали в попередньому параграфі. Задача 1. Для поїздки на природу купили 3 упаковки зефіру загальною масою 1,5 […]...

  33. ДОДАВАННЯ І ВІДНІМАННЯ ПО 4. ЗНАХОДЖЕННЯ НЕВІДОМИХ КОМПОНЕНТІВ ДІЙ ДОДАВАННЯ ТА ВІДНІМАННЯ. РОЗВ’ЯЗУВАННЯ І ПОРІВНЯННЯ ЗАДАЧ. ПОБУДОВА ВІДРІЗКІВ ТАБЛИЧНЕ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ У МЕЖАХ 10 Урок 61. ДОДАВАННЯ І ВІДНІМАННЯ ПО 4. ЗНАХОДЖЕННЯ НЕВІДОМИХ КОМПОНЕНТІВ ДІЙ ДОДАВАННЯ ТА ВІДНІМАННЯ. РОЗВ’ЯЗУВАННЯ І ПОРІВНЯННЯ ЗАДАЧ. ПОБУДОВА ВІДРІЗКІВ Мета: вправляти учнів у засвоєнні табличних випадків додавання і віднімання числа 4, додаванні і відніманні по 4, знаходженні невідомих компонентів дій додавання та віднімання; вчити розв’язувати і […]...

  34. Основна властивість дробу – Додавання і віднімання звичайних дробів Математика – Алгебра Додавання і віднімання звичайних дробів Основна властивість дробу Якщо чисельник і знаменник дробу помножити або поділити на одне й те саме натуральне число, дістанемо дріб, що дорівнює даному. Рівні дроби – це різні записи одного й того ж числа. Застосування основної властивості дробу Скорочення дробу Ділення чисельника і знаменника дробу на їхній […]...

  35. ПЕРЕВІРКА ДОДАВАННЯ Й ВІДНІМАННЯ ЧИСЕЛ ДІЇ З БАГАТОЦИФРОВИМИ ЧИСЛАМИ. ПИСЬМОВЕ ДОДАВАННЯ І ВІДНІМАННЯ ПЕРЕВІРКА ДОДАВАННЯ Й ВІДНІМАННЯ ЧИСЕЛ 571. Чи утворюють числа 17 359, 2 568 і 19 927 при додаванні і відніманні “родину”? Як пов’язані між собою дії додавання і віднімання? 572. Пригадай способи: А) перевірки додавання. 1. а + b = b + а 2. 3. прогнозування результату […]...

  36. Перетворення звичайних дробів на десяткові – Додавання і віднімання звичайних дробів Математика – Алгебра Додавання і віднімання звичайних дробів Перетворення звичайних дробів на десяткові Щоб перетворити звичайний дріб на десятковий, треба ділити чисельник на знаменник за правилом ділення десяткових дробів. У деяких випадках отримаємо скінченний десятковий дріб. Приклад . В інших випадках дістанемо нескінченний періодичний десятковий дріб, тобто такий, у записі якого одна чи декілька цифр […]...

  37. Раціональні вирази. Основна властивість дробу. Додавання і віднімання дробів Урок № 11 Тема. Раціональні вирази. Основна властивість дробу. Додавання і віднімання дробів Мета: перевірити рівень знань та вмінь учнів, набутих ними піл час вивчення теми “Раціональні вирази”. Тип уроку: контроль знань та вмінь. Хід уроку I. Організаційний етап II. Перевірка домашнього завдання Зібрати зошити з виконаною домашньою контрольною роботою № 1 (роботу перевірити та […]...

  38. Додавання та віднімання дробів – Раціональні вирази Математика – Алгебра Раціональні вирази Додавання та віднімання дробів 1. Щоб додати (відняти) дроби з однаковими знаменниками, треба додати (відняти) їхні чисельники, а знаменник залишити той самий. Наприклад: 1) . 2) . 2. Якщо треба знайти суму або різницю дробів з різними знаменниками, то спочатку дроби зводять до спільного знаменника. Приклади 1) ; спільний знаменник […]...

  39. Strong>Додавання і віднімання величин 4. Додавання і віднімання багатоцифрових чисел Додавання і віднімання величин 473. 50 кг + 12 кг 240 кг + 37 кг 135 кг + 98 кг 135 кг – 49 кг 157 кг – 95 кг 235 г – 79 г Розглянь зразки додавання величин. 26 т 349 кг + 8 т 652 кг = […]...

  40. ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ. ЗАДАЧІ НА ДВІ ДІЇ. ВИРАЗИ З ДУЖКАМИ ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ 82. Поясни прийоми додавання і віднімання чисел з переходом через розряд. Перевір результати обчислень за таблицями. Розкажи їх із пам’яті. 83. 11 – 2 – 4 14 – 5 + 2 14 – 10 + 6 39 – […]...

Ви зараз читаєте: Додавання і віднімання десяткових дробів
«
»