Головна ⇒ 📌Математика ⇒ ДОДАВАННЯ І ВІДНІМАННЯ ДРОБІВ

ДОДАВАННЯ І ВІДНІМАННЯ ДРОБІВ

Розділ 2 ЗВИЧАЙНІ ДРОБИ ТА ДІЇ З НИМИ

§ 8 ДОДАВАННЯ І ВІДНІМАННЯ ДРОБІВ

Ви вже знаете, як додавати і віднімати натуральні числа та дроби з однаковими знаменниками. Дроби з різними знаменниками також можна додавати й віднімати. Розглянемо задачу.

Задача 1 . Мама купила дітям молочний шоколад, у якому 18 часточок. Тетянка сказала, що з’їла б 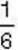плитки шоколаду, а Іванко сказав, що з’їв би 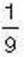плитки (мал. б). Яку частину плитки шоколаду з’їли б Тетянка та Іванко разом?

class=""/>

Мал. б

Розв’язання. Тетянка та Іванко міряли плитку шоколаду різники мірками: Тетянка міряла шостими частинами, а Іванко – дев’ятими. Щоб знайти суму 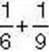, треба кожний доданок подати в одних і тих самих одиницях вимірювання. Зрозуміло, що дня плитки шоколаду такою міркою є часточка, або 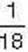плитки. Тоді 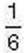плитки містить 3 часточки, тобто дорівнює 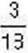плитки шоколаду, а 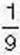плитки містить 2 часточки, тобто дорівнює 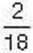плитки шоколад. Разом це становить 5 часточок,

або

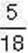плитки шоколаду. Отже, діти з’їли б

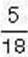плитки шоколаду.

Розв’язуючи задачу, ми, по суті, виконали дію додавання дробів з однаковими знаменниками. Спробуйте самостійно сформулювати відповідне правило та порівняйте його з наведеним у підручнику.

Запамятайте!

Правило додавання дробів з різними знаменниками. Щоб знайти суму двох дробів з різними знаменниками, треба:

1) звести дані дроби до спільного знаменника;

2) спільний знаменник записати в знаменнику суми;

3) додати нові чисельники і результат записати в чисельнику суми;

4) якщо можливо, то скоротити отриманий у сумі дріб та виділити цілу частину.

Наприклад:

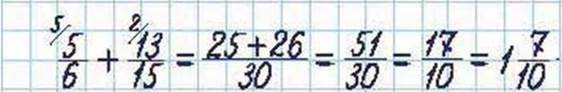
При додаванні дробів з різними знаменниками, так само, які при додаванні натуральних чисел, справджуються переставний і сполучний закони додавання.

Задача 2. Тетянка та Іванко з’їли плитки шоколаду, у якій загалом 18 часточок. Тетянка з’їла 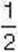плитки шоколаду, а іншу частину з’їв Іванко. Яку частину плитки з ‘їв Іванко?

Розв’язання. Щоб розв’язати задачу, треба знайти різницю дробів 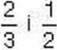. Оскільки плитки містять 12 часточок, тобто дорівнюють 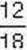плитки, а 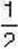плитки містить 9 часточок, тобто дорівнює 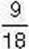плитки, то 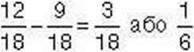плитки шоколаду.

Отже, Іванко з’їв плитки шоколаду.

Сформулюємо правило віднімання дробів з різними знаменниками.

Запам’ятайте!

Правило віднімання дробів з різним и знаменника ми

Щоб знайти різницю двох дробів з різними знаменниками, треба:

1) звести дані дроби до спільного знаменника;

2) спільний знаменник записати в знаменнику різниці;

3) відняти нові чисельники й результат записати в чисельнику різниці;

4) якщо можливо, то отриманий у різниці дріб скоротити та виділити цілу частину.

Задача 3. Обчисліть: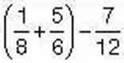

Розв’язання. Задачу можна розв’язати двома способами.

Спосіб 1.

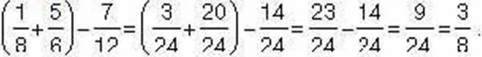
Спосіб 2.

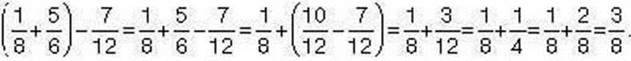
? Чи можна додавати (віднімати) два мішані числа, знаменники дробових частин яких різні? Так. При цьому дробові частини зводять до спільного знаменника. Розглянемо приклад.

Задача 4 . Обчисліть: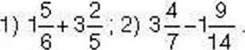

Розв’язання. 1, Задачу можна розв’язати двома способами.

Спосіб 1.

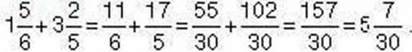
Спосіб 2.

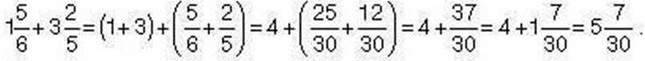
2. Скористаємося другим способом:

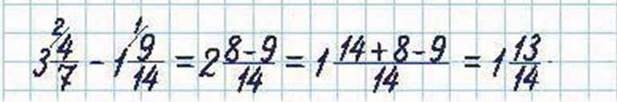
Існує багато різних математичних фокусів, які ви можете запропонувати своїм друзям чи знайомим. Ось один із них. Завдання. Потрібно задумати будь-яке натуральне число, потім додати до нього наступне по порядку, потім до суми додати 9, поділити отримане число навпіл і від отриманого результату відняти задумане число. Яке дістанемо число? Ви легко можете назвати число, яке вийшло в результаті цих дій – це число 5. Спробуйте придумати свій математичний фокус і запропонуйте його друзям.

ПРИГАДАЙТЕ ГОЛОВНЕ

1. Сформулюйте правило додавання двох дробів з різними знаменниками.

2. Сформулюйте правило віднімання двох дробів з різними знаменниками.

3. Поясніть, я к додати або відняти два мішані числа, дробові частини яких мають різні знаменники.

РОЗВ’ЯЖІТЬ ЗАДАЧІ

277′. Якщо до 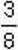додати 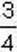, то отримаємо дріб, у якому:

1) знаменник дорівнює: а) 4; б) 2; в) 8; г) 12;

2) чисельник дорівнює: а) 6; б) 9; в) 12; г) 16.

278′. Чи правильно, що сумою дробів 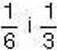є дріб:

279′. Якщо від , то в результаті отримаємо дріб, у якому:

1) знаменник дорівнює: а) 2; б) 4; в) 6; г) 8;

2) чисельник дорівнює: а) 6; б) 3; в) 8; г) 1.

280′. Чи правильного 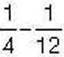дорівнює:

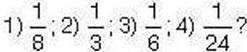
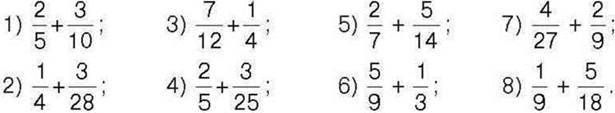
282°. Обчисліть:

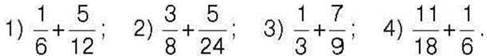
283°. Порівняйте:

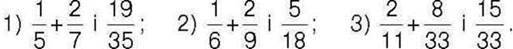
284°. Порівняйте:

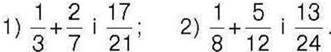
285°. Розмістіть на координатному промені точки, координати яких дорівнюють значенням виразів:

286°. Розмістіть на координатному промені точки, координати яких дорівнюють значенням виразів:

287°. Знайдіть зменшуване, якщо різниця дорівнює 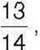а від’ємник –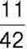

288°. Знайдіть суму, якщо перший доданок дорівнює 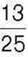, а другий –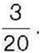

289°. Розв’яжіть рівняння:

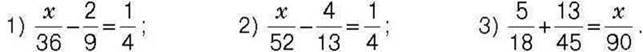
290°. Розв’яжіть рівняння:

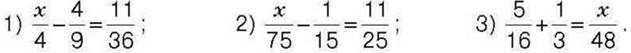
291°. Обчисліть:

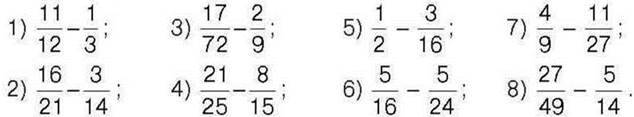
293°. Порівняйте:

294°. Порівняйте:

295°. Розмістіть на координатному промені точки, координати яких дорівнюють значенням виразів:

296°. Розмістіть на координатному промені точки, координати яких дорівнюють значенням виразів:

297°. Сума двох дробів дорівнює 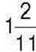, а один із доданків – 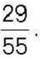Знайдіть інший доданок.

298°. Зменшуване дорівнює 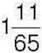, а різниця – 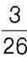. Знайдіть від’ємник.

299°. Сума трьох дробів дорівнює 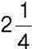, а два з цих дробів – це числа 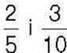. Знайдіть невідомий дріб.

300°. Обчисліть:

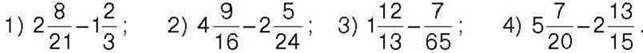
301°. Обчисліть:

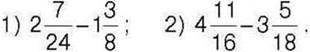
302°. За день у магазині продали 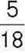т фруктів. З них 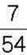т становили яблука, а решту – сливи. Скільки тон слив продали в магазині?

303°. Від шматка тканини завдовжки 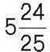м відрізали шматок завдовжки 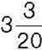м. Скільки метрів тканини залишилось?

304°. З кг бананів коштують 35 грн, а 5 кг апельсинів – 37 грн. Наскільки 1 кг бананів дорожчий, ніж 1 кг апельсинів?

305°. Знайдіть середнє арифметичне таких наборів чисел: 4, 5, 7 та 3, 5, 8, 9. Яке з отриманих середніх арифметичних більше і на скільки?

306. Обчисліть:

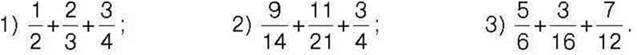
307. Обчисліть:

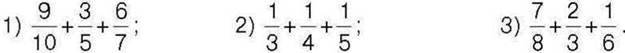
308. Розмістіть суми в порядку зростання їх значень:

309. Розмістіть суми в порядку спадання їх значень:

310. Розв’яжіть рівняння:

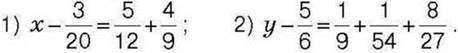
311. Розв’яжіть рівняння:

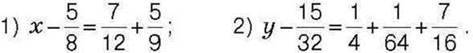
312. Обчисліть:

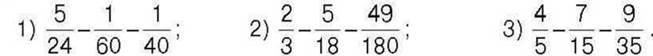
313. Обчисліть:

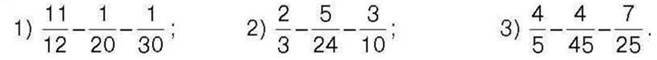
314. Обчисліть:

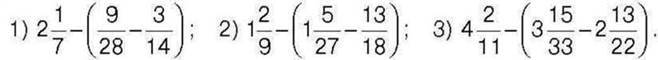
315. Обчисліть:

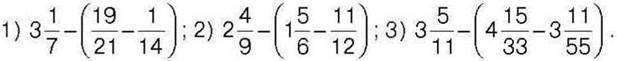
316. Розв’яжіть рівняння:

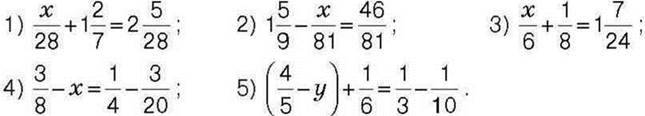
317. Розв’яжіть рівняння:

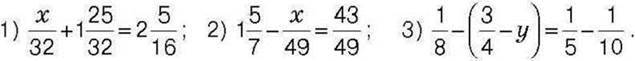
318. Відрізок АВ поділено на частини точками М і N так, що відрізок AM становить 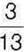відрізка АВ, а відрізок MN – 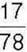відрізка АВ. Яку частину відрізка АВ становить відрізок NB?

319. Відрізок MN поділено на частини точками А і С так, що відрізок МА становить 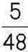відрізка MN, а відрізок АС – 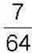відрізка MN. Яку частину відрізка MN становить відрізок СN?

320. На скільки різниця 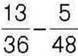менша від числа 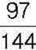і більша за різницю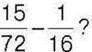

321. Марійка задумала деяке число, яке спочатку збільшила на 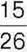, а потім – ще на 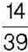. У результаті вона отримала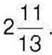

Яке число задумала Марійка?

322. Андрій задумав деяке число, яке спочатку збільшив на 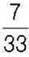, а потім зменшив на 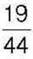. У результаті він отримав 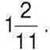Яке число задумав Андрій?

323*. Доведіть, що 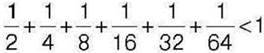. На скільки значення лівої частини нерівності менше від значення правої?

324*. Дано натуральне число а. Що більше:

ЗАСТОСУЙТЕ НА ПРАКТИЦІ

325. Тетянка віддала Марійці 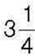грн, тоді в кожної з дівчаток стало по 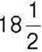грн. Скільки грошей було в кожної дівчинки спочатку?

326. На шкільних спортивних змаганнях Сергійко пробіг 1 км за 3 хв 5 с, а Андрійко пробіг 1 км за 3 хв 10 с. Знайдіть швидкість кожного хлопчика (у метрах за секунду). На скільки швидкість Сергійка більша за швидкість Андрійка?

ЗАДАЧІ НА ПОВТОРЕННЯ

327. Обчисліть: 1) 4 % від 24; 2) 15% від 54; 3)30% від 3,6.

328. Обчисліть периметр п’ятикутника, якщо його найменша сторона дорівнює 3,4 см, а кожна наступна – на 1,8 см більша за попередню.