Довжина кола. Число n
Урок № 5 6
Тема. Довжина кола. Число n
Мета: повторити відомості, які учні мають з початкової школи про коло; сформувати більш строге геометричне уявлення про коло, його елементи та співвідношення між ними; дати зміст поняття “довжина” кола і виробити вміння знаходити довжину кола за відомим радіусом або діаметром та розв’язувати обернену задачу.
Тип уроку: засвоєння нових знань, умінь та навичок.
Хід уроку
I. Перевірка домашнього завдання
@ Збираємо творчі завдання.
II. Актуалізація опорних знань
Усні вправи
1. Обчисліть: |
|
|
|
2. Серед фігур, зображених на рисунку, вкажіть ті, назви яких вам відомі. Назвіть ці фігури.

3. Точка М належить відрізку АВ, довжина якого 25 см. Знайдіть довжини відрізків AM і ВМ, якщо: а) точка М – середина відрізка; б) AM більше за ВМ у 4 рази.
III. Формування знань
@ Поняття кола знайоме учням ще з початкової школи. Але оскільки ми до нього ще не звертались (ані в 5 класі, ані в 6 класі),
1. Уявлення про коло
Нагадаймо учням, що математика – це не тільки наука про числа і дії з ними (до речі, цей розділ називається арифметикою); математика вивчає ще геометричні фігури і їх властивості (див. усні вправи) (цей розділ математики називається геометрією). Серед багатьох інших геометричних фігур ми розглянемо дуже цікаву фігуру – коло.
Як накреслити коло? (Беремо циркуль і послідовно виконуємо дії: вибираємо точку, позначаємо її зазвичай літерою О; ставимо вістря циркуля в т. О й проводимо іншим кінцем циркуля замкнену лінію – це і є коло).
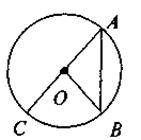
Після цього називаємо елементи кола.
Т. О – центр кола;
ОА, ОВ – радіуси кола:
ОА = OB = R;
АВ – хорда;
АС – діаметр:
АС = D.
Звертаємо увагу на те, що в будь-якому колі можна провести безліч радіусів, хорд, діаметрів! (До речі, вимагати від шестикласників заучувати означення кола та всіх його елементів не треба – достатньо володіння темою на інтуїтивному рівні і вироблення вміння називати зображені на готовому рисунку елементи кола).
2. Співвідношення між діаметром і радіусом кола
На рисунку бачимо: на АС лежить т. О, причому AO – OC = R, отже, О – середина АС, тому АО = CO = АС : 2, тобто R = D : 2, звідки D = 2R.
3. Довжина кола, число n
@ Mи з’ясували, що коло – це лінія, яку рисує кінець циркуля, вістря якого знаходиться у т. О – центрі кола. Але ж кожна лінія має довжину. Як же знайти довжину кола? Чи можна її виміряти (обчислити)?
Проведемо такий експеримент. Поставте круглу склянку на аркуш паперу та обведіть її олівцем. Отримаємо коло. Візьміть нитку та обведіть нею склянку. Випряміть нитку та виміряйте її довжину. Виміряйте діаметр кола. Знайдіть відношення довжини кола до його діаметра.
Висновок. Довжина кола приблизно у 3 рази більша за його діаметр; отже, C = nD або C = 2nR.
Після цього розповідаємо дітям про число n. (Можна додати цікаву інформацію про те, що позначення літерою n не випадкове, бо це перша літера в грецькому слові????????? (“периферія”) – коло, круг, та про те, як можна запам’ятати перші шість значущих цифр числа n – (рос. мовою)
Это | Я | Знаю | И | Помню | Прекрасно… |
3 | 1 | 4 | 1 | 5 | 9… |
4. Висновок. Насамкінець ми маємо:
1) уявлення про коло, радіус кола, діаметр кола;
2) уявлення про те, що собою являє довжина кола; співвідношення між С (довжиною кола) і R або D (радіусом або діаметром кола), а в зошитах учнів короткі записи у вигляді конспекту 26.
IV. Засвоєння вмінь
@ Усі задачі, які розв’язуємо на уроці можна умовно поділити на 2 групи:
А) задачі на застосування формули D = 2R;
Б) задачі на застосування формули C = nD.
Але бажано дати задачі різних рівнів на формування вміння працювати із цими формулами.
Конспект 26 | ||
Коло, довжина кола | ||
О – центр кола; OA = OB = R – радіуси; АС = D – діаметр; АВ – хорда; R = D : 2; D = 2R; C = nD; C = 2nR
|
| Приклади 1) Якщо R = 5 см, То D = 2R = 2-5 = 10см; 2) якщо D = 5 см, То R = 5:2 = 5:2 = 2,5 см; 3) якщо D = 5 см, То С = nD = 5? (см); 4) якщо R = 5 см, То С = 2nR = 2-n-5 = 10n |
Усні вправи
1. Назвіть радіуси, діаметр, хорду кола (див. рис).
2. Знайдіть радіус і довжину кола діаметра 10 см.
3. Знайдіть довжину діаметра і кола радіуса 5 дм.
Письмові вправи
1. Задачі на застосування формули D = 2R. Знайдіть радіус кола, якщо:
А) його діаметр 2 см; 2 м 3 см; 2,6 дм; 1,5 дм;
Б) його діаметр більший за радіус на 5 дм; 3 м; 2,5 см.
2. Задачі на застосування формули C = nD = 2nR.
1) Знайдіть довжину кола, якщо:
А) діаметр 2,5 см; 24 см; 0,32 м;
Б) радіус 5 см; 4, 2 см; 0,8 дм.
2) Довжина кола дорівнює 33 м. Знайдіть діаметр кола ( ).
).
– Обернена (! бажано показати, що з формули C = nD можна виразити 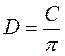 , а з формули С = 2nR
, а з формули С = 2nR 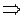
 ).
).
3. Якщо вистачить часу, хотілося б розв’язати такі задачі (повторити, що t = s : v; P – сума довжин усіх сторін).
А) За скільки часу можна облетіти на літаку Землю вздовж екватора на висоті 10 км, рухаючись зі швидкістю 1200 км/год? Результат округліть до 0,1 год. ( Радіус екватора наближено дорівнює 6370 км).
Б) Довжина кола збільшилась з 157 см до 226,08 см. На скільки збільшився радіус кола?
В) Із прямокутника вирізали півкруг (рис).
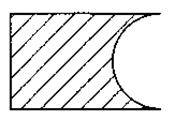
Зробіть необхідні вимірювання і знайдіть периметр утвореної фігури.
V. Підсумки уроку
“Німий” диктант
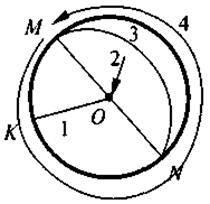
Учитель ще раз нагадує зміст вивченого на уроці матеріалу у формі “німого” диктанту: показує на заздалегідь заготовленому рисунку об’єкти, що вивчались на уроці, а учні в письмовій чи усній формі відповідають на запитання:
1 – радіус ОК;
2 – центр О;
3 – діаметр MN;
4 – коло.
N – MN – ? (С – довжина кола)
VI. Домашнє завдання
Задача 1. Знайдіть довжину кола: а) діаметра 3 см; 0,6 дм; 0,12 м; б) радіуса 6 см; 1,2 дм; 2,3 м.
Задача 2. Довжина кола дорівнює 2,2 м. Знайдіть діаметр кола ( ).
).
Задача 3. Радіус кола збільшили з 10 см до 11 см. На скільки збільшилась довжина кола?
Задача 4. Діаметр колеса тепловоза дорівнює 80 см. За 2 хв колесо робить 800 обертів. Яка швидкість тепловоза в кілометрах за годину? Результат округліть до десятих км/год.
Задача 5. У парку першого дня посадили 96 дерев, а другого – 72 дерева, що становить 80 % від кількості дерев, посаджених третього дня. Скільки дерев посадили за три дні?
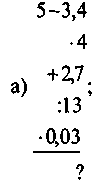
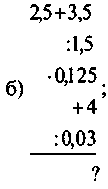
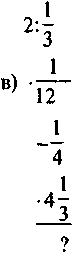
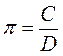 ; С – довжина кола.
; С – довжина кола. 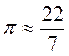 ; n? 3,14
; n? 3,14