Електромагнітна теорія світла
ФІЗИКА
Частина 4
ОПТИКА. СПЕЦІАЛЬНА ТЕОРІЯ ВІДНОСНОСТІ
Розділ 10 ЕЛЕКТРОМАГНІТНА ТЕОРІЯ СВІТЛА
10.2. Електромагнітна теорія світла
У середині XIX ст. встановлено чимало фактів, що вказують на зв’язок електричних і магнітних явищ з оптичними.
Англійський фізик М. Фарадей установив зв’язок електрики й магнетизму, а 1845 р. відкрив обертання площини поляризації в магнітному полі. Розвиваючи уявлення А. Ампера і М. Фарадея про взаємозв’язок електричних і магнітних явищ, Дж. Максвелл відкрив електромагнітне поле і встановив
Якщо в просторі змінюється електричне поле, то внаслідок індукції воно спричинює в цій області простору і прилеглих до нього областях змінне магнітне поле. Змінне магнітне поле, у свою чергу, породжує змінне електричне поле і т. д. Сукупність таких змінних електричних і магнітних полів створює електромагнітне поле. Виникнувши в певному місці, змінне електромагнітне поле передається від однієї точки простору до іншої з певною швидкістю. Цей процес поширення змінного електромагнітного поля в просторі називають електромагнітною хвилею.
Напрям векторів напруженості електричного і магнітного полів, а також напрям поширення електромагнітних хвиль взаємно перпендикулярні. Отже, електромагнітні хвилі – поперечні. На рис. 10.1 схематично зображено плоску електромагнітну хвилю. В цьому разі вектор напруженості електричного поля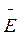 
коливається у вертикальній площині zОх, а вектор напруженості магнітного поля 
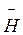в горизонтальній площині yОх.
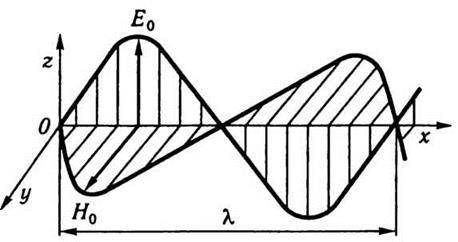
Рис. 10.1
Аналізуючи закон електромагнітної індукції М. Фарадея, Дж. Максвелл висунув гіпотезу, що змінне в часі магнітне поле породжує вихрове електричне, тобто силові лінії електричного поля замкнені й охоплюють силові лінії магнітного поля. Щоб формально узгодити свою теорію із законом збереження заряду, Дж. Максвеллу довелось припустити, що не тільки змінне в часі магнітне поле породжує вихрове електричне, а й навпаки: змінне в часі електричне поле породжує вихрове магнітне поле.
Точний запис сформульованого закону містить додаткове припущення про так званий струм зміщення, який Дж. Максвелл визначив як (локальну) похідну по часу від вектора електричної індукції І). Цю гіпотезу покладено в основу одного з рівнянь Максвелла, що цілком узгоджується з експериментом.
Отже, за Максвеллом, змінне в часі електричне й магнітне поля породжують одне одного, і цей процес може поширюватися від точки до точки в просторі, збуджуючи електромагнітні хвилі.
Основою теорії є рівняння Максвелла. У вченні про електромагнетизм ці рівняння відіграють таку саму роль, як і закони Ньютона в механіці або основні закони (принципи) в термодинаміці. Рівнянням Максвелла підлягає поширення електромагнітних хвиль.
У диференціальній формі рівняння Максвелла набувають вигляду
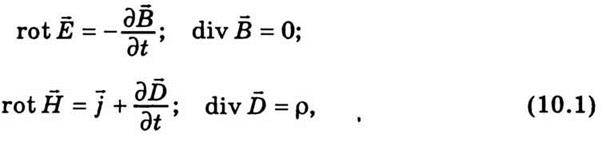
Де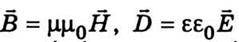 
(ε0 і μ0 – електрична і магнітна сталі, ε і μ – відносні діелектрична і магнітна проникності середовища),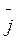 
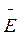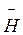– густина струму провідності; ρ – об’ємна густина електричних зарядів. Для з’ясування основних закономірностей, що характеризують поширення електромагнітних хвиль, розглянемо поширення плоскої електромагнітної хвилі в однорідному непровідному середовищі (ρ = 0, j = 0). Якщо вісь х напрямити перпендикулярно до хвильових поверхонь, то і , а отже, і їхні складові не залежатимуть від координат y та z, тому
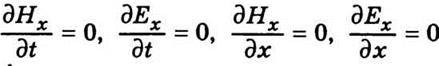
І рівняння (10.1) спрощуються
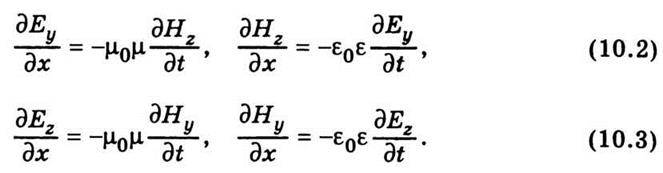
Отже, саме поле хвилі не має складової вздовж осі х, тобто вектори 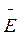і 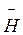перпендикулярні до напряму поширення хвилі. Рівняння (10.2) дають зв’язок між складовими Еу і Нz, а рівняння (10.3) зв’язують складові Еz і Ну. Щоб описати плоску електромагнітну хвилю, досить взяти одну із систем рівнянь, поклавши складові, що фігурують в іншій системі, такими, що дорівнюють нулю. Описуючи хвилю, візьмемо першу групу рівнянь (10.2), поклавши Еz = Ну = 0. Якщо здиференціювати перше рівняння (10.2) по х і врахувати, що
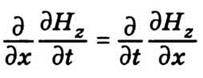
(це випливає із незалежності змінних х і t), то, підставивши потім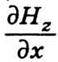 
з другого рівняння, дістанемо хвильове рівняння для Еy:
Диференціюючи по х друге рівняння (10.2), матимемо після аналогічних перетворень хвильове рівняння для Нz:
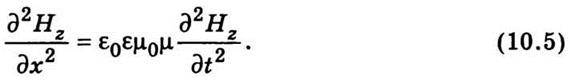
Оскільки інші складов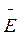і і 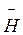дорівнюють нулю, то Е = Еу і Н = Нz. Остаточно рівняння для плоскої електромагнітної хвилі матимуть такий вигляд:
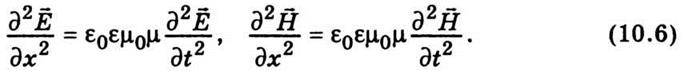
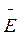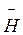Отже, обидва компоненти електромагнітного поля і описуються однаковим диференціальним рівнянням. Процеси, які описуються рівняннями (10.6), мають хвильовий характер. Зокрема, розв’язком рівняння (10.6) для складової електричного поля є така функція:
Цей вираз є рівнянням плоскої біжучої хвилі, що поширюється вздовж осі х з амплітудою Е0, періодом коливань Т і швидкістю поширення υ. Справді, якщо позначити
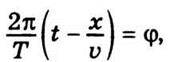
То рівняння (10.7) можна записати так:
Де φ – фаза хвилі.
Якщо розглядати хвильовий процес у будь-якій точці простору з часом, то ми маємо покласти х = const і вважати змінною лише величину t. Для спрощення покладемо х = 0. Тоді фаза залежатиме
Визначимо проміжок часу Δt, за який φ змінюється на 2π, а Е повторює своє значення, що відповідає моменту t. Скориставшись співвідношенням (10.9), маємо
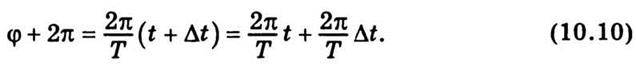
Звідси випливає, що зміна фази на величину 2π відбувається за Δt = Т. Отже, напруженість електричного поля повторює свої значення в даній точці простору через проміжки часу Т, тобто Т є періодом коливань вектора напруженості електричного поля . На рис. 10.2 зображено залежність вектора напруженості електричного поля від часу. Якщо графічно зобразити стан процесу в певний момент часу t = const, наприклад при t = t0, то утворений графік буде подібним до графіка на рис. 10.2, але змінною величиною в цьому разі стане координата х. Графік показує миттєве положення хвиль у момент часу t = t0 (рис. 10.3). Період зміни напруженості електричного поля 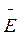в просторі можна знайти з таких умов. У точці х при t = t0 фаза матиме значення
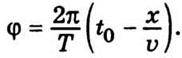
Більш віддалені точки хвилі відповідатимуть більш раннім моментам проходження їх через точку х = 0. Нехай на відстані Δх від точки х фаза зменшиться на 2π, тобто дорівнюватиме φ-2π. Тоді
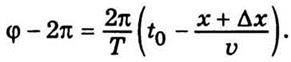
Звідси, враховуючи, що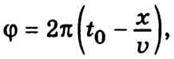 
Дістанемо
Оскільки при зміні φ на 2π вектор 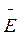здійснює повне коливання, то величина Δx: є періодом зміни функції 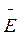в просторі й називається довжиною хвилі. Цю величину позначають літерою λ. Довжину хвилі можна виразити через швидкість її поширення і період коливань:
Довжиною хвилі є відстань, на яку поширюється хвильовий процес за час одного періоду коливань.
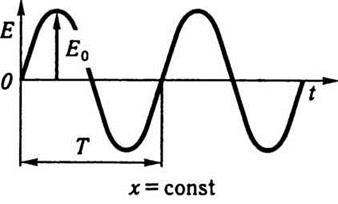
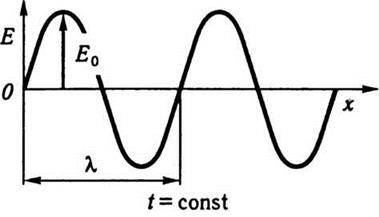
Рис. 10.2 Рис. 10.3
У. загальному випадку змінюються обидві величини, тобто t і х. Якщо спостерігати за якоюсь точкою хвилі, тоді слід вважати сталою величину φ:
Рівняння (10.13) для кожного моменту часу е рівнянням площини. Площини сталої фази є хвильовими поверхнями електромагнітної хвилі, тобто ці хвилі плоскі. В більш загальному випадку поверхня хвилі, тобто геометричне місце точок, де фаза хвилі залишається сталою, може бути більш складною поверхнею – сферою, еліпсоїдом, циліндром тощо.
Диференціюючи вираз (10.13), дістанем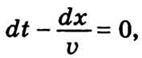о 
або
Де υ – швидкість поширення хвилі. Покажемо тепер, що рівняння хвилі (10.7) задовольняє диференціальне рівняння (10.6) і є його розв’язком. Для цього, диференціюючи вираз (10.7), знайдемо другі частинні похідні від Е по t і х. Вони матимуть такі значення:
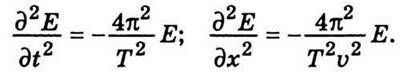
Знайдемо з обох виразів значення Е і прирівняємо їх. Тоді перетворень дістанемо
Прирівнявши рівняння (10.6) і (10.15), неважко дістати вираз для швидкості поширення електромагнітної хвилі
Швидкість поширення світла у вакуумі
Швидкість поширення електромагнітного поля в середовищі дорівнює швидкості світла у вакуумі
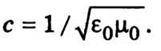
Отже, швидкість поширення електромагнітного поля в середовищі дорівнює швидкості світла у вакуумі, поділеній на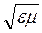 
, де ε і μ відповідно відносна діелектрична і магнітна проникності середовища. Якщо електромагнітна хвиля поширюється у вакуумі, де ε = 1, μ = 1, то υ = с = 2,998 ∙ 108 м/с.
Звідси випливає, що швидкість поширення світла і швидкість поширення електромагнітних хвиль у вакуумі однакові. Це дало підставу Дж. Максвеллу ототожнити світлові хвилі з електромагнітними. Так виникла електромагнітна теорія світла, згідно з якою світлові хвилі є електромагнітними хвилями дуже короткої довжини. Для неферомагнітних речовин μ =1, отже, υ = с /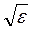 
або
Де n – абсолютний показник заломлення неферомагнітних речовин, тобто показник заломлення відносно вакууму. Згідно із співвідношенням (10.17) показник заломлення для них дорівнює квадратному кореню з діелектричної проникності. Це положення називають законом Максвелла.
До електромагнітних хвиль належать хвилі різної довжини від радіохвиль до гамма-випромінювання. Встановити які-небудь чіткі межі між різними видами електромагнітних випромінювань немає можливості, їх насправді не існує. Тому поділ електромагнітного спектра на певні ділянки має умовний характер, за винятком ділянки, що відповідає видимому випромінюванню, межі якого чітко визначені властивостями людського ока. В табл. 10.1 наведено діапазони, на які умовно поділяють шкалу електромагнітних хвиль.
Таблиця 10.1
Види хвиль | Довжина хвилі, м | Частота, Гц |
Низькочастотні Радіохвилі Ультрарадіохвилі Інфрачервоне випромінювання Видиме світлове випромінювання Ультрафіолетове випромінювання Рентгенівське випромінювання Гамма-випромінювання |
|
|
(1 votes, average: 5.00 out of 5)
Loading...