Функція. Область визначення і область значень функції. Способи задання функцій. Функціональна залежність між величинами як математична модель
Розділ 2. ФУНКЦІЇ
& 19. Функція. Область визначення і область значень функції. Способи задання функцій. Функціональна залежність між величинами як математична модель
У житті ми часто стикаємося із залежностями між різними величинами. Наприклад, периметр квадрата залежить від довжини його сторони, площа прямокутника від його вимірів, маса шматка крейди – від його об’єму, відстань, яку долає рухомий об’єкт, від його швидкості та часу руху тощо.
Щоб розв’язати задачу практичного змісту, доцільно спочатку створити її математичну
Розглянемо приклади залежностей між двома величинами.
Приклад 1. Нехай сторона квадрата дорівнює а см, а його периметр дорівнює Р см. Для кожного значення змінної а можна знайти відповідне значення змінної Р. Наприклад,
Якщо а = 5, то Р = 4 ∙ 5 = 20;
Якщо а = 8, то Р = 4 ∙ 8 = 32;
Якщо а = 1,2, то Р = 4 ∙ 1,2 = 4,8.
Тобто периметр квадрата залежить від довжини його сторони. Математичну модель цієї залежності можна записати формулою Р = 4а.
Оскільки кожному значенню довжини
Змінну а, значення якої вибирають довільно, називають незалежною змінною, а змінну Р, кожне значення якої залежить від вибраного значення а, – залежною змінною.
Приклад 2. Нехай автомобіль рухається з постійною швидкістю 80 км/год. Відстань, яку він при цьому подолає, залежить від часу ного руху.
Позначимо час руху автомобіля (у годинах) буквою t, а відстань, що він подолав (у кілометрах), буквою s. Для кожного значення змінної t (де t > 0) можна знайти відповідне значення s. Наприклад,
Якщо t = 1,5, то s = 80 ∙ 1,5 = 120;
Якщо t = 3, то s = 80 ∙ 3 = 240;
Якщо t = 4,5, то s = 80 ∙ 4,5 = 360.
Залежність змінної s від змінної t можна записати формулою s = 80 t, де t є незалежною змінною, a s – залежною змінною.
У математиці, як правило, незалежну змінну позначають буквою х, а залежну змінну – буквою у. У прикладах, які ми розглянули, кожномузначенню незалежної змінної відповідає лише одне значення залежної змінної.
Незалежну змінну ще називають аргументом, а про залежну змінну кажуть, що вона є функцією від цього аргументу. У наших прикладах – периметр квадрата Р є функцією від довжини його сторони а; відстань s, яку подолав автомобіль зі сталою швидкістю, є функцією від часу руху t. Значення залежної змінної називають значенням функції.
Наприклад, областю визначення функції у прикладі 1 є всі додатні числа о (а ≥ 0).
Областю визначення функції у прикладі 2 є всі невід’ємні числа t, тобто t ≥ 0. Область значень функції у прикладі 1 складається з усіх додатних чисел Р, а область значень функції у прикладі 2-з усіх невід’ємних чисел S, тобто s > 0.
Приклад 3. Функцію задано формулою у =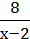 
. Знайти:
1) область визначення функції;
2) значення функції, яке відповідає значенню аргументу, що дорівнює -2; 6; 10;
3) значення аргументу, при якому значення функції дорівнює -1.
Р о з в ‘ я з а н н я. 1) Областю визначення функції є всі такі значення х, при яких дріб 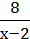має зміст. Знаменник дробу дорівнює нулю при х = 2. Отже, областю визначення функції є всі числа, крім числа 2.
2) Якщо х = -2, то у =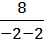 
= – 2; якщо х = 6, то у = 
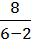= 2; якщо х = 10, то у = 
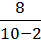= 1.
3) Щоб знайти х, при якому у = -1, треба підставити у формулу функції замість у число -1. Матимемо рівняння:
-1 = 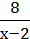, коренем якого є число -6. Отже, значення у = -1 функція набуває при х = -6.
Задавати функцію можна різними способами. У прикладах, які ми розглянули, функції задано формулами: Р = 4а; s = 80t; у =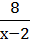 
. Такий спосіб задання функції є досить зручним, бо дає змогу для довільного значення аргументу знаходити відповідне значення функції, та компактним, оскільки в більшості випадків формула мас короткий запис.
Трапляються й функції, які для різних значень аргументу задаються різними формулами. Розглянемо таку функцію та її запис.
Приклад 4. Нехай дано функцію
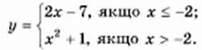
Цей запис означає, що для значень аргументу х ≤ -2, значення функції обчислюються за формулою у – 2х – 7, а для значень аргументу х ≥ -2 – за формулою у = х2 + 1.
Наприклад,
Якщо х = -3, то у = 2 ∙ (-3) – 7 = -13;
Якщо х = -2, то у = 2 ∙ (-2) – 7 = -11;
Якщо х = 0, то у = 02 + 1 = 1;
Якщо х = 5, то у = 52 + 1 = 26.
Задавати функцію можна і таблицею. Такий спосіб задання функції називають табличним. Розглянемо його на прикладі.
Приклад 5. Щогодини, починаючи з восьмої і до тринадцятої, вимірювали атмосферний тиск і одержані дані заносили в таблицю:
Час t, год | 8 | 9 | 10 | 11 | 12 | 13 |
Атмосферний тиск р, мм. рт. ст. | 753 | 754 | 756 | 754 | 753 | 752 |
Таблиця задає відповідність між часом вимірювання t і атмосферним тиском р. Ця відповідність є функцією, бо кожному значенню змінної і відповідає єдине значення змінної р. У цьому прикладі t є незалежною змінною, а р – залежною змінною. Область визначення функції складається із чисел 8; 9; 10; 11; 12; 13 (перший рядок таблиці), а область значень – із чисел 752; 753; 754; 756 (другий рядок таблиці).
Табличний спосіб задання функції зручний тим, що для знаходження значень функції не треба нічого обчислювати. Незручним є те, що таблиця, як правило, займає багато місця і може не містити саме того значення аргументу, яке нас цікавить, наприклад, якщо в першому рядку таблиці такого значення немає. Зокрема, у прикладі 5 неможливо знайти значения функції, що відповідає значенню аргументу, яке дорівнює, наприклад, 8,5 або 14.
Задавати функцію можна також висловленням. Такий спосіб задання функції називають описовим або словесним.
Приклад 6. Кожному натуральному числу поставимо у відповідність квадрат цього числа. Одержимо функцію, область визначення якої складається з усіх натуральних чисел, а область значень – з квадратів цих чисел.
Функціональні залежності, які ми розглянули у прикладах 2 і 5 є математичними моделями реальних процесів: модель руху автомобіля зі сталою швидкістю, модель вимірювання тиску протягом деякого часу.
У подальшому під час вивчення алгебри ми будемо неодноразово звертатися до математичних моделей реальних процесів.
А ще раніше…
Функція – одне з найважливіших понять сучасної математики. Залежності між різними величинами цікавили й стародавніх математиків. Зокрема, у Вавилоні було складено таблиці квадратів і кубів чисел, таблиці сум і добутків двох чисел, у Греції – знайдено співвідношення між елементами кола. У працях І. Ньютона, Р. Декарта, Г. Лейбніца, П. Ферма розглядалося багато функціональних залежностей, пов’язаних з геометрією та фізикою. Так, французькі математики П’єр Ферма (1601-1665) та Рене Декарт (1596-1650) розглядали функцію як залежність ординати точки кривої від її абсциси. Рене Декарт використовував поняття змінної величини. Термін “функція” (від латинського functio – виконання, звершення) для назви залежностей вперше ввів Готфрід Лейбніц (1646-1716). Він пов’язував функцію з графіками Швейцарські математики Йоганн Бернуллі (1667-1748) та його видатний учень Леонард Ейлер (1707- 1783) розглядали функцію як аналітичний вираз, тобто вираз, утворений із змінних і чисел за допомогою тих чи інших аналітичних операцій (дій). Поняття функції як залежності однієї змінної від іншої ввів чеський математик Бернард Больцано (1781-1848), а узагальнив – німецький математик Петер Густав Діріхле (1805-1859).
Найзагальніше сучасне означення функції було запропоноване в середині XX ст. Свій внесок у становлення цього поняття за радянських часів зробили математики М. Гюнтер, І. Гельфанд. С. Соболев, Г. Шилов.
Наведіть приклади функціональної залежності однієї змінної від іншої, назвіть в них незалежну змінну і залежну. Що називають функцією? Що називають областю визначення функції і що областю значень функції? Які є способи задання функції? Наведіть приклад функції, заданої формулою. Наведіть приклад функціональної залежності між величинами, що є математичною моделлю реальних процесів.
708. (Усно) Чи залежить периметр рівностороннього трикутника від довжини його сторони? Чи є периметр цього трикутника функцією від довжини сторони трикутника? Якщо так, то задайте цю функцію формулою за умови, що сторона трикутника дорівнює а.
709. (Усно) Які з даних формул задають функцію? Укажіть для них незалежну змінну (аргумент) та залежну змінну:
1) a = 56 – 7;
2) m = n2 + n + m3;
3) у =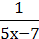
;
4) 
+ 
– 2 = 0;
5) р = t2 + t – 5;
6) abc = 4.
710. (Усно) Які з даних формул задають функцію? Укажіть для них незалежну змінну (аргумент) та залежну змінну:
1) m = 2n2 – 5;
2) у = x3 – х2 + 3;
3) ab + а2 + b2 = 0;
4) х + у = ху;
5) d =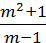 
;
6) р2m3 =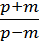 
.
711. (Усно) Площу круга знаходять за формулою S = пr2, де r – радіус круга. Чи задає ця формула функцію? Якщо так, укажіть її аргумент та область визначення.
712. Площа прямокутника зі сторонами х см і 10 см дорівнює S. Виразіть формулою залежність S від х. Чи задає ця формула функцію?
713. Об’єм куба з ребром а см дорівнює V см3. Виразіть формулою залежність V від а. Чи задає ця формула функцію? Знайдіть за цією формулою значення V, якщо:
1) а = 5;
2) а = 7;
3) а = 
.
714. Периметр прямокутника зі сторонами х дм і 8 дм дорівнює Р дм. Запишіть формулу залежності Р від х. Для значень аргументу х = 2; 4; 5; 15 знайдіть відповідні значення функції Р.
715. (Усно) Функцію задано формулою у = -2х.
1) Яка змінна с незалежною, а яка залежною?
2) Знайдіть значення функції, що відповідають значенням аргументу 3; 0; 8.
716. Обчисліть значення функції, заданої формулою у = 5х – 7 для значень аргументу, що дорівнюють -2; 0; 5; 10.
717. Знайдіть значення функції, заданої формулою у =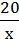 
, для значень аргументу, що дорівнюють 40; -10; 4; 5.
718. Функцію задано формулою у = – 
. У таблиці наведено значення її аргументу. Заповніть таку таблицю в зошиті, обчисливши відповідні значення функції:
Х | -12 | -6 | -5 | -3 | 2 | 4 | 8 | 10 |
У |
719. Функцію задано формулою у = 4х + 3. У таблиці наведено значення її аргументу. Заповніть таку таблицю в зошиті, обчисливши відповідні значення функції:
Х | -7 | -5 | -3 | -1 | 2 | 4 | 6 | 8 |
У |
720. Складіть таблицю значень функції, заданої формулою у = х2 – 3, для значень аргументу -3; -2; -1; 0; 1; 2.
721. Складіть таблицю значень функції, заданої формулою у = 5 – х?, для значень аргументу -2; -1; 0; 1; 2; 3.
722. Потяг, рухаючись зі швидкістю 65 км/год, проходить за t год відстань s км. Задайте формулою залежність s від t. Обчисліть значення функції, які відповідають значенням аргументу, що дорівнюють 1; 2,4; 3; 5,8.
723. Кожному натуральному значенню n відповідає втричі більше за нього число N. Задайте формулою залежність N від n. Знайдіть значення функції, що відповідають значенням аргументу 2; 7; 13; 20.
724. Знайдіть область визначення функції:
1) y = 2x – 7;
2) y =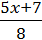 
;
3) y =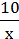 
;
4) y =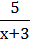 
.
725. Знайдіть область визначення функції:
1) y = 3x + 8;
2) y =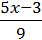 
;
3) y = –
;
4) y =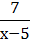 
.
726. Знайдіть значення аргументу, при якому:
1) функція у = -3х набуває значення -6; 9; 15;
2) функція у = 5х – 1 набуває значення -1; 4; 14.
727. Знайдіть значення аргументу, при якому:
1) функція у = 4х набуває значення -8; 0; 12;
2) функція у = 4х + 3 набуває значення -1; 3; 17.
728. Функцію задано таблицею:
Х | -2 | -1 | 0 | 1 | 2 |
У | -5 | -3 | -1 | 2 | 7 |
Знайдіть:
1) значення функції, якщо х = -2; 0; 1;
2) значення аргументу, при якому значення функції дорівнює -3; 2; 7;
3) область визначення функції;
4) область значень функції.
729. Функцію задано таблицею:
Х | 1 | 2 | 3 | 4 | 5 |
У | -2 | 0 | 2 | 5 | 7 |
Знайдіть:
1) значення функції, яке відповідає значенню аргументу, що дорівнює 1; 3; 4;
2) значення аргументу, при якому у = 0; 5; 7;
3) область визначення функції;
4) область значень функції.
730. Функцію задано формулою у = Х. Заповніть порожні комірки таблиці:
Х | -8 | 1,6 | 20,8 | |
У | -9 | – | 1 | 20,7 |
731. Функцію задано формулою у = 
х. Заповніть порожні комірки таблиці:
Х | -10 | 0 | 8,5 |
У | -1,2 | – | 13,5 |
732. Знайдіть область визначення функції, заданої формулою:
1) y =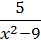 
;
2) y =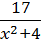 
;
3) y =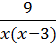 
;
4) y =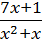 
;
5) y =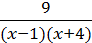 
;
6) y =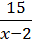 
+ 
.
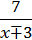733. Знайдіть область визначення функції:
1) y =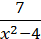 
;
2) y =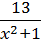 
;
3) y =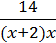 
;
4) y =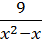 
;
5) y =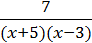 
;
6) y =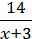 
+ 
.
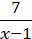734. На початку нагрівання вода мала температуру 20 °С. При нагріванні температура води щохвилини підвищувалася на 5 °С.
1) Задайте формулою залежність температури води Т від часу t її нагрівання.
2) Знайдіть значення Т, що відповідає значенню аргументу t = 7; 9; 10.
3) Знайдіть значення t, яким відповідає Т = 45; 60; 70.
4) Знайдіть значення t, при якому вода закипить?
735. Від’їхавши на відстань 10 км від міста, велосипедист зупинився. А через деякий час продовжив рух зі швидкістю 15 км/год.
1) Задайте формулою залежність відстані s (у км), яку подолав велосипедист, від часу t (у год), що відраховується після зупинки.
2) Знайдіть значення s, що відповідає значенню аргументу t = 1; t = 2; t = 5.
3) Знайдіть значення t, яким відповідає s = 34; s = 55; s = 70.
736. У таблиці подано залежність функції у від аргументу х.
Х | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
У | -3 | -2 | 1 | -3 | 5 | 1 | 6 | -2 | -3 |
Знайдіть:
1) значення у, якщо х = -4; -1; 0; 3;
2) значення х, яким відповідає у = -3; -2; 5;
3) значення х, якому відповідає таке саме значення у;
4) область визначення функції;
5) область значень функції.
737. У таблиці подано залежність функції у від аргументу х.
Х | -8 | -6 | -4 | -2 | 0 | 2 | 4 | 6 | 8 |
У | -1 | 2 | 4 | 2 | 4 | 7 | 2 | -1 | 9 |
Знайдіть:
1) значення у, якщо х = – 8; -2; 4; 6;
2) значення х, яким відповідає у = -1; 4; 7;
3) значення х, якому відповідає протилежне до х значення у;
4) область визначення функції;
5) область значень функції.
738. Складіть таблицю значень функції у = 0,6 – 0,3х, де -2 ≤ х ≤ 5, з кроком, що дорівнює 1. Використовуючи цю таблицю, укажіть:
1) значення функції, яке відповідає значенню аргументу, що дорівнює 0;
2) значення аргументу, при якому значення функції дорівнює 0.
739. Знайдіть значення функції для х = -5; х = 0; х = 3, якщо:
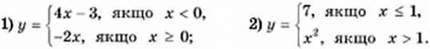
740. Знайдіть значення функції для значення аргументу, яке дорівнює -2: 0: 4, якщо:
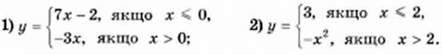
741. Знайдіть найменше значення функції у = х2 + 2х + 5.
Вправи для повторення
742. Обчисліть:
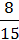∙ 0,5625 – (
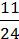+ 1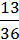 
) ∙ 1,44 + 2 
.
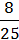743. Якими одночленами треба заповнити комірки, щоб рівність перетворилася на тотожність:
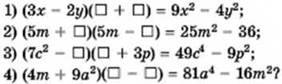
744. Сторона квадрата па 4 см більша за одну сторону прямокутника і на 5 см менша за другу. Знайдіть сторону квадрата, якщо його площа на 10 см2 більша за площу прямокутника.
Цікаві задачі для учнів неледачих
745. У трьох коробках лежать кульки: у першій дві білого кольору, у другій – дві чорного кольору, у третій – білого й чорного. На коробках є таблички з написами, що відповідають кольору кульок: БВ, ЧЧ і БЧ, але вміст жодної з коробок не відповідає її табличці. Як, взявши з якоїсь однієї коробки навмання одну кульку, визначити колір кульок, що лежать у кожній з коробок?
(1 votes, average: 5.00 out of 5)
Loading...