Функція. Область визначення та область значень функції
Урок № 61
Тема. Функція. Область визначення та область значень функції
Мета: вдосконалювати та поглиблювати вміння та навички розв’язувати основні види завдань для функції, заданої формулою.
Тип уроку: застосування знань.
Хід уроку
I. Організаційний момент
II. Перевірка домашнього завдання
1) № 1,2 перевіряємо, зібравши зошити, № 2 бажано розібрати (навести приклади і сформулювати основну ідею, найбільш вдалі роботи можна оцінити).
2) № 3 (випереджальне домашнє завдання) розбираємо ретельно, бо ці вправи є основою
Завдання 1. Поясніть хід розв’язання рівнянь:
1) х2 – 2х + 1 = 0;
2) х2 – 2х = 0;
3) х2 + 1 = 0,
4) |х – 3| = 0;
5) |х – 3| + 1 = 0.
Які корені мають рівняння? Що це означає?
Завдання 2. Поясніть, як, використавши результати завдання 1, знайти значення змінної х, при яких виконуються нерівності:
1) х2 – 2х + 1 ? 0;
2) х2 – 2х? 0;
3) х2 + 1 ? 0;
4) |х – 3| ? 0;
5) |х – 3| + 1 ? 0.
Висновок. Бажано, щоб учні усвідомили, що розв’язки нерівності вигляду f(х) ? 0 можна знайти, розв’язавши рівняння f(х) = 0 і виключивши із множини всіх (раціональних)
III. Формулювання мети й завдань уроку
@ Основна мета уроку – вдосконалити вміння та навички знаходження за формулою значення функції, а також поглибити ці вміння, розв’язавши задачі високого рівня.
IV. Актуалізація опорних знань
Виконання усних вправ
1. Укажіть область визначення функції, яку задано формулою:
1) у = 2х; 2) у = 3х + 4; 3)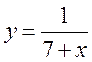 
.
2. Знайдіть значення функції, яку задано формулою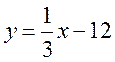 
, що відповідає значенню аргументу: -6; 12; 0; 1,5.
3. Функцію задано формулою: 1) у = 1,3х; 2)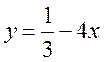 
.
Знайдіть значення аргументу, якому відповідає значення функції, що дорівнює 0.
V. Удосконалення та поглиблення знань, умінь
@ На цьому уроці, коли основні поняття, пов’язані з поняттям функції, вже засвоєні і базові вміння щодо розв’язування основних задач для функції сформовані, основну увагу приділяємо розв’язуванню завдань достатнього і високого рівнів, які б поєднували новий матеріал із вивченим раніше матеріалом. Якщо рівень підготовки учнів досить високий, можна розширити знання учнів, ознайомивши їх із кусковим способом задання функції.
Виконання письмових вправ
1. Знайдіть область визначення функції, заданої формулою:
1) 
;
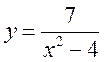2) 
;
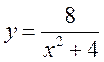3) 
;
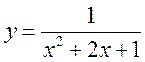4) 
;
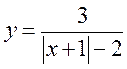5*)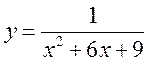 
.
2*. Функція задана кусково:
1) 
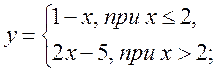2) 
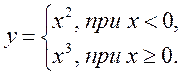
Знайдіть значення функції, що відповідає значенню аргументу, що дорівнює -2; 0; 3.
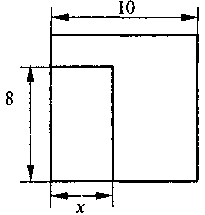
3. Від квадрата зі стороною 10 см відрізали прямокутник зі сторонами 8 см і х см (див. рис.). Позначивши площу частини, що залишилась (у см2), буквою у, виразіть залежність у від х формулою. Знайдіть:
1) значення у, якщо х = 2,5;
2) значення х, при якому у = 20; 36;
3) область визначення цієї функції.
4*. Знайдіть найменше значення функції у = х2 – 4х + 2.
5*. Доведіть, що функція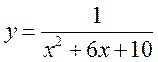 
не може набувати від’ємних значень. Яка область визначення функції? Якого найбільшого значення набуває функція?
6*. Додатково (на повторення). Встановіть пропущене число.
Ху + 3х2 |
| 5 |
Х3 – 2у |
| ? |
VI. Підсумок уроку
Контрольні запитання
1. Наведіть приклад функціональної відповідності між числами.
2. Поясніть на прикладі, що таке аргумент і що таке функція.
3. Які ви знаєте способи задання функції?
4. Що називають областю визначення та областю значень функції?
VII. Домашнє завдання
Повторіть зміст основних понять теми (див. контрольні запитання).
№ 1. Функцію задано формулою у = 5х – 3.
1) Знайдіть значення функції, які відповідають значенням аргументу -8; 0; 16.
2) Знайдіть значення аргументу, якому відповідає значення функції: -3; 1.
3) При якому значенні означення функції дорівнює значенню аргументу? в 3 рази більше за значення аргументу?
№ 2. Розгляньте функцію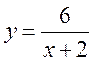 
, де -1 ? х? 4. Знайдіть пари значень х та у для всіх цілих значень х та запишіть їх у вигляді (х; у). Як можна зобразити ці пари чисел?
Виконайте відповідну побудову.
(1 votes, average: 5.00 out of 5)
Loading...