Гармонічні коливання
ЕЛЕКТРОДИНАМІКА
2-й семестр
Коливання й хвилі
УРОК 2/24
Тема. Гармонічні коливання
Мета уроку: ознайомити учнів з поняттям гармонічних коливань.
Тип уроку: урок вивчення нового матеріалу.
ПЛАН УРОКУ
Контроль знань | 5 хв. | 1. Механічні коливання. 2. Основні характеристики коливань. 3. Вільні коливання. Умови виникнення вільних коливань |
Демонстрації | 5 хв. | 1. Вільні коливання вантажу на пружині. 2. Запис коливального |
Вивчення нового матеріалу | 25 хв. | 1. Рівняння коливального руху вантажу на пружині. 2. Гармонічні коливання |
Закріплення вивченого матеріалу | 10 хв. | 1. Якісні питання. 2. Навчаємося розв’язувати задачі |
ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ
1. Рівняння коливального руху вантажу на пружині
У багатьох коливальних системах за малих відхилень від положення рівноваги модуль обертальної сили, а значить, і модуль прискорення прямо пропорційний модулю зсуву щодо положення рівноваги.
Покажемо, що в такому випадку зсув залежить від
Якщо вантаж масою m зміщений від положення рівноваги на величину х (для положення рівноваги х = 0), то на нього діє сила пружності Fx = – kx, де k – твердість пружини (знак “-” означає, що сила в будь-який момент часу напрямлена у бік, протилежний зсуву).
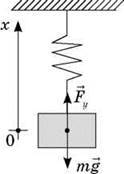
Відповідно до другого закону Ньютона Fx = mах. Таким чином, рівняння, що описує рух вантажу, має вигляд:
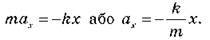
Позначимо?2 = k/m. Тоді рівняння руху вантажу буде мати вигляд:
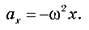
Рівняння такого виду називається диференціальним рівнянням. Розв’язком цього рівняння є функція:
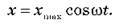
Таким чином, за вертикального зсуву вантажу на пружині від положення рівноваги він буде робити вільні коливання. Координата центра мас при цьому змінюється за законом косинуса.
2. Гармонічні коливання
Переконатися в тому, що коливання відбуваються за законом косинуса (або синуса) можна на досліді. Учням доцільно показати запис коливального руху (див. рисунок).
O Коливання, за яких зсув залежить від часу за законом косинуса (або синуса), називаються гармонічними.
Вільні коливання вантажу на пружині являють приклад механічних гармонічних коливань.
Нехай у деякий момент часу t1 координата коливного вантажу дорівнює x1 = xmax cos? t1. Відповідно до визначення періоду коливань, у момент часу t2 = t1 + T координата тіла повинна бути такою самою, як і в момент часу t1, тобто х2 = х1:
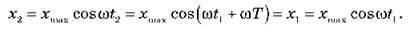
Період функції cos? t дорівнює 2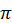
, отже, ?Т = 2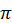, або
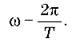
Але оскільки Т = 1/v, то? = 2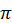V, тобто циклічною частота коливань? є кількість повних коливань, здійснених за 2 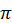секунд.
ПИТАННЯ ДО УЧНІВ У ХОДІ ВИКЛАДУ НОВОГО МАТЕРІАЛУ
Перший рівень
1. Наведіть приклади гармонічних коливань.
2. Тіло виконує незатухаючі коливання. Які з величин, що характеризують цей рух, постійні, а які змінюються?
Другий рівень
Як змінюються сила, що діє на тіло, його прискорення й швидкість під час здійснення ним гармонічних коливань?
ЗАКРІПЛЕННЯ ВИВЧЕНОГО МАТЕРІАЛУ
Навчаємося розв’язувати задачі
1. Напишіть рівняння гармонічного коливання, якщо його амплітуда 0,5 м, а частота 25 Гц.
2. Коливання вантажу на пружині описують рівнянням х = 0,1sin0,5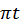
. Визначте амплітуду, період, колову частоту й частоту коливань.
3. Амплітуда коливання 2 см, зміщення 1 см. Скільки часу минуло від початку коливань?
Розв’язання
Якби рух був рівномірним, то відповідь була б: t = 1/8Т. Але рух вантажу в цьому завданні нерівномірний. Рівняння руху має вигляд: 1 = 2cos? t, звідки cos? t = 1/2. Отже, ?t = 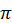/3, звідки 
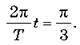Таким чином, t = 1/6Т.
4. Коливання описують формулою х = 0,12sin20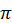T. Знайдіть амплітуду, частоту й період коливань.
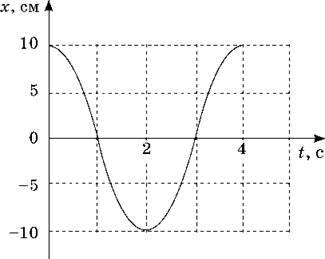
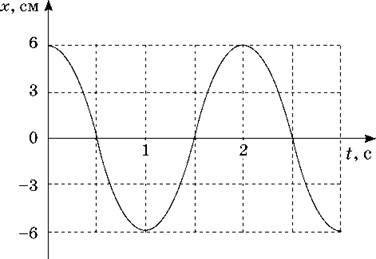
5. На рисунку наведений графік гармонічного коливання. Знайдіть амплітуду, частоту й період коливання. Запишіть формулу залежності x(t).
ЩО МИ ДІЗНАЛИСЯ НА УРОЦІ
– Коливання, під час яких зміщення залежить від часу за законом косинуса (або синуса), називаються гармонічними.
– Рівняння гармонічних коливань:
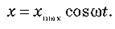
– Циклічною частотою коливань? є кількість повних коливань, здійснюваних за 2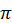 секунд.
Домашнє завдання
1. Підр.: § 19.
2. 3б.:
Рів1 № 10.4; 10.19.
Рів2 № 10.32; 10.33; 10.34, 10.35.
(1 votes, average: 5.00 out of 5)
Loading...