Гармонічні коливання математичного й пружинного маятників
ЕЛЕКТРОДИНАМІКА
2-й семестр
Коливання й хвилі
УРОК 3/25
Тема. Гармонічні коливання математичного й пружинного маятників
Мета уроку: ознайомити учнів із законами коливань математичного й пружинного маятників.
Тип уроку: урок вивчення нового матеріалу.
ПЛАН УРОКУ
Контроль знань | 5 хв. | 1. Основні характеристики коливань. 2. Вільні коливання. Умови виникнення вільних коливань. 3. Гармонічні коливання |
Демонстрації | 5 хв. | 1. 2. Вільні коливання пружинного маятника. 3. Залежність періоду коливань математичного маятника від довжини. 4. Залежність періоду коливань вантажу на пружині від пружних властивостей пружини й маси вантажу |
Вивчення нового матеріалу | 25 хв. | 1. Математичний маятник. 2. Пружинний маятник |
Закріплення вивченого матеріалу | 10 хв. | 1. Якісні питання. 2. Навчаємося розв’язувати задачі |
ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ
1. Математичний маятник
Щоб знайти період коливань вантажу, підвішеного
O Математичним маятником називається ідеалізована коливальна система без тертя, що складає з невагомої й нерозтяжної нитки, на якій підвішена матеріальна точка.
Розрахунки показують, що
O період коливань математичного маятника дорівнює:
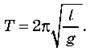
Ми можемо на дослідах переконатися, що період коливань математичного маятника не залежить від маси вантажу й визначають його тільки довжиною нитки.
Оскільки період коливань математичного маятника залежить від прискорення вільного падіння g, то за допомогою маятника можна робити точні виміри g.
Відомо, що в різних точках земної кулі прискорення вільного падіння різне. Воно залежить не тільки від форми Землі, але й від наявності в її надрах важких (метали) або легких (газ, нафта) речовин. Отже, виходить, що і період коливань маятника в різних точках буде різний. Цю властивість використовують, зокрема, для визначення покладів корисних копалин.
Формула періоду коливань математичного маятника вперше була встановлена голландським ученим Християном Гюйгенсом. Одержавши цю формулу, Гюйгенс тим самим довів, що малі коливання маятника відбуваються з періодом, що не залежить від їхньої амплітуди. Використовуючи цю властивість і назвавши її ізохронністю маятника, Гюйгенс 1657 року сконструював перші маятникові годинники.
2. Пружинний маятник
Підвішуючи до пружини вантажі різної маси, можна помітити, що відповідно до збільшення маси в 4 рази період коливань збільшується в 2 рази. А якщо той самий вантаж підвішувати до пружин різної твердості, то можна помітити, що зі збільшенням твердості пружини зменшується період коливань маятника.
Розрахунки показують, що
O період малих коливань пружинного маятника дорівнює:
Відзначимо, що як для пружинного, так і для математичного маятників період коливань не залежить від амплітуди. Це важлива загальна властивість гармонічних коливань. Її використовують, наприклад, у механічних годинниках.
На відміну від маятникових годин, пружинні годинники можна зробити настільки малими, що їх можна носити на руці.
ПИТАННЯ ДО УЧНІВ У ХОДІ ВИКЛАДУ НОВОГО МАТЕРІАЛУ
Перший рівень
1. Наведіть приклади фізичного, нитяного й пружинного маятників.
2. Як зміниться період коливань математичного маятника, якщо масу вантажу збільшити (зменшити)?
3. Назвіть причини вільних коливань математичного маятника.
4. Назвіть причини вільних коливань пружинного маятника.
Другий рівень
1. За якої умови коливання математичного маятника можна вважати гармонічними?
2. Як зміниться період коливань пружинного маятника, якщо амплітуду коливань зменшити у два рази?
3. Що спільного у вільних коливаннях математичного й пружинного маятників?
ЗАКРІПЛЕННЯ ВИВЧЕНОГО МАТЕРІАЛУ
1). Якісні питання
1. Коли період коливань математичного маятника більший: узимку або влітку?
2. Підвішений на пружині вантаж, перебуваючи в рівновазі, розтягує пружину на 10 см. Чи вистачить цих даних, щоб знайти період коливань вантажу на пружині?
3. Як змінився хід маятникових годин, привезених з Києва на наукову станцію в Антарктиді?
2). Навчаємося розв’язувати задачі
1. Коли до пружини підвісили вантаж, вона розтяглася на 20 см. Вантаж відвели вниз і відпустили. Який період Т коливань, що виникли?
2. Сталева кулька, підвішена до пружини, здійснює вертикальні коливання. Як зміниться період коливань, якщо до пружини підвісити мідну кульку того ж радіуса? (Відповідь: зменшиться в 1,07 рази.)
3. Яке відношення довжин двох математичних маятників, якщо один з них робить 31 коливання за той самий час, за який другий виконує 20 коливань? (Відповідь: довжина другого маятника більше у 2,4 рази.)
ЩО МИ ДІЗНАЛИСЯ НА УРОЦІ
– Математичним маятником називається ідеалізована коливальна система без тертя, що складається з невагомої й нерозтяжної нитки, на якій підвішена матеріальна точка.
– Період коливань математичного маятника дорівнює:
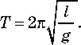
– Період малих коливань пружинного маятника дорівнює:
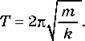
Домашнє завдання
1. Підр.: § 19.
2. 3б.:
Рів1 № 10.5; 10.8; 10.20; 10.21.
Рів2 № 10.36; 10.37; 10.38; 10.39.