Головна ⇒ 📌Довідник з геометрії ⇒ Геометричне місце точок
Геометричне місце точок
Геометрія
Основні властивості найпростіших геометричних фігур
Геометричне місце точок
Геометричним місцем точок (ГМТ), які мають певну властивість, називається така фігура, що складається з усіх точок площини, які мають цю властивість, і тільки з них.
Довести, що фігура М є ГМТ, які мають властивість Р, означає довести два такі твердження.
1. Якщо точка А ∈ М, то вона має властивість Р.
2. Якщо точка А має властивість Р, то А є М.
Приклади
1) Коло – це ГМТ, рівновіддалених від даної точки.
2) Бісектриса кута – це ГМТ, рівновіддалених від сторін кута (див. рисунок):
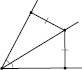
3. Серединний перпендикуляр до відрізка – це ГМТ, рівновіддалених від кінців відрізка (див. рисунок):
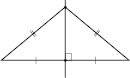
Related posts:
- ГЕОМЕТРИЧНЕ МІСЦЕ ТОЧОК РОЗДІЛ 4 КОЛО І КРУГ. ГЕОМЕТРИЧНІ ПОБУДОВИ & 19. ГЕОМЕТРИЧНЕ МІСЦЕ ТОЧОК Щоб розв’язувати складніші задачі на побудову, потрібно знати, що таке геометричне місце точок. Геометричним місцем точок (ГМТ) називають фігуру, яка складається з усіх точок, що мають певну властивість. Розглянемо кілька геометричних місць точок площини. Коло – геометричне місце точок, рівновіддалених від даної точки. […]...
- Геометричне місце точок Урок № 47 Тема. Геометричне місце точок Мета: – сформувати в учнів уявлення про зміст поняття “геометричне місце точок”, властивість і ознаку точок, що належать ГМТ ; – сформувати знання змісту та схеми доведення теореми про ГМТ. Сформувати вміння: – відтворювати означення властивості та ознаки ГМТ, теорем про ГМТ; – використовувати ці твердження під час […]...
- Коло Геометрія Основні властивості найпростіших геометричних фігур Коло Колом називається фігура, яка складається з усіх точок площини, рівновіддалених від даної точки. Ця точка називається Центром кола. Відстань від точок кола до його центра називається Радіусом кола. Радіусом також називається будь-який відрізок, що сполучає точку кола з його центром. Відрізок, що сполучає дві точки кола, називається Хордою. […]...
- Симетрія відносно точки Геометрія Рух Симетрія відносно точки Нехай O – фіксована точка, X – довільна точка площини. Відкладемо на продовженні відрізка OX за точку O відрізок , що дорівнює OX. Точка називається Симетричною точці X відносно точки O (див. рисунок). Очевидно, що точка, симетрична , є точка X. Перетворення фігури F у фігуру , при якому кожна […]...
- Вступ. Точка і пряма. Властивості точок і прямих Урок № 1 Тема. Вступ. Точка і пряма. Властивості точок і прямих Мета: ознайомити учнiв з предметом вивчення геометрiї, планiметрiї та iз поняттям найпростiших фiгур у геометрiї, домагатися вiд учнів свiдомого засвоєння термiнологiї, що описує взаємне розташування точок та прямих на площинi, формулювання основних властивостей розташування точок та прямих; виробити первиннi вмiння позначати точки та […]...
- ПОЗНАЧЕННЯ ТОЧОК, ВІДРІЗКІВ ЛІТЕРАМИ ЛАТИНСЬКОГО АЛФАВІТУ. ПОРІВНЯННЯ ДОВЖИН ВІДРІЗКІВ ОЗНАКИ І ВЛАСТИВОСТІ ПРЕДМЕТІВ. МНОЖИНИ. ГЕОМЕТРИЧНІ ФІГУРИ. НАТУРАЛЬНІ ЧИСЛА 1-10 І ЧИСЛО 0 Урок 28. ПОЗНАЧЕННЯ ТОЧОК, ВІДРІЗКІВ ЛІТЕРАМИ ЛАТИНСЬКОГО АЛФАВІТУ. ПОРІВНЯННЯ ДОВЖИН ВІДРІЗКІВ Мета: ознайомити учнів з позначенням точок, відрізків літерами латинського алфавіту; вчити порівнювати довжину відрізків на око; розвивати спостережливість; виховувати старанність. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. ПОВТОРЕННЯ ВИВЧЕНОГО МАТЕРІАЛУ 1. Весела […]...
- Відрізок і його довжина § 1. Найпростіші геометричні фігури та їхні властивості 2. Відрізок і його довжина Практичні завдання 20. Точки С, D, Е належать відрізку AB, а точки F, M, K не належать відрізку АВ. 21. Утворилося три відрізки АВ, ВС, АС. 22. Точка С лежить між точками А і В, а точка D – між точками В […]...
- Многогранники Геометрія Многогранники Двогранним кутом називається фігура, утворена двома півплощинами зі спільною прямою, що їх обмежує, – ребром двогранного кута. Півплощини називаються Гранями двогранного кута. Площина, перпендикулярна до ребра двогранного кута, перетинає його грані по двох півпрямих. Кут, утворений такими півпрямими, називається Лінійним кутом двогранного кута (див. рисунок). За міру двогранного кута приймається міра його лінійного […]...
- Вправи 575-624 575. АВ і АС дотикаються до кола з центром О у точках В і С. ∠CBO = 40°. ?АBО – прямокутний, OB ⊥ AB (OB – радіус, проведений в точку дотику). ?АСО – прямокутний (ОС – радіус, проведений в точку дотику). ∠ABO = 90°; ∠ACO = 90°; ?ВОС – рівнобедрений, OB = ОС; ∠OBC = […]...
- Тематичне оцінювання № 5 Урок 52 Тема. Тематичне оцінювання № 5 Мета уроку: перевірити навчальні досягнення учнів з теми “Декартові координати у просторі”. Хід уроку Тематичне оцінювання № 5 можна провести у вигляді тематичної контрольної роботи. 1. Тематична контрольна робота № 5 Варіант А 1. Чи лежать точки А, В, С на одній прямій, якщо А(1;1;-3), В (-1;3;5), С […]...
- Означення. Аксіоми Геометрія Основні властивості найпростіших геометричних фігур Означення. Аксіоми Геометрія – це наука про властивості геометричних фігур. Зверніть увагу: геометрична фігура – це не тільки трикутник, коло, піраміда тощо, а й будь-яка множина точок. Планіметрія – це розділ геометрії, у якому вивчаються фігури на площині. Точка і Пряма є основними поняттями планіметрії. Це означає, що цим […]...
- РОБОТА В ЕЛЕКТРОСТАТИЧНОМУ ПОЛІ. ПОТЕНЦІАЛ ПОЛЯ. РІЗНИЦЯ ПОТЕНЦІАЛІВ ДВОХ ТОЧОК ПОЛЯ Фізика підготовка до ЗНО комплексне видання ЕЛЕКТРОДИНАМІКА 1. ОСНОВИ ЕЛЕКТРОСТАТИКИ 1.5. РОБОТА В ЕЛЕКТРОСТАТИЧНОМУ ПОЛІ. ПОТЕНЦІАЛ ПОЛЯ. РІЗНИЦЯ ПОТЕНЦІАЛІВ ДВОХ ТОЧОК ПОЛЯ Робота в електростатичному полі: – не залежить від шляху, а визначається координатами точок, між якими переноситься заряд; – у будь-якому замкненому контурі дорівнює нулю. Такі поля називаються потенціальними. Потенціал поля (φ) у даній […]...
- Описані і вписані кола Розділ 1. Найпростіші геометричні фігури та їх властивості § 17. Описані і вписані кола 671. Коло, описане навколо трикутника, зображено на мал. 372. 672. Коло, вписане у трикутник, зображено на мал. 375. 673. Центр кола, описаного навколо гострокутного трикутника, лежить всередині трикутника. Центр кола, описаного навколо прямокутного трикутника, лежить на середині гіпотенузи. Центр кола, описаного […]...
- Тригранний і многогранний кути Геометрія Многогранники Тригранний і многогранний кути Нехай промені a, b, c виходять з однієї точки й не лежать в одній площині. Тригранним кутом називається фігура, яка складається з трьох плоских кутів , , (див. рисунок). Ці кути називаються Гранями тригранного кута, а їх сторони – Ребрами. Спільна вершина плоских кутів називається Вершиною тригранного кута. Двогранні […]...
- Перпендикуляр і похила Геометрія Стереометрія Перпендикуляр і похила Перпендикуляром, опущеним із даної точки на дану площину, називається відрізок, що сполучає дану точку з точкою площини й лежить на прямій, перпендикулярній до площини. Кінець цього відрізка, який лежить у площині, називається Основою перпендикуляра. Відстанню від точки до площини називається довжина перпендикуляра, опущеного із цієї точки на площину. На рисунку […]...
- Переміщення та його властивості. Рівні фігури УРОК № 33 Тема. Переміщення та його властивості. Рівні фігури Мета уроку: формування поняття переміщення та рівних фігур; вивчення властивостей переміщення. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур”. Рухи” [13]. Вимоги до рівня підготовки учнів: описують рівність фігур; будують фігури, у які переходять дані фігури при переміщеннях; формулюють властивості переміщення; застосовують вивчені означення […]...
- Відрізки та їх вимірювання Розділ 1. Найпростіші геометричні фігури та їх властивості § 2. Відрізки та їх вимірювання 28. 1) Кінці відрізка MN: М і N; внутрішні точки: А, О, В. 2) Кінці відрізка AN: A i N; внутрішні точки: О i B. 3) Кінці відрізка AB: А і В; внутрішня точка: О. 29. Утворилося три відрізки: AB, АС, […]...
- Найпростіші задачі па побудову Розділ 1. Найпростіші геометричні фігури та їх властивості § 18. Найпростіші задачі па побудову 708. Щоб побудувати трикутник, що дорівнює трикутнику ABC, треба провести три кола радіусами 5 см, 6 см і 9 см. 709. 710. 1) AС = 5 см; 2) AС = 0,35 дм; 3) AС = 43 мм. 711. 1) Будуємо відрізок […]...
- Метод геометричних місць Урок № 48 Тема. Метод геометричних місць Мета: домогтися засвоєння учнями схеми дій, що покладено в основу методу геометричних місць. Сформувати вміння: – відтворювати схему, що лежить в основі методу геометричних місць; – виконувати дії, що передбачені цією схемою. Тип уроку: засвоєння знань, умінь та навичок. Наочність і обладнання: набір демонстраційного креслярського приладдя. ХІД УРОКУ […]...
- Поняття про перетворення фігур УРОК № 32 Тема. Поняття про перетворення фігур Мета уроку: дати уявлення учням про перетворення фігур на площині. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: пояснює, що таке перетворення. Хід уроку І. Перевірка домашнього завдання Перевірити наявність виконаного домашнього завдання та відповісти на запитання, які виникли […]...
- Вправи 625-682 625. Геометричним місцем центрів кіл радіуса R, що проходить через дану точку А, є коло із центром в точці А і радіусом R. 626. Геометричним місцем центрів кіл, що дотикаються до сторін даного нерозгорнутого кута, є бісектриса даного кута без його вершини О. ОК – бісектриса. 627. Геометричним місцем точок С, які є вершинами трикутників […]...
- ПЕРПЕНДИКУЛЯРНІ І ПАРАЛЕЛЬНІ ПРЯМІ РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ & 5. ПЕРПЕНДИКУЛЯРНІ І ПАРАЛЕЛЬНІ ПРЯМІ Пригадайте, як можуть розташовуватися на площині дві прямі. Якщо вони перетинаються, то утворюють чотири кути – дві пари вертикальних кутів. Йдеться про кути, менші від розгорнутого. Менший із цих кутів вважають кутом між даними прямими. Наприклад, на малюнку 56 прямі АВ і […]...
- ВІДРІЗКИ І ЇХ ДОВЖИНИ РОЗДІЛ 1 НАЙПРОСТІШІ ГЕОМЕТРИЧНІ ФІГУРИ ТА ЇХ ВЛАСТИВОСТІ & 2. ВІДРІЗКИ І ЇХ ДОВЖИНИ Дві точки прямої розділяють цю пряму на три частини: два промені і відрізок. Відрізком АВ називають частину прямої, яка складається з точок А і В та всіх точок, що лежать між ними. Точки А і В називають кінцями відрізка АВ. Усі […]...
- Паралельне перенесення в просторі Урок 49 Тема. Паралельне перенесення в просторі Мета уроку: формування знань учнів про паралельне перенесення в просторі; вивчення його властивостей та застосування їх до розв’язування задач. Обладнання: схеми “Відстань між двома точками” (див. урок 46) і “Координати середини відрізка” (див. урок 47), моделі куба і прямокутного паралелепіпеда. Хід уроку І. Перевірка домашнього завдання 1. Перевірити […]...
- Точка та прямі § 1. Найпростіші геометричні фігури та їхні властивості 1. Точка та прямі Практичні завдання 1. 2. Прямі ME, МК, ЕК, EM, КМ, КЕ. 3. Точка С належить прямій а, точка С належить прямій b. 4. Утворилося три прямих. 5. 6. Можна отримати три або одну точку перетину. 7. 1) 2) 3) Вправи 8. 1) Прямій […]...
- Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Візьмемо три взаємно перпендикулярні прямі Oх, Oy, Oz, які перетинаються в одній точці О (див. рисунок). Проведемо через кожну пару цих прямих площину. Площина, яка проходить через прямі Oх і Oу, називається площиною Oxy. Дві інші площини називаються відповідно Oxz і Oyz. Прямі Ox, Oy, Oz називаються Координатними […]...
- Складніші задачі на побудову Розділ 1. Найпростіші геометричні фігури та їх властивості § 19. Складніші задачі на побудову 736. Так. 737. Мал. 401. X належить бісектрисі кута В та колу. Мал. 402. X належить бісектрисі кута В та серединному перпендикуляру ОХ до відрізка ВС. Мал. 403. X належить серединному перпендикуляру ВО до відрізка АС та колу. 738. 1) Спочатку […]...
- Аксіоми стереометрії Геометрія Стереометрія Аксіоми стереометрії I. Яка б не була пряма, існують точки, що належать цій прямій, і точки, що не належать їй. Через будь-які дві точки можна провести пряму, й тільки одну. II. Із трьох точок на прямій одна й тільки одна лежить між двома іншими. III. Кожний відрізок має певну довжину, більшу від нуля. […]...
- Площина. Пряма. Промінь УРОК 11 Тема. Площина. Пряма. Промінь Мета: закріпити знання, здобуті на попередньому уроці, про властивості прямої, площини і променя; розвивати просторову уяву учнів; перевірити засвоєння матеріалу з тем “Відрізок” та “Площина. Пряма. Промінь” під час виконання самостійної роботи. Тип уроку: засвоєння навичок та вмінь. Хід уроку I. Перевірка домашнього завдання та актуалізація опорних знань Усні […]...
- Вправи для повторення розділу 4 Розділ 4. Коло і круг. Геометричні побудови Вправи для повторення розділу 4 До § 21. 756. AB – діаметр, ОС – радіус. AD – хорда. 757. 1) Коло з променем ОК має одну спільну точку. 2) Коло з прямою ОК має дві спільні точки. 758. ?АОВ = ?ВОС за двома сторонами і кутом між ними […]...