Геометричні фігури на площині

Мета: формувати уявлення про геометричні фігури
Дидактичні задачі. Актуалізувати уміння розрізняти прямі, гострі і тупі кути; визначати ці кути у многокутнику; розбивати множини трикутників на підмножини за кутами: ті, що містять один прямий кут, один тупий кут, всі гострі кути; визначати трикутники, в яких всі стороні різної довжини, дві сторони рівні, три сторони рівні; класифікувати трикутники за сторонами; ознайомити з формулами периметра трикутника, в якого всі сторони рівні, лише дві сторони рівні. Формувати
Розвивальна задача: розвивати варіативне мислення учнів при розгляді двох варіантів розв’язання задачі
ХІД УРОКУ
І. МОТИВАЦІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ
Згадайте, коли в житті ви вдавались до вимірювань. Якими вимірювальними приладами користувались? Люди яких професій повсякчас займаються вимірюваннями? Які шкільні знання їм допомагають? Якими із цих знань ви вже володієте? Виявляється, що те, чому ви навчитеся у початковій школі, буде вам у нагоді все життя! Який висновок із цього варто зробити?
ІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ ТА СПОСОБІВ ДІЇ
1. Усне опитування.
Що ви знаєте про пряму, про промінь, відрізок? Чим відрізняється пряма від відрізка; від променю? Чим відрізняється відрізок від променю? Які плоскі фігури вам відомі? Які многокутники ви знаєте? Дати означення прямокутника; квадрата. Чим відрізняється квадрат від прямокутника? Як одержати коло? (Коло одержуємо за допомогою циркуля. Гостру ніжку ставимо на лист паперу і проводимо лінію другою ніжкою циркуля; отримана лінія – коло.) До яких ліній можна віднести коло? (До кривих ліній. Це замкнена крива.)
Що собою представляє крива лінія? (Крива лінія – це множина точок)
Який висновок можна зробити звідси? (Коло – це теж множина точок.)
Назвіть елементи кола. ( Центр кола – місце гострої ніжки циркуля; позначається точкою О. Радіус кола – відрізок, що з’єднує центр кола з будь-якою точкою кола. Можна провести безліч радіусів. Відрізок, який з’єднує дві точки кола і проходить через центр кола – це діаметр. Діаметр кола складається з двох радіусів.)
Чим відрізняється коло від круга? ( Коло – це замкнена крива лінія. Коло лише обмежує круг. Круг – це множина точок площини, обмежена колом разом з цим колом.)
2. Актуалізація уявлення про гострі та тупі кути.
Завдання №1 виконується колективно.
Завдання №1 із робочого зошита виконується з коментарем.
Завдання №2 виконується колективно.




 Трикутники, які містять всі кути гострі: BKL, KMT.
Трикутники, які містять всі кути гострі: BKL, KMT.
Трикутники, які містять прямий кут: CDA, NCP.
Трикутники, які містять тупий кут: ABC.
ІУ. ФОРМУВАННЯ ВМІНЬ І НАВИЧОК. ЗАКРІПЛЕННЯ ВИВЧЕНОГО
1. Закріплення поняття про трикутник. Закріплення поняття про периметр трикутника.
Завдання №3 виконується колективно.
Щоб знайти трикутники, які містять дві рівні сторони, учні мають виміряти лінійкою всі сторони кожного трикутника.

 Трикутники, в яких дві сторони рівні: LKM
Трикутники, в яких дві сторони рівні: LKM
Трикутник, в якого всі сторони рівні: АВС
Пригадуємо означення периметра трикутника, записуємо формулу:
Р = а + в + с. Якщо в трикутнику дві сторони рівні, наприклад а = в, то формула периметра має вигляд: Р = а + а + с =а * 2 + с. Якщо в трикутника всі сторони рівні, то формула периметра виглядатиме так:
Р = а + а + а = а * 3
2. Формування вміння розв’язувати задачі, обернені до задач на знаходження периметра трикутника.
Завдання №4 виконується колективно.
1) Якщо в трикутника всі сторони рівні, то щоб знайти сторону такого трикутника, достатньо периметр розділити порівну на 3. ( Р = а * 3; 39 = 3 * а; а = 39 : 3; а = 13.)
2) Якщо в трикутника дві сторони рівні, то це може бути дві сторони по 24 см. Тоді, щоб знайти довжину третьої сторони, треба від периметра відняти суму ( 24 + 24) або добуток ( 24 * 2). ( Р = а * 2 + с; 54 = 24 * 2 + с; 54 = 48 + с; с = 54 – 48; с = 6.). Дві рівні сторони трикутника не обов’язково можуть бути по 24 см, 24 см – може бути й третя сторона. Тоді, віднявши від периметра число 24 ми одержимо дві інші сторони трикутника, які рівні між собою. ( Р = а * 2 + с; 54 = а * 2 + 24; а * 2 = 54 – 24; а * 2 = 30; а = 30 : 2; а = 15.)
3) Перша сторона 17 мм – це половина другої сторони, тому друга сторона вдвічі більша за 17 мм: 17 мм * 2 = 34 мм. Р = а + в + с; 69 = 17 + 34 + с; 51 + с = 69; с = 69 – 51; с = 18 мм.)
Завдання № 2 із робочого зошита виконується учням самостійно.
Пропонуємо учням серед трьох задач обрати одну із задач і розв’язати її самостійно.
3. Формування уміння розв’язувати складені задачі, що містять величини: швидкість руху, час руху, подоланий шлях.
Записуємо задачу 1 коротко в формі таблиці на дошці.
Розв’язання 1) 25 * 2 = 50 (км) – S1 2) 140 – 50 = 110 (км) – S2 3) 110 : 2 = 55 ( |
Зіставляємо задачу 2 і 1: в задачі 2 дано не суму шляхів, а різницю. Виконуємо на дошці зміни у короткому записі.
З’ясовуємо, як зміна умови вплине на розв’язання? Перша дія не зміниться, якою ми знаходимо шлях першого катера; другою дією так само будемо знаходити шлях другого катера, але вже дією додавання; третя дія так само буде дією ділення, одержане число ділитимемо на 2 і дізнаємось про швидкість другого катера. Учні самостійно записують розв’язання у зошитах.
Завдання №6 виконується учнями самостійно.
4. Вдосконалення уміння знаходити значення виразів на кілька дій. Вдосконалення обчислювальних навичок.
Завдання №8 виконується учнями самостійно.
5. Розвиток логічного мислення учнів.
П’ятдесятиметровий шнур треба розрізати на частини, довжина кожної з яких 2 м. Скільки розрізів треба зробити?
Розв’язання. 50 : 2 – 1 = 24 розрізи.
Відповідь: 24 розрізи.
УІІ. ПОЯСНЕННЯ ЗАВДАННЯ ДЛЯ ДОМАШНЬОЇ РОБОТИ
Завдання №7 – розв’язати задачу способом знаходження однакової величини; після розв’язання змінити одне числове дане і розв’язати задачу способом відношень. Завдання №8 – знайти значення виразів на кілька дій.
УІІ. ПІДСУМОК. РЕФЛЕКСІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ
Поділіться враженнями від змісту уроку – що сподобалось, що виявилось нецікавим. Що, на вашу думку, буде корисним у житті? Які маєте враження від своєї роботи на уроці?
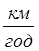 ) – V1
) – V1