Гравітаційна взаємодія. Закон всесвітнього тяжіння
ДИНАМІКА
Урок № 7
Тема. Гравітаційна взаємодія. Закон всесвітнього тяжіння
Мета: сформувати знання про гравітаційну взаємодію тіл; сформулювати та записати закон всесвітнього тяжіння; розкрити фізичний зміст гравітаційної сталої; розвивати допитливість, зацікавити учнів у більш ретельному вивченні теми; сприяти формуванню сучасного світогляду.
Тип уроку: засвоєння нових знань.
ХІД УРОКУ
I. Розминка
Перевертні:
Кон-за, ла-си, жін-тя-ня, ія-є-вза-мод, та-ві-гра-ція.
II. Актуалізація опорних знань учнів Фронтальна
1. Що називають всесвітнім тяжінням?
2. Від чого залежить сила притягання між тілами?
3. Що вам відомо про будову Сонячної системи?
III. Мотивація навчальної діяльності учнів
До моменту відкриття (1667 р.) І. Ньютоном закону всесвітнього тяжіння в астрономії остаточно утвердилась геліоцентрична система світу М. Коперника, згідно з якою всі планети Сонячної системи обертаються навколо Сонця по орбітах, які з наближенням, достатнім для багатьох розрахунків, можна вважати коловими. На початку XVII ст. І. Кеплер встановив кінематичні закони руху планет. Отже, було підготовлено грунт для
IV. Сприйняття та засвоєння нового матеріалу
1. Поняття про гравітаційні сили
На відміну від короткодіючих сильних і слабких взаємодій, електромагнітні і гравітаційні взаємодії мають властивість дальньої дії: їх дія проявляється на дуже великих відстанях. Усі механічні явища в макроскопічному світі визначаються виключно гравітаційними й електромагнітними силами. Дія планет на супутники, політ артилерійських снарядів, плавання тіл в рідині – у всіх цих явищах виявляються гравітаційні сили.
Між фізичними тілами діє сила взаємного притягання. Такі явища, як падіння тіл на Землю, рух Місяця навколо Землі, планет навколо Сонця та інші, відбуваються під дією сил всесвітнього притягання, що називають гравітаційними.
2. Закон всесвітнього тяжіння
Аналізуючи закони Кеплера і закони вільного падіння тіл на Землі, Ньютон дійшов висновку, що сили притягання мають існувати не лише на Землі, а й у космосі. Розглянемо рух деякої планети навколо Сонця, вважаючи її траєкторію колом, а рух рівномірним. На основі першого закону Ньютона можна стверджувати, що на планету має діяти певна сила, яка б не давала можливості планеті полетіти по прямій лінії (згідно із законом інерції) і завертала її щоразу на колову чи близьку до колової орбіти.
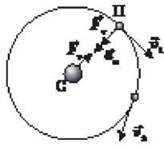
Рис. 1
Інакше кажучи, на планету має діяти сила, напрямлена не вздовж, а поперек руху, яка зумовлює зміну вектора швидкості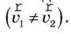 
Другий закон Ньютона дає можливість визначити напрям цієї сили: по радіусу до центра кола, оскільки вектор сили 
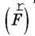збігається за напрямом з вектором прискорення 
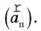У центрі кола міститься Сонце, отже, природно припустити, що ця сила обумовлена взаємодією планети й Сонця.
З третього закону Ньютона випливає, що сила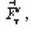 
яка дорівнює за модулем силі 
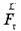і протилежно їй напрямлена, діє на Сонце. Сонце має масу незрівнянно більшу за масу планети, тому зміна руху Сонця дуже незначна.
Прискорення планети під час її руху по коловій орбіті дорівнює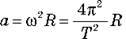 
(звичайне доцентрове прискорення).
Підставивши цей вираз у свій власний закон (a = F/m), Ньютон дістав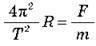 
. Тут F – та сама сила, яка діє на планету з боку Сонця, а m – маса планети. Скориставшись третім законом Кеплера (квадрати періодів обертання двох планет навколо Сонця T1 і T2 відносяться як куби великих півосей їх орбіт R1 i R2:
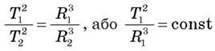(для всіх планет),
Ньютон дійшов висновку, що величина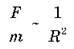 
не залежить від характеристик планети, тобто сила, яка діє на планету з боку Сонця, 
. Міркуючи над тим, від чого могло б залежати значення константи, яку містить цей вираз, Ньютон постулює, що воно визначається лише масою Сонця M. Чому? Просто це йому здавалося природним. Ось так і виник знаменитий і одночасно такий звичний сьогодні вираз:
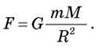
Закон, який характеризує сили притягання, уперше сформулював Ньютон 1687 року під час вивчення руху Місяця навколо Землі. Це закон всесвітнього тяжіння: будь-які дві матеріальні точки притягуються одна до одної із силою, прямо пропорційною добутку їх мас і обернено пропорційною квадрату відстані між ними:
Де m1 і m2 – маси матеріальних точок; R – відстань між ними; G – гравітаційна стала.
3. Гравітаційна стала
Коефіцієнт пропорційності G – гравітаційна стала, що чисельно дорівнює силі, з якою притягуються два тіла масою по 1 кг кожне, перебуваючи на відстані 1 м одне від одного. Гравітаційну сталу визначено експериментальним шляхом. Вперше це зробив англійський вчений Кавендіш за допомогою крутильного динамометра (крутильних терезів).
У СІ гравітаційна стала має значення 
. Отже, два тіла масою 1 кг кожне, що знаходяться одне від одного на відстані 1 м, взаємно притягуються гравітаційною силою, що дорівнює 6,67-10-11 H.
Закон всесвітнього тяжіння справедливий лише для матеріальних точок. Строго доведено, що силу притягання між двома тілами можна визначити за формулою (1) у таких випадках:
1) якщо обидва тіла є однорідними кулями, тоді m1 і m2 – їх маси, R – відстань між центрами куль;
2) одне із тіл є матеріальною точкою, а друге – однорідна куля, тоді m1 і m2 – маса кулі і точки, R – відстань між їхніми центрами мас.
Дві сили взаємодії, які діють на кожне із взаємодіючих тіл, однакові за величиною і протилежні за напрямом у цілковитій відповідності з третім законом Ньютона. Вони напрямлені вздовж прямої, яка з’єднує матеріальні точки; їх називають центральними силами. Гравітаційна взаємодія між тілами, що описується законом всесвітнього тяжіння, здійснюється за посередництвом гравітаційного поля (поля тяжіння). У кожній точці поля тяжіння на вміщене туди тіло діє сила тяжіння, пропорційна масі цього тіла. Сила тяжіння не залежить від середовища, у якому знаходяться тіла.
Поле тяжіння має специфічну властивість, яка полягає в тому, що під час перенесення тіла масою m з однієї точки поля тяжіння в іншу робота сили тяжіння не залежить від траєкторії руху тіла, а залежить тільки від положення в цьому полі початкової і кінцевої точок переміщення тіла. Сили, що мають подібну властивість, називають консервативними, а поле таких сил – потенціальним.
Закон всесвітнього тяжіння дозволив Ньютону пояснити рух планет, морські припливи та відпливи. Пізніше астрономи за допомогою цього закону відкрили “на кінчику пера” найбільш віддалені планети нашої Сонячної системи – Нептун і Плутон. На підставі цього закону на багато років у перед передбачають сонячні та місячні затемнення, розраховують рух космічних кораблів.
V. Осмислення об’єктивних зв’язків. Узагальнення задач
Розв’язування задач
1. Як зміниться сила гравітаційної взаємодії двох тіл однієї маси, якщо:
А) маса одного тіла збільшиться у 2 рази, 3 рази, 7 разів;
Б) маса двох тіл зменшиться у 2, 3, 7 разів;
В) відстань між тілами збільшиться у 2, 3, 7 разів?
2. Визначити мінімальний період обертання супутника нейтронної зорі, густина речовини якої 1017 кг/м3.
Дано: ? = 1017 кг/м3
Знайти: T – ?
Розв’язання
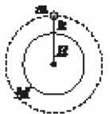
Рис. 2
Згідно із законом всесвітнього тяжіння між супутником масою m і планетою масою M (якщо вважати висоту h супутника над планетою значно меншою від радіуса планети h << R) діє сила
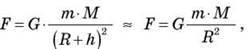
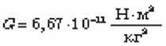– гравітаційна стала.
Супутник рухається по коловій орбіті, отже, на супутник діє доцентрова сила:
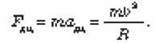
Отже,
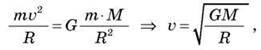
Де 
– швидкість руху супутника.
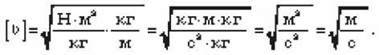
Мінімальний період обертання:
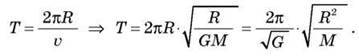
Середня густина планети: ? = М/V, де M – маса планети, V – її об’єм.
Об’єм кулі:
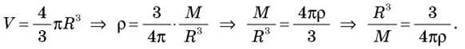
Підставимо отриманий вираз у формулу для періоду:
Відповідь: 1,19-10-3 c.
3. З якою силою взаємодіють Місяць і Земля, якщо маса Місяця 7-1022 кг, а Землі 6-1024 кг. Відстань між ними 384 000 км.
VI. Підсумки уроку
Обговорення питань
1. Що спільного між падінням тіл на Землю, обертанням Місяця навколо Землі, припливами і відпливами?
2. Чому до Ньютона ніхто не зміг пояснити природу руху планет?
3. Як рухалися б небесні тіла, якби вони не притягувалися одне до одного?
4. Як залежить сила притягання двох тіл від їхніх мас і від відстані між ними?
VII. Домашнє завдання
Розв’язати задачі:
1. Якою є відстань між кулями масою 100 кг кожна, які перебувають у спокої, якщо вони притягуються одна до одної із силою, що дорівнює 0,1 Н?
2. Визначте масу і середню густину Землі. Радіус Землі вважати рівним 6400 км.
3. Придумати та записати в зошит зміст задачі на використання закону всесвітнього тяжіння (брати реальні числа).
(1 votes, average: 5.00 out of 5)
Loading...