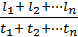КОЛИВАЛЬНИЙ РУХ. АМПЛІТУДА. ПЕРІОД І ЧАСТОТА КОЛИВАНЬ
Розділ 2 МЕХАНІЧНИЙ РУХ
& 13. КОЛИВАЛЬНИЙ РУХ. АМПЛІТУДА. ПЕРІОД І ЧАСТОТА КОЛИВАНЬ
Ще в давнину люди, спостерігаючи за Сонцем і Місяцем, визначили одиниці часу: рік, місяць, добу та ін. Був створений сонячний годинник, потім з’явилися водяний, вогневий і пісковий годинники. Проте справжня революція в конструкції годинників відбулася після з’ясування властивостей коливального руху. А от яких саме властивостей – дізнаєтесь із цього параграфа.
1. Знайомимося з коливальним рухом
Підвісимо тягарець на нитку, відхилимо його
2. Вивчаємо маятники
Тягарець, що коливається на нитці або на пружині, – це приклад найпростішого маятника.
Маятник – це тверде тіло, яке здійснює коливання внаслідок притягання до Землі або внаслідок дії пружини.
Маятники використовують у багатьох фізичних приладах. Особливо важливим є використання маятників
Маятники, в яких тіло коливається завдяки дії пружини, називають пружинними маятниками (рис. 13.2). Коливання пружинного маятника залежать від властивостей пружини і маси тіла.
Маятники, які коливаються завдяки притяганню до Землі, називають фізичними маятниками (рис. 13.3). Їх коливання є доволі складними, адже залежать від маси, геометричних розмірів, форми маятника тощо.
Щоб розміри і форма тіла не впливали на його коливання, слід узяти нитку, довжина якої є досить великою порівняно з розмірами тіла, – у такому випадку тіло можна вважати матеріальною точкою. При цьому нитка має бути легкою і досить тонкою, а щоб під час коливань тіло було на незмінній відстані від точки підвісу, – нерозтяжною.
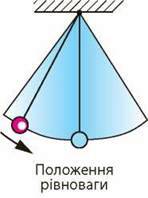
Рис. 13.1. Коливальний рух – це періодичний рух
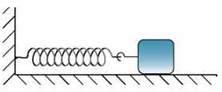
Рис. 13.2. Приклад найпростішого пружинного маятника

Рис. 13.3. Приклади фізичних маятників
Невелика металева кулька діаметром 1-2 см, підвішена на тонкій нерозтяжній нитці завдовжки 1-2 м, цілком може слугувати за маятник, на коливання якого не впливатимуть розміри, маса тіла та властивості нитки (рис. 13.4)*.
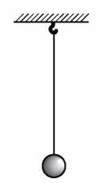
Рис. 13.4. Металева кулька на довгій нерозтяжній нитці є досить зручною для вивчення основних властивостей коливань
3. Дізнаємося про амплітуду коливань
Спостерігаючи за коливаннями маятника, неважко побачити, що є певна максимальна відстань, на яку тіло, що коливається, віддаляється від положення рівноваги. Цю відстань називають амплітудою коливань (рис. 13.5).
Амплітуда коливань – це фізична величина, що дорівнює максимальній відстані, на яку відхиляється тіло від положення рівноваги під час коливань.
Амплітуду коливань позначають символом A. Одиниця амплітуди коливань в СІ – метр: [A ] = м.
За одне коливання тіло проходить шлях l0, який приблизно дорівнює чотирьом амплітудам: l0 = 4A *.
4. Визначаємо період і частоту коливань
Коливальний рух є періодичним рухом, тому він характеризується такими фізичними величинами, як період коливань і частота коливань.
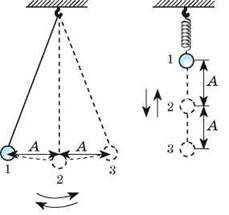
Рис. 13.5. Рух кульки від положення 1 до положення 3 (через положення 2), а потім знову до положення 1 – це одне коливання; А – амплітуда коливань
* У цьому випадку довжина нитки вважається також довжиною маятника.
* У випадку з нитяним маятником ця рівність є приблизною, оскільки тіло рухається по дузі кола, довжина якої більша за відстань, яку називають амплітудою коливань. Але якщо амплітуда коливань є малою (набагато меншою від довжини маятника), цією різницею зазвичай нехтують.
Період коливань – це фізична величина, що дорівнює часу, за який відбувається одне коливання.
Період коливань, як і період рівномірного руху по колу, позначають символом T і обчислюють за формулою:
T = 
Де t – час спостереження; N – кількість коливань за цей час. Одиниця періоду коливань в СІ – секунда: [T] = с.
Частота коливань – це фізична величина, яка дорівнює кількості коливань за одиницю часу.
Частоту коливань позначають символом v (“ню”) і обчислюють за формулою:
V = 
Одиниця частоти коливань в СІ – герц (Гц) (названа на честь Генріха Герца (рис. 13.6)).
Якщо тіло за одну секунду робить одне коливання, то частота його коливань дорівнює одному герцу: 1 Гц =  .
.
Частота v і період T коливань є взаємно оберненими величинами:
V = 

Рис. 13.6. Генріх Рудольф Герц (1857-1894) – німецький фізик, один із засновників теорії електричних коливань
Маятники мають дуже важливу властивість: якщо амплітуда коливань маятника набагато менша від його довжини, то частота і період коливань маятника не залежать від амплітуди.
Цю властивість малих коливань відкрив Галілео Галілей*, і саме вона покладена в основу роботи механічних годинників.
5. Розрізняємо затухаючі і незатухаючі коливання
Виведемо гойдалку зі стану рівноваги та відпустимо. Гойдалка почне коливатися. Такі коливання називають вільними.
Якщо на гойдалку не впливати, то через деякий час амплітуда її коливань помітно зменшиться, а згодом коливання припиняться зовсім.
Коливання, амплітуда яких із часом зменшується, називають затухаючими коливаннями.
* Галілео Галілей зробив це відкриття, спостерігаючи в храмі коливання лампади, підвішеної на ланцюзі, і порівнюючи частоту цих коливань із частотою биття власного пульсу.
Вільні коливання завжди є затухаючими. Затухають із плином часу вільні коливання било дзвона, струни гітари, гілки дерева…
Що слід зробити, щоб амплітуда коливань гойдалки з часом не зменшувалась, тобто щоб її коливання були незатухаючими?
Незатухаючі коливання – це коливання, амплітуда яких не змінюється з часом.
Незатухаючі коливання здійснює, наприклад, голка швацької машинки, доки працює її механізм (рис. 13.7).

Рис. 13.7. Коливання голки швацької машинки – приклад незатухаючих коливань
6. Учимося розв’язувати задачі
Задача. Невелику важку кульку, підвішену на нерозтяжній нитці завдовжки 1 м, відхилили від положення рівноваги та відпустили. За 30 с кулька здійснила 15 коливань. Яку відстань пройде кулька за 36 с, якщо амплітуда коливань – 5 см? Коливання вважайте незатухаючими.
Аналіз фізичної проблеми. Амплітуда коливань набагато менша від довжини нитки, тому можна вважати, що за одне коливання кулька проходить шлях, який дорівнює чотирьом амплітудам (4A).
Якщо визначити кількість коливань за 36 с, то можна знайти відстань, яку подолала кулька. Кількість коливань знайдемо, визначивши час одного коливання, тобто період коливань.
Задачу розв’язуватимемо в поданих одиницях.
Дано:
T1= 30 c
N1= 15
T2 = 36 c
A = 5 см
Знайти:
L – ?
Пошук математичної моделі, розв’язання.
Знайдемо період коливань: T = 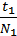 =
= 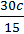 = 2 с.
= 2 с.
Знайдемо кількість коливань за 36 с: N2 = 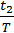 =
= 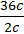 = 18.
= 18.
Визначимо шлях, який долає кулька за одне коливання: l0 = 4A = 4 ∙ 5 см = 20 см.
Визначимо шлях, який подолає кулька за 36 с:
L = N2 ∙ l0 = 18 ∙ 20 см = 360 см = 3,6 м.
Аналіз результатів. За одне коливання кулька проходить 20 см; час коливань більший за період коливань, тому пройдена кулькою відстань буде більшою за 20 см. Отже, результат є правдоподібним. Відповідь: l = 3,6 м.
Підбиваємо підсумки
Коливальний рух (коливання) є періодичним рухом. Розрізняють затухаючі і незатухаючі коливання.
Амплітуда А коливань – це фізична величина, що дорівнює максимальній відстані, на яку тіло відхиляється від положення рівноваги.
Період Т коливань – це фізична величина, що дорівнює часу, за який відбувається одне коливання: T =  . Одиниця періоду коливань в СІ – секунда (с).
. Одиниця періоду коливань в СІ – секунда (с).
Частота v коливань – це фізична величина, яка дорівнює кількості коливань за одиницю часу: v =  . Одиниця частоти коливань в СІ – герц (Гц).
. Одиниця частоти коливань в СІ – герц (Гц).
Частота і період коливань є взаємно оберненими величинами: v =  .
.
Контрольні запитання
1. Чому коливальний рух є періодичним? 2. Наведіть приклади коливань. 3. Наведіть приклади маятників. 4. Дайте означення амплітуди, періоду, частоти коливань. У яких одиницях вимірюють ці фізичні величини? 5. Яка залежність пов’язує між собою частоту і період коливань? 6. Які коливання називають затухаючими? незатухаючими?
Вправа № 13
1. Під час коливань тіло рухається від крайнього лівого положення до крайнього правого. Відстань між цими двома положеннями становить 4 см. Визначте амплітуду коливань тіла.
2. За хвилину маятник здійснив 30 коливань. Визначте період коливань маятника.
3. Період коливань дорівнює 0,5 с. Визначте частоту коливань.
4. Скільки коливань здійснить тіло за 2 хв, якщо частота його коливань становить 4 Гц?
5. Наведіть не згадані в параграфі приклади коливальних рухів. З’ясуйте, які це коливання: затухаючі або незатухаючі.
6. Поплавок, що коливається на воді, піднімається та пірнає 6 разів за 3 секунди. Який шлях подолає поплавок за хвилину, якщо відстань між його крайніми положеннями становить 5 см?
7. “Котра година?” – це питання ставлять протягом багатьох століть. Щоб відповісти на нього, існувало й зараз існує багато пристроїв. Один з них – маятниковий годинник. Дізнайтесь про історію його створення і підготуйте повідомлення.
Експериментальне завдання
“Резонанс”. Прив’яжіть до невеликого важкого тіла нитку завдовжки 45-50 см. Однією рукою візьміть нитку за вільний кінець, а другою відхиліть тіло від положення рівноваги. Маятник почне коливатися. Визначте частоту його вільних коливань.
Зупиніть маятник. Потім почніть дуже повільно рухати рукою з маятником з одного боку в інший (див. Малюнок). Слідкуйте, щоб амплітуда коливань руки не змінювалась; руку достатньо переміщувати на 1-2 см. Поступово збільшуйте частоту коливань руки і спостерігайте за маятником. “Спіймайте” такий момент, коли маятник розгойдається дуже сильно, тобто виникне резонанс. Визначте частоту коливань руки в той момент, коли амплітуда коливань маятника є найбільшою. Дізнайтеся, за якої умови настає резонанс, порівнявши знайдені значення частоти вільних коливань маятника і частоти коливань руки.

ЛАБОРАТОРНА РОБОТА № 5
Тема. Дослідження коливань нитяного маятника.
Мета: визначити амплітуду і період коливань нитяного маятника; переконатися на досліді, що період коливань маятника не залежить від амплітуди його коливань і маси тягарця, проте залежить від довжини нитки.
Обладнання: дві невеличкі важкі кульки відомих мас; дві міцні нерозтяжні нитки завдовжки 1,05-1,1 м; лінійка (мірна стрічка); штатив із муфтою та кільцем; секундомір.
ВКАЗІВКИ ДО РОБОТИ
Підготовка до експерименту
1. Перед тим як виконувати роботу, переконайтеся, що ви знаєте відповіді на такі запитання:
1) Що називають амплітудою коливань?
2) За якою формулою можна обчислити період коливань?
2. Визначте ціну поділки шкали лінійки.
3. Запишіть значення мас кульок до табл. 2.
4. Закріпіть кульки на нитках.
Експеримент. Опрацювання результатів експерименту
Суворо дотримуйтесь інструкції з безпеки (див. форзац підручника).
1. Установіть на краю стола штатив. Біля його верхнього кінця закріпіть за допомогою муфти кільце й підвісьте до нього одну з кульок на нитці так, щоб довжина одержаного маятника становила 1 м. Пересуваючи муфту вздовж штатива, установіть її на такій висоті, щоб кулька була на відстані 3-5 см від розташованої на підлозі лінійки (див. Малюнок).
2. Дослідіть залежність періоду коливань маятника від його амплітуди. Для цього:
1) відхиливши маятник на відстань 2-3 см від положення рівноваги і відпустивши, виміряйте час, за який маятник виконає 20 коливань; визначте період коливань;
2) повторіть дослід, збільшивши амплітуду коливань до 5-6 см;
3) результати вимірювань та обчислень занесіть до табл. 1.
Таблиця 1
Номер досліду | Довжина нитки l, м | Амплітуда коливань A, м | Число коливань N | Час коливань t, с | Період коливань T, с |
1 | 1 | ||||
2 | 1 |
3. Дослідіть залежність періоду коливань маятника від його маси. Для цього:
1) перенесіть із табл. 1 до табл. 2 результати досліду № 1;
2) повторіть дослід для другого маятника (іншої маси); амплітуда коливань має становити 2-3 см. Зверніть увагу: довжини першого та другого маятників мають бути однаковими.
3) результати вимірювань і обчислень занесіть до табл. 2.
Таблиця 2
Номер досліду | Довжина нитки l, м | Маса кульки m, кг | Число коливань N | Час коливань t, с | Період коливань T, с |
1 | 1 | ||||
3 | 1 |
4. Дослідіть залежність періоду коливань маятника від його довжини. Для цього:
1) перенесіть із табл. 1 до табл. 3 результати досліду № 1;
2) повторіть дослід, зменшивши довжину першого маятника до 25 см; амплітуда коливань має становити 2-3 см;
3) результати вимірювань і обчислень занесіть до табл. 3.
Таблиця 3
Номер досліду | Довжина нитки l, м | Число коливань N | Час коливань t, с | Період коливань T, с |
1 | 1 | |||
4 | 0,25 |
Аналіз експерименту та його результатів
Проаналізувавши результати, зробіть висновок, у якому зазначте: 1) які величини ви навчилися вимірювати; 2) які чинники вплинули на точність одержаних результатів; 3) чи залежить період коливань маятника від амплітуди коливань, маси тягарця, довжини маятника.
Творче завдання
Не виконуючи вимірювань, визначте період коливань маятника завдовжки 4 м, амплітуда коливань якого 10 см, а маса – 300 г. Вважайте, що маятник розташований у тому самому кабінеті, де ви виконували лабораторну роботу. Свою відповідь обгрунтуйте.
ПІДБИВАЄМО ПІДСУМКИ РОЗДІЛУ 2 “Механічний рух”
У розділі 2 ви вивчали механічний рух та його характеристики, дізналися про види механічного руху – прямолінійний рух, рух по колу, коливальний рух.
1. Ви ознайомились із деякими основними поняттями механіки.
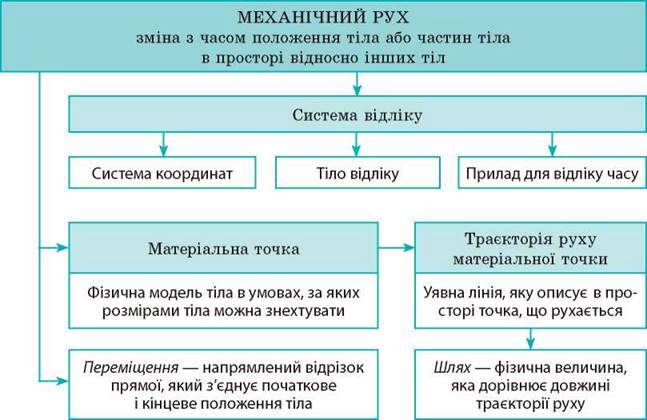
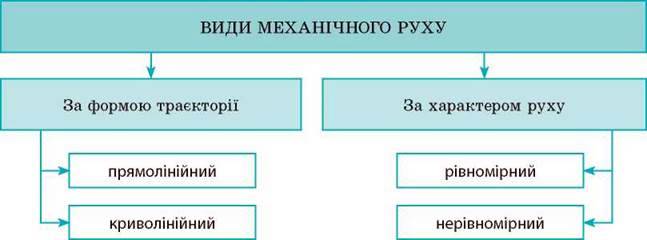
2. Ви навчилися розрізняти види механічного руху.
3. Ви навчилися досліджувати рівномірний рух за допомогою графіків шляху та графіків швидкості руху.
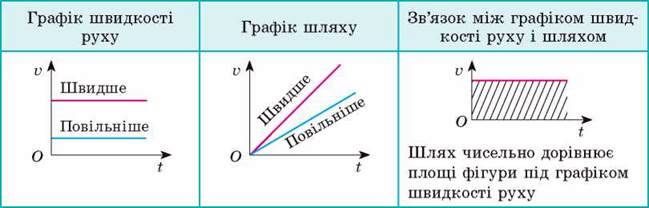
4. Ви дослідили деякі механічні рухи.
Форма траєкторії | Фізичні величини, які характеризують механічний рух | ||
Шлях l [ l ] = м | Час руху t [ t ] = c | Швидкість руху v [ v ] = м/с | |
Рівномірний рух | |||
Будь-яка лінія | L = vt | T = | V = |
Рівномірний прямолінійний рух | |||
Пряма лінія | L = s = vt | T = | V = |
Нерівномірний рух | |||
Будь-яка лінія | L = l1 + l2 + … + ln | T = t1 + t2 + … + tn | V = |
Форма траєкторії | Фізичні величини, які характеризують механічний рух | ||
Період T [ T ] = с | Частота n або v [ n ] = об/с; [v] = Гц | Шлях за період l [ l ] = м | |
Рівномірний рух по колу | |||
Коло | T = | N = | L = 2 пR, Де R – радіус кола |
Коливальний рух | |||
Відрізок прямої, дуга кола | T = | V = | L0 = 4 A, Де А – амплітуда коливань |
Завдання для самоперевірки до розділу 2 “Механічний рух”
У завданнях 1-9 виберіть одну правильну відповідь.
1. (1 бал) Потяг, який прямує від однієї станції до іншої, перебуває у стані спокою відносно:
А) центра Землі;
Б) пасажира, що сидить у кріслі вагона;
В) точок на ободі колеса вагона;
Г) рейок, по яких він рухається.
2. (1 бал) Швидкість рівномірного руху – це фізична величина, яка дорівнює:
А) добутку шляху, який подолало тіло, і часу руху;
Б) відношенню часу руху до шляху, який подолало тіло;
В) половині суми початкової та кінцевої швидкостей руху;
Г) відношенню шляху, який подолало тіло, до часу руху.
3. (1 бал) Обертова частота – це фізична величина, яка чисельно дорівнює:
А) часу одного оберту;
Б) кількості обертів за одиницю часу;
В) кількості обертів за весь час руху;
Г) часу, за який тіло здійснює 10 обертів.
4. (1 бал) Період малих коливань нитяного маятника:
А) залежить від довжини нитки;
Б) залежить від маси тягарця;
В) залежить від амплітуди коливань;
Г) не залежить від земного тяжіння.
5. (2 бали) Космічний корабель протягом 20 с рухався зі швидкістю 10 000 м/с. Яку відстань подолав корабель за цей час?
А) 5 км; б) 20 км; в) 200 км; г) 500 км.
6. (2 бали) Потяг рухався із середньою швидкістю 40 м/с. Скільки часу тривала подорож між двома містами, якщо відстань між ними 624 км? а) 1 год 34 хв; б) 4,2 год; в) 4 год20 хв; г) 15,6 год.
7. (2 бали) Гвинт гелікоптера за 0,5 хвилини здійснює 600 обертів. Чому дорівнює період обертання гвинта?
А) 0,8 мс; б) 50 мс; в) 5 с; г) 2 хв.
8. (2 бали) Частота коливань нитяного маятника дорівнює 2 Гц. Скільки коливань здійснює цей маятник за 1 хв?
А) 0,5; б) 2; в) 30; г) 120.
9. (3 бали) Півгодини хлопчик їхав на велосипеді зі швидкістю 24 км/год, а потім ішов пішки 6 км зі швидкістю 4 км/год. Визначте середню швидкість руху хлопчика.
А) 9 км/год; б) 14 км/год; в) 20 км/год; г) 28 км/год.
10. (3 бали) За графіком залежності шляху від часу для рівномірного руху (рис. 1) визначте швидкість руху тіла. Відповідь подайте в м/с і км/год.
11. (3 бали) У кают-компанії судна, яке здійснює морську подорож у 250 км, розташований годинник. Скільки коливань здійснить маятник годинника за час подорожі, якщо період його коливань дорівнює 0,5 с, а середня швидкість руху судна – 10 м/с?
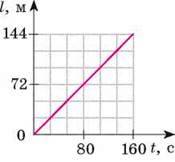
Рис. 1
12. (3 бали) Турист ішов гірською стежкою, рухаючись зі швидкістю 2 км/год, а потім повернувся до місця свого старту, рухаючись зі швидкістю 6 км/год. Якою була середня швидкість руху туриста на всьому шляху?
13. (4 бали) Використовуючи дані рис. 2, визначте, через який час зустрінуться автомобілі.
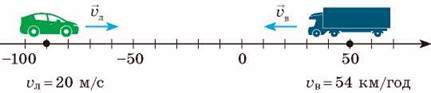
Рис. 2
14. (4 бали) На рис. 3 наведено графік швидкості руху автомобіля. Визначте максимальну швидкість руху автомобіля та весь шлях, що він подолав.
15. (5 балів) Автомобіль подолав 400 км. Відомо, що першу половину всього часу руху він рухався зі швидкістю 90 км/год, а за другу половину часу руху проїхав 175 км. Якою була швидкість руху автомобіля на другій ділянці шляху? Визначте середню швидкість руху автомобіля на всьому шляху. Рух автомобіля на обох ділянках вважайте рівномірним.
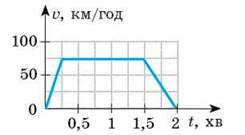
Рис. 3
Звірте ваші відповіді з наведеними наприкінці підручника. Позначте завдання, які ви виконали правильно, і полічіть суму балів. Потім цю суму поділіть на три. Одержане число відповідатиме рівню ваших навчальних досягнень.
Тренувальні тестові завдання з комп’ютерною перевіркою ви знайдете на електронному освітньому ресурсі “Інтерактивне навчання”.
Космодром на екваторі
Практично всі технічні новинки, що з’явилися за останні сто років, створено за такою схемою: етап 1 – учені відкривають новий ефект (явище); етап 2 – інженери-фахівці створюють пристрій (прилад), дія якого базується на використанні відкритого ефекту (явища).
Таким чином, інженери-механіки працюють над створенням нових, удосконалених автомобілів і верстатів, інженери-оптики – фотоапаратів і телескопів, інженери-електрики – акумуляторів і електромоторів тощо.
Прочитавши енциклопедичні сторінки в цьому підручнику, ви переконаєтеся в тому, що інженерові потрібні знання не тільки зі своєї спеціальності – він має широко застосовувати відомості з інших наукових галузей.
Як найдалі кинути камінь, або Чому космодроми будують поблизу екватора
Більшість жителів Землі гадки не мають, як улаштовані ракети й космічні станції, але майже всім відомо, що космос – це дуже багато витрат. Знають про це й інженери – конструктори ракет. І щоб зменшити, наприклад, витрати на доправлення вантажів на орбіту, вони намагаються знаходити в тому числі всілякі нетрадиційні рішення. Наведемо приклад.
Згадайте ваші ігри на дитячій каруселі: ви розганяєте карусель і застрибуєте на неї. При цьому найскладніше втримуватися на краю каруселі, що швидко обертається, – “невідома сила” намагається скинути вас. Саме цей фізичний ефект використовують спортсмени – метальники молота, розкручуючи металеве ядро на тросі (цікаво, що світовий рекорд у метанні молота приблизно в чотири рази більший, ніж у штовханні ядра, – близько 86 м і 22 м відповідно, при цьому маси обох снарядів є однаковими); на тому самому ефекті грунтується дія пращі – давньої метальної зброї.


Космічні кораблі виводитиме на орбіту ракета-носій “Циклон-4”
Конструктори ракет напевне добре знали фізику, адже вирішили “полегшити” старт космічного корабля, використовуючи як карусель Землю. І ось як. Відомо, що Земля обертається навколо своєї осі, при цьому зрозуміло, що найшвидше обертаються території навколо екватора. Запускаючи ракету з екватора, за інших однакових умов на орбіту можна “закинути” приблизно на 20% більше корисного вантажу. Тому, наприклад, космодром Європейського космічного агентства – космодром Куру – розміщений у Французькій Гвіані, безпосередньо поблизу екватора.
А що ж робити тим країнам, які розташовані в середніх широтах, наприклад Україні?
Майже 20 років тому почався грандіозний міжнародний проект за участю України, що отримав назву “Сі-Лонч” (у перекладі з англійської – “Морський старт”). Інженери вирішили: якщо країни не мають суходільної території на екваторі, слід здійснювати запуски ракет із морської поверхні. Як же цю ідею було реалізовано?
Зрозуміло, що для розміщення космодрому потрібна значна територія, практично цілий штучний острів. На щастя, подібні “острови” вже були створені, щоправда з іншою метою, – це плавучі платформи для видобутку нафти зі дна морів. Як ракета-носій у проекті “Сі-Лонч” була використана українська ракета “Зеніт” – одна з найкращих у світі. У рамках проекту було здійснено 36 пусків.
Українські фахівці одночасно з участю в “Морському старті” працювали в спільному українсько-бразильському проекті зі створення пускового майданчика на космодромі Алкантара (на півдні Бразилії, 300 км до екватора).
І знову “родзинкою” проекту з українського боку була ракета-носій. Цього разу – “Циклон-4”.
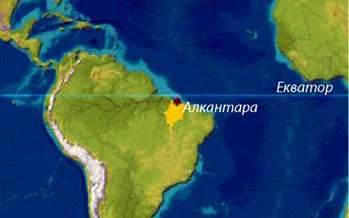
Місце розташування бразильського космодрому Алкантара

Ракети-носії українського виробництва
Теми рефератів і повідомлень
1. Еволюція приладів для вимірювання часу.
2. Способи відліку часу. Календарі.
3. Надшвидкі потяги світу.
4. Рекорди швидкості серед живих істот і серед технічних пристроїв. Порівняння.
5. Історія рекордів швидкості на суднах.
6. Історія рекордів швидкості на автомобілях.
7. Яким буде транспорт майбутнього.
8. Україна – космічна держава.
9. Марсіанська наукова лабораторія: марсохід “К’юріосіті”.
10. Комета Чурюмова – Герасименко.
11. Обертальний рух у природі й техніці.
12. Роль маятника у вивченні фізичних властивостей Землі.
Теми експериментальних досліджень
1. Вимірювання часу реакції людини.
2. Визначення середньої швидкості руху людини під час прогулянки.
3. Визначення середньої швидкості польоту м’яча.
4. Побудова графіків механічного руху паперового літачка та визначення середньої швидкості його руху.
5. Коливальні процеси в живій природі.
6. Коливальні процеси в техніці.
7. Коливальні процеси в неживій природі.
& 13. КОЛИВАЛЬНИЙ РУХ. АМПЛІТУДА. ПЕРІОД І ЧАСТОТА КОЛИВАНЬ
Ще в давнину люди, спостерігаючи за Сонцем і Місяцем, визначили одиниці часу: рік, місяць, добу та ін. Був створений сонячний годинник, потім з’явилися водяний, вогневий і пісковий годинники. Проте справжня революція в конструкції годинників відбулася після з’ясування властивостей коливального руху. А от яких саме властивостей – дізнаєтесь із цього параграфа.
1. Знайомимося з коливальним рухом
Підвісимо тягарець на нитку, відхилимо його від положення рівноваги і відпустимо. Тягарець почне коливатися, тобто рухатися від одного крайнього положення до іншого, повторюючи свій рух через певний інтервал часу. Таким чином, коливальний рух має важливу спільну рису з рівномірним рухом по колу: обидва рухи є періодичними (рис. 13.1).
2. Вивчаємо маятники
Тягарець, що коливається на нитці або на пружині, – це приклад найпростішого маятника.
Маятник – це тверде тіло, яке здійснює коливання внаслідок притягання до Землі або внаслідок дії пружини.
Маятники використовують у багатьох фізичних приладах. Особливо важливим є використання маятників у годинниках: періодичність коливань дає можливість здійснювати відлік часу.
Маятники, в яких тіло коливається завдяки дії пружини, називають пружинними маятниками (рис. 13.2). Коливання пружинного маятника залежать від властивостей пружини і маси тіла.
Маятники, які коливаються завдяки притяганню до Землі, називають фізичними маятниками (рис. 13.3). Їх коливання є доволі складними, адже залежать від маси, геометричних розмірів, форми маятника тощо.
Щоб розміри і форма тіла не впливали на його коливання, слід узяти нитку, довжина якої є досить великою порівняно з розмірами тіла, – у такому випадку тіло можна вважати матеріальною точкою. При цьому нитка має бути легкою і досить тонкою, а щоб під час коливань тіло було на незмінній відстані від точки підвісу, – нерозтяжною.

Рис. 13.1. Коливальний рух – це періодичний рух

Рис. 13.2. Приклад найпростішого пружинного маятника

Рис. 13.3. Приклади фізичних маятників
Невелика металева кулька діаметром 1-2 см, підвішена на тонкій нерозтяжній нитці завдовжки 1-2 м, цілком може слугувати за маятник, на коливання якого не впливатимуть розміри, маса тіла та властивості нитки (рис. 13.4)*.

Рис. 13.4. Металева кулька на довгій нерозтяжній нитці є досить зручною для вивчення основних властивостей коливань
3. Дізнаємося про амплітуду коливань
Спостерігаючи за коливаннями маятника, неважко побачити, що є певна максимальна відстань, на яку тіло, що коливається, віддаляється від положення рівноваги. Цю відстань називають амплітудою коливань (рис. 13.5).
Амплітуда коливань – це фізична величина, що дорівнює максимальній відстані, на яку відхиляється тіло від положення рівноваги під час коливань.
Амплітуду коливань позначають символом A. Одиниця амплітуди коливань в СІ – метр: [A ] = м.
За одне коливання тіло проходить шлях l0, який приблизно дорівнює чотирьом амплітудам: l0 = 4A *.
4. Визначаємо період і частоту коливань
Коливальний рух є періодичним рухом, тому він характеризується такими фізичними величинами, як період коливань і частота коливань.

Рис. 13.5. Рух кульки від положення 1 до положення 3 (через положення 2), а потім знову до положення 1 – це одне коливання; А – амплітуда коливань
* У цьому випадку довжина нитки вважається також довжиною маятника.
* У випадку з нитяним маятником ця рівність є приблизною, оскільки тіло рухається по дузі кола, довжина якої більша за відстань, яку називають амплітудою коливань. Але якщо амплітуда коливань є малою (набагато меншою від довжини маятника), цією різницею зазвичай нехтують.
Період коливань – це фізична величина, що дорівнює часу, за який відбувається одне коливання.
Період коливань, як і період рівномірного руху по колу, позначають символом T і обчислюють за формулою:
T = 
Де t – час спостереження; N – кількість коливань за цей час. Одиниця періоду коливань в СІ – секунда: [T] = с.
Частота коливань – це фізична величина, яка дорівнює кількості коливань за одиницю часу.
Частоту коливань позначають символом v (“ню”) і обчислюють за формулою:
V = 
Одиниця частоти коливань в СІ – герц (Гц) (названа на честь Генріха Герца (рис. 13.6)).
Якщо тіло за одну секунду робить одне коливання, то частота його коливань дорівнює одному герцу: 1 Гц =  .
.
Частота v і період T коливань є взаємно оберненими величинами:
V = 

Рис. 13.6. Генріх Рудольф Герц (1857-1894) – німецький фізик, один із засновників теорії електричних коливань
Маятники мають дуже важливу властивість: якщо амплітуда коливань маятника набагато менша від його довжини, то частота і період коливань маятника не залежать від амплітуди.
Цю властивість малих коливань відкрив Галілео Галілей*, і саме вона покладена в основу роботи механічних годинників.
5. Розрізняємо затухаючі і незатухаючі коливання
Виведемо гойдалку зі стану рівноваги та відпустимо. Гойдалка почне коливатися. Такі коливання називають вільними.
Якщо на гойдалку не впливати, то через деякий час амплітуда її коливань помітно зменшиться, а згодом коливання припиняться зовсім.
Коливання, амплітуда яких із часом зменшується, називають затухаючими коливаннями.
* Галілео Галілей зробив це відкриття, спостерігаючи в храмі коливання лампади, підвішеної на ланцюзі, і порівнюючи частоту цих коливань із частотою биття власного пульсу.
Вільні коливання завжди є затухаючими. Затухають із плином часу вільні коливання било дзвона, струни гітари, гілки дерева…
Що слід зробити, щоб амплітуда коливань гойдалки з часом не зменшувалась, тобто щоб її коливання були незатухаючими?
Незатухаючі коливання – це коливання, амплітуда яких не змінюється з часом.
Незатухаючі коливання здійснює, наприклад, голка швацької машинки, доки працює її механізм (рис. 13.7).

Рис. 13.7. Коливання голки швацької машинки – приклад незатухаючих коливань
6. Учимося розв’язувати задачі
Задача. Невелику важку кульку, підвішену на нерозтяжній нитці завдовжки 1 м, відхилили від положення рівноваги та відпустили. За 30 с кулька здійснила 15 коливань. Яку відстань пройде кулька за 36 с, якщо амплітуда коливань – 5 см? Коливання вважайте незатухаючими.
Аналіз фізичної проблеми. Амплітуда коливань набагато менша від довжини нитки, тому можна вважати, що за одне коливання кулька проходить шлях, який дорівнює чотирьом амплітудам (4A).
Якщо визначити кількість коливань за 36 с, то можна знайти відстань, яку подолала кулька. Кількість коливань знайдемо, визначивши час одного коливання, тобто період коливань.
Задачу розв’язуватимемо в поданих одиницях.
Дано:
T1= 30 c
N1= 15
T2 = 36 c
A = 5 см
Знайти:
L – ?
Пошук математичної моделі, розв’язання.
Знайдемо період коливань: T = 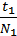 =
= 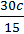 = 2 с.
= 2 с.
Знайдемо кількість коливань за 36 с: N2 = 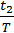 =
= 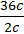 = 18.
= 18.
Визначимо шлях, який долає кулька за одне коливання: l0 = 4A = 4 ∙ 5 см = 20 см.
Визначимо шлях, який подолає кулька за 36 с:
L = N2 ∙ l0 = 18 ∙ 20 см = 360 см = 3,6 м.
Аналіз результатів. За одне коливання кулька проходить 20 см; час коливань більший за період коливань, тому пройдена кулькою відстань буде більшою за 20 см. Отже, результат є правдоподібним. Відповідь: l = 3,6 м.
Підбиваємо підсумки
Коливальний рух (коливання) є періодичним рухом. Розрізняють затухаючі і незатухаючі коливання.
Амплітуда А коливань – це фізична величина, що дорівнює максимальній відстані, на яку тіло відхиляється від положення рівноваги.
Період Т коливань – це фізична величина, що дорівнює часу, за який відбувається одне коливання: T =  . Одиниця періоду коливань в СІ – секунда (с).
. Одиниця періоду коливань в СІ – секунда (с).
Частота v коливань – це фізична величина, яка дорівнює кількості коливань за одиницю часу: v =  . Одиниця частоти коливань в СІ – герц (Гц).
. Одиниця частоти коливань в СІ – герц (Гц).
Частота і період коливань є взаємно оберненими величинами: v =  .
.
Контрольні запитання
1. Чому коливальний рух є періодичним? 2. Наведіть приклади коливань. 3. Наведіть приклади маятників. 4. Дайте означення амплітуди, періоду, частоти коливань. У яких одиницях вимірюють ці фізичні величини? 5. Яка залежність пов’язує між собою частоту і період коливань? 6. Які коливання називають затухаючими? незатухаючими?
Вправа № 13
1. Під час коливань тіло рухається від крайнього лівого положення до крайнього правого. Відстань між цими двома положеннями становить 4 см. Визначте амплітуду коливань тіла.
2. За хвилину маятник здійснив 30 коливань. Визначте період коливань маятника.
3. Період коливань дорівнює 0,5 с. Визначте частоту коливань.
4. Скільки коливань здійснить тіло за 2 хв, якщо частота його коливань становить 4 Гц?
5. Наведіть не згадані в параграфі приклади коливальних рухів. З’ясуйте, які це коливання: затухаючі або незатухаючі.
6. Поплавок, що коливається на воді, піднімається та пірнає 6 разів за 3 секунди. Який шлях подолає поплавок за хвилину, якщо відстань між його крайніми положеннями становить 5 см?
7. “Котра година?” – це питання ставлять протягом багатьох століть. Щоб відповісти на нього, існувало й зараз існує багато пристроїв. Один з них – маятниковий годинник. Дізнайтесь про історію його створення і підготуйте повідомлення.
Експериментальне завдання
“Резонанс”. Прив’яжіть до невеликого важкого тіла нитку завдовжки 45-50 см. Однією рукою візьміть нитку за вільний кінець, а другою відхиліть тіло від положення рівноваги. Маятник почне коливатися. Визначте частоту його вільних коливань.
Зупиніть маятник. Потім почніть дуже повільно рухати рукою з маятником з одного боку в інший (див. Малюнок). Слідкуйте, щоб амплітуда коливань руки не змінювалась; руку достатньо переміщувати на 1-2 см. Поступово збільшуйте частоту коливань руки і спостерігайте за маятником. “Спіймайте” такий момент, коли маятник розгойдається дуже сильно, тобто виникне резонанс. Визначте частоту коливань руки в той момент, коли амплітуда коливань маятника є найбільшою. Дізнайтеся, за якої умови настає резонанс, порівнявши знайдені значення частоти вільних коливань маятника і частоти коливань руки.

ЛАБОРАТОРНА РОБОТА № 5
Тема. Дослідження коливань нитяного маятника.
Мета: визначити амплітуду і період коливань нитяного маятника; переконатися на досліді, що період коливань маятника не залежить від амплітуди його коливань і маси тягарця, проте залежить від довжини нитки.
Обладнання: дві невеличкі важкі кульки відомих мас; дві міцні нерозтяжні нитки завдовжки 1,05-1,1 м; лінійка (мірна стрічка); штатив із муфтою та кільцем; секундомір.
ВКАЗІВКИ ДО РОБОТИ
Підготовка до експерименту
1. Перед тим як виконувати роботу, переконайтеся, що ви знаєте відповіді на такі запитання:
1) Що називають амплітудою коливань?
2) За якою формулою можна обчислити період коливань?
2. Визначте ціну поділки шкали лінійки.
3. Запишіть значення мас кульок до табл. 2.
4. Закріпіть кульки на нитках.
Експеримент. Опрацювання результатів експерименту
Суворо дотримуйтесь інструкції з безпеки (див. форзац підручника).
1. Установіть на краю стола штатив. Біля його верхнього кінця закріпіть за допомогою муфти кільце й підвісьте до нього одну з кульок на нитці так, щоб довжина одержаного маятника становила 1 м. Пересуваючи муфту вздовж штатива, установіть її на такій висоті, щоб кулька була на відстані 3-5 см від розташованої на підлозі лінійки (див. Малюнок).
2. Дослідіть залежність періоду коливань маятника від його амплітуди. Для цього:
1) відхиливши маятник на відстань 2-3 см від положення рівноваги і відпустивши, виміряйте час, за який маятник виконає 20 коливань; визначте період коливань;
2) повторіть дослід, збільшивши амплітуду коливань до 5-6 см;
3) результати вимірювань та обчислень занесіть до табл. 1.

Таблиця 1
Номер досліду | Довжина нитки l, м | Амплітуда коливань A, м | Число коливань N | Час коливань t, с | Період коливань T, с |
1 | 1 | ||||
2 | 1 |
3. Дослідіть залежність періоду коливань маятника від його маси. Для цього:
1) перенесіть із табл. 1 до табл. 2 результати досліду № 1;
2) повторіть дослід для другого маятника (іншої маси); амплітуда коливань має становити 2-3 см. Зверніть увагу: довжини першого та другого маятників мають бути однаковими.
3) результати вимірювань і обчислень занесіть до табл. 2.
Таблиця 2
Номер досліду | Довжина нитки l, м | Маса кульки m, кг | Число коливань N | Час коливань t, с | Період коливань T, с |
1 | 1 | ||||
3 | 1 |
4. Дослідіть залежність періоду коливань маятника від його довжини. Для цього:
1) перенесіть із табл. 1 до табл. 3 результати досліду № 1;
2) повторіть дослід, зменшивши довжину першого маятника до 25 см; амплітуда коливань має становити 2-3 см;
3) результати вимірювань і обчислень занесіть до табл. 3.
Таблиця 3
Номер досліду | Довжина нитки l, м | Число коливань N | Час коливань t, с | Період коливань T, с |
1 | 1 | |||
4 | 0,25 |
Аналіз експерименту та його результатів
Проаналізувавши результати, зробіть висновок, у якому зазначте: 1) які величини ви навчилися вимірювати; 2) які чинники вплинули на точність одержаних результатів; 3) чи залежить період коливань маятника від амплітуди коливань, маси тягарця, довжини маятника.
Творче завдання
Не виконуючи вимірювань, визначте період коливань маятника завдовжки 4 м, амплітуда коливань якого 10 см, а маса – 300 г. Вважайте, що маятник розташований у тому самому кабінеті, де ви виконували лабораторну роботу. Свою відповідь обгрунтуйте.
ПІДБИВАЄМО ПІДСУМКИ РОЗДІЛУ 2 “Механічний рух”
У розділі 2 ви вивчали механічний рух та його характеристики, дізналися про види механічного руху – прямолінійний рух, рух по колу, коливальний рух.
1. Ви ознайомились із деякими основними поняттями механіки.

2. Ви навчилися розрізняти види механічного руху.

3. Ви навчилися досліджувати рівномірний рух за допомогою графіків шляху та графіків швидкості руху.

4. Ви дослідили деякі механічні рухи.
Форма траєкторії | Фізичні величини, які характеризують механічний рух | ||
Шлях l [ l ] = м | Час руху t [ t ] = c | Швидкість руху v [ v ] = м/с | |
Рівномірний рух | |||
Будь-яка лінія | L = vt | T = | V = |
Рівномірний прямолінійний рух | |||
Пряма лінія | L = s = vt | T = | V = |
Нерівномірний рух | |||
Будь-яка лінія | L = l1 + l2 + … + ln | T = t1 + t2 + … + tn | V = |
Форма траєкторії | Фізичні величини, які характеризують механічний рух | ||
Період T [ T ] = с | Частота n або v [ n ] = об/с; [v] = Гц | Шлях за період l [ l ] = м | |
Рівномірний рух по колу | |||
Коло | T = | N = | L = 2 пR, Де R – радіус кола |
Коливальний рух | |||
Відрізок прямої, дуга кола | T = | V = | L0 = 4 A, Де А – амплітуда коливань |
Завдання для самоперевірки до розділу 2 “Механічний рух”
У завданнях 1-9 виберіть одну правильну відповідь.
1. (1 бал) Потяг, який прямує від однієї станції до іншої, перебуває у стані спокою відносно:
А) центра Землі;
Б) пасажира, що сидить у кріслі вагона;
В) точок на ободі колеса вагона;
Г) рейок, по яких він рухається.
2. (1 бал) Швидкість рівномірного руху – це фізична величина, яка дорівнює:
А) добутку шляху, який подолало тіло, і часу руху;
Б) відношенню часу руху до шляху, який подолало тіло;
В) половині суми початкової та кінцевої швидкостей руху;
Г) відношенню шляху, який подолало тіло, до часу руху.
3. (1 бал) Обертова частота – це фізична величина, яка чисельно дорівнює:
А) часу одного оберту;
Б) кількості обертів за одиницю часу;
В) кількості обертів за весь час руху;
Г) часу, за який тіло здійснює 10 обертів.
4. (1 бал) Період малих коливань нитяного маятника:
А) залежить від довжини нитки;
Б) залежить від маси тягарця;
В) залежить від амплітуди коливань;
Г) не залежить від земного тяжіння.
5. (2 бали) Космічний корабель протягом 20 с рухався зі швидкістю 10 000 м/с. Яку відстань подолав корабель за цей час?
А) 5 км; б) 20 км; в) 200 км; г) 500 км.
6. (2 бали) Потяг рухався із середньою швидкістю 40 м/с. Скільки часу тривала подорож між двома містами, якщо відстань між ними 624 км? а) 1 год 34 хв; б) 4,2 год; в) 4 год20 хв; г) 15,6 год.
7. (2 бали) Гвинт гелікоптера за 0,5 хвилини здійснює 600 обертів. Чому дорівнює період обертання гвинта?
А) 0,8 мс; б) 50 мс; в) 5 с; г) 2 хв.
8. (2 бали) Частота коливань нитяного маятника дорівнює 2 Гц. Скільки коливань здійснює цей маятник за 1 хв?
А) 0,5; б) 2; в) 30; г) 120.
9. (3 бали) Півгодини хлопчик їхав на велосипеді зі швидкістю 24 км/год, а потім ішов пішки 6 км зі швидкістю 4 км/год. Визначте середню швидкість руху хлопчика.
А) 9 км/год; б) 14 км/год; в) 20 км/год; г) 28 км/год.
10. (3 бали) За графіком залежності шляху від часу для рівномірного руху (рис. 1) визначте швидкість руху тіла. Відповідь подайте в м/с і км/год.
11. (3 бали) У кают-компанії судна, яке здійснює морську подорож у 250 км, розташований годинник. Скільки коливань здійснить маятник годинника за час подорожі, якщо період його коливань дорівнює 0,5 с, а середня швидкість руху судна – 10 м/с?

Рис. 1
12. (3 бали) Турист ішов гірською стежкою, рухаючись зі швидкістю 2 км/год, а потім повернувся до місця свого старту, рухаючись зі швидкістю 6 км/год. Якою була середня швидкість руху туриста на всьому шляху?
13. (4 бали) Використовуючи дані рис. 2, визначте, через який час зустрінуться автомобілі.
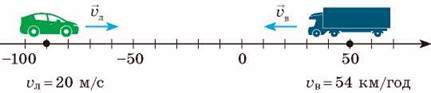
Рис. 2
14. (4 бали) На рис. 3 наведено графік швидкості руху автомобіля. Визначте максимальну швидкість руху автомобіля та весь шлях, що він подолав.
15. (5 балів) Автомобіль подолав 400 км. Відомо, що першу половину всього часу руху він рухався зі швидкістю 90 км/год, а за другу половину часу руху проїхав 175 км. Якою була швидкість руху автомобіля на другій ділянці шляху? Визначте середню швидкість руху автомобіля на всьому шляху. Рух автомобіля на обох ділянках вважайте рівномірним.

Рис. 3
Звірте ваші відповіді з наведеними наприкінці підручника. Позначте завдання, які ви виконали правильно, і полічіть суму балів. Потім цю суму поділіть на три. Одержане число відповідатиме рівню ваших навчальних досягнень.
Тренувальні тестові завдання з комп’ютерною перевіркою ви знайдете на електронному освітньому ресурсі “Інтерактивне навчання”.
Космодром на екваторі
Практично всі технічні новинки, що з’явилися за останні сто років, створено за такою схемою: етап 1 – учені відкривають новий ефект (явище); етап 2 – інженери-фахівці створюють пристрій (прилад), дія якого базується на використанні відкритого ефекту (явища).
Таким чином, інженери-механіки працюють над створенням нових, удосконалених автомобілів і верстатів, інженери-оптики – фотоапаратів і телескопів, інженери-електрики – акумуляторів і електромоторів тощо.
Прочитавши енциклопедичні сторінки в цьому підручнику, ви переконаєтеся в тому, що інженерові потрібні знання не тільки зі своєї спеціальності – він має широко застосовувати відомості з інших наукових галузей.
Як найдалі кинути камінь, або Чому космодроми будують поблизу екватора
Більшість жителів Землі гадки не мають, як улаштовані ракети й космічні станції, але майже всім відомо, що космос – це дуже багато витрат. Знають про це й інженери – конструктори ракет. І щоб зменшити, наприклад, витрати на доправлення вантажів на орбіту, вони намагаються знаходити в тому числі всілякі нетрадиційні рішення. Наведемо приклад.
Згадайте ваші ігри на дитячій каруселі: ви розганяєте карусель і застрибуєте на неї. При цьому найскладніше втримуватися на краю каруселі, що швидко обертається, – “невідома сила” намагається скинути вас. Саме цей фізичний ефект використовують спортсмени – метальники молота, розкручуючи металеве ядро на тросі (цікаво, що світовий рекорд у метанні молота приблизно в чотири рази більший, ніж у штовханні ядра, – близько 86 м і 22 м відповідно, при цьому маси обох снарядів є однаковими); на тому самому ефекті грунтується дія пращі – давньої метальної зброї.


Космічні кораблі виводитиме на орбіту ракета-носій “Циклон-4”
Конструктори ракет напевне добре знали фізику, адже вирішили “полегшити” старт космічного корабля, використовуючи як карусель Землю. І ось як. Відомо, що Земля обертається навколо своєї осі, при цьому зрозуміло, що найшвидше обертаються території навколо екватора. Запускаючи ракету з екватора, за інших однакових умов на орбіту можна “закинути” приблизно на 20% більше корисного вантажу. Тому, наприклад, космодром Європейського космічного агентства – космодром Куру – розміщений у Французькій Гвіані, безпосередньо поблизу екватора.
А що ж робити тим країнам, які розташовані в середніх широтах, наприклад Україні?
Майже 20 років тому почався грандіозний міжнародний проект за участю України, що отримав назву “Сі-Лонч” (у перекладі з англійської – “Морський старт”). Інженери вирішили: якщо країни не мають суходільної території на екваторі, слід здійснювати запуски ракет із морської поверхні. Як же цю ідею було реалізовано?
Зрозуміло, що для розміщення космодрому потрібна значна територія, практично цілий штучний острів. На щастя, подібні “острови” вже були створені, щоправда з іншою метою, – це плавучі платформи для видобутку нафти зі дна морів. Як ракета-носій у проекті “Сі-Лонч” була використана українська ракета “Зеніт” – одна з найкращих у світі. У рамках проекту було здійснено 36 пусків.
Українські фахівці одночасно з участю в “Морському старті” працювали в спільному українсько-бразильському проекті зі створення пускового майданчика на космодромі Алкантара (на півдні Бразилії, 300 км до екватора).
І знову “родзинкою” проекту з українського боку була ракета-носій. Цього разу – “Циклон-4”.

Місце розташування бразильського космодрому Алкантара

Ракети-носії українського виробництва
Теми рефератів і повідомлень
1. Еволюція приладів для вимірювання часу.
2. Способи відліку часу. Календарі.
3. Надшвидкі потяги світу.
4. Рекорди швидкості серед живих істот і серед технічних пристроїв. Порівняння.
5. Історія рекордів швидкості на суднах.
6. Історія рекордів швидкості на автомобілях.
7. Яким буде транспорт майбутнього.
8. Україна – космічна держава.
9. Марсіанська наукова лабораторія: марсохід “К’юріосіті”.
10. Комета Чурюмова – Герасименко.
11. Обертальний рух у природі й техніці.
12. Роль маятника у вивченні фізичних властивостей Землі.
Теми експериментальних досліджень
1. Вимірювання часу реакції людини.
2. Визначення середньої швидкості руху людини під час прогулянки.
3. Визначення середньої швидкості польоту м’яча.
4. Побудова графіків механічного руху паперового літачка та визначення середньої швидкості його руху.
5. Коливальні процеси в живій природі.
6. Коливальні процеси в техніці.
7. Коливальні процеси в неживій природі.


 =
=