Математичні вирази
Мета: узагальнити й систематизувати навчальний досвід учнів відносно математичних виразів: числових і виразів зі змінною; обчислення значень виразів.
Дидактичні задачі. Вдосконалювати обчислювальні навички позатабличного множення та ділення – усна лічба. Актуалізувати знання про математичні вирази: числові і вирази зі змінною. Актуалізувати уміння застосовувати правила порядку виконання дій у числових виразах на кілька арифметичних дій та уміння знаходити значення виразів на кілька дій. Актуалізувати
Розвивальна задача: розвивати логічне мислення учнів (№8, 10).
ХІД УРОКУ
І. МОТИВАЦІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ
З першого класу ми працюємо з математичними виразами: читаємо, знаходимо їх значення. В 1-му класі – це були нескладні математичні вирази – сума та різниця. В 2-му класі до них додалися ще й вирази – добуток та частка, ми познайомились із дужками і правилами порядку виконання дій у виразах з дужками та без дужок. Також у 2-му класі вперше з’явилися вирази, що містили змінну, і ми навчалися знаходити їх значення. Сьогодні на уроці ми повторимо все, що нам відомо про математичні вирази.
ІІ. УЗАГАЛЬНЕННЯ Й СИСТЕМАТИЗАЦІЯ ВИВЧЕНОГО
1.Усна лічба.
Завдання №1 з робочого зошита.
2. Усне опитування.
Питання для усного опитування, подані на уроці №3. Додатково: Як називається вираз, якщо між числами стоїть знак “+”; “-“, “*”, “:”? Що треба зробити, щоб записати суму двох чисел; різницю двох чисел; добуток двох чисел; частку двох чисел? Що треба зробити, щоб знайти значення суми, різниці, добутку, частки?
3. Актуалізація поняття числового виразу.
Завдання №1 виконується колективно.
Читаємо вирази сума ( різниця; добуток; частка) чисел 14 та 7. Читаючи складніші вирази, визначаємо, яка дія виконується останньою й пригадуємо назви її компонентів: зменшуване 56, від’ємник поданий добутком чисел 13 і 3; або від числа 56 відняти добуток чисел 12 і 3…
З’ясовуємо, що всі ці записи складаються з чисел, які з’єднані знаками арифметичних дій та дужками – це числові математичні вирази.
Значення числових виразів можна обчислити. Пропонуємо учням знайти значення виразів. Очевидно, що для перших двох стовпчиків виразів, щоб знайти значення, достатньо виконати арифметичну дію, знак якої записаний між числами. Для знаходження значень виразів останнього стовпчика треба пригадати правила порядку виконання дій у виразах.
4.Актуалізація правил порядку виконання дій у виразах та уміння знаходити значення числових виразів на кілька дій.
Завдання №2 виконується з коментарем.
Учні, користуючись правилами порядку виконання дій у виразах, визначають порядок дій і поступово, використовуючи усні прийоми обчислення, а за потреби й письмове додавання і віднімання, знаходять значення числових виразів.
5. Застосування законів та правил арифметичних дій для тотожних перетворень математичних виразів.
Завдання №2 із робочого зошита виконується з коментарем.
6.Застосування уміння знаходити значення виразів на кілька дій при порівнянні числових виразів.
Завдання №3 виконується учнями самостійно з наступною взаємоперевіркою.
7.Узагальнення поняття про математичні вирази. Актуалізація поняття про вирази зі змінною.
Завдання №4 виконуються колективно.
Орієнтуємось на ознаку наявності у вирази букви – змінної чи її відсутності. Маємо у одній групі числові вирази, а в іншій ті, що містять змінну – вирази зі змінною. Значення числових виразів знайти легко, виконавши відповідні арифметичні дії між числами, а значення виразів зі змінною знайти неможливо, оскільки не дано значення змінної.
8.Актуалізація способу міркування із знаходження значення виразу зі змінною.
Завдання №5 виконується з коментарем.
Вираз, що містить змінну чи змінні – є виразом зі змінною. Щоб знайти значення виразу зі змінними, треба знати яких числових значень набувають змінні та підставити їх у вираз. Очевидно, що значення виразу зі змінними залежить від числових значень змінних; змінна може набувати не одне числове значення, а кілька, тому значення виразу зі змінною не є єдиним.
Якщо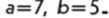 
, то
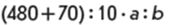= ( 480 + 70) : 10 * 7 : 5 =77
Очевидно, що підставивши значення змінних у вираз зі змінної, ми одержуємо числовий вираз, значення якого ми знаходимо дотримуючись правил порядку виконання дій.
9.Вдосконалення уміння знаходити значення виразів на кілька дій.
Завдання №6 виконується колективно.
При знаходженні значення першого виразу порушено правило порядку дій: дії множення та ділення виконуються в тому порядку, в якому вони записані – спочатку треба виконати ділення, а потім – множення. Аналогічної помилки припустилися у другому розв’язанні. При знаходженні значення третього виразу замість дії множення виконали дію додавання.
Завдання №7 виконується учнями самостійно з наступною взаємоперевіркою.
Завдання №8 пропонуємо учням з високим рівнем пізнавальних потреб і можливостей.
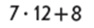Щоб значення добутку збільшилось, достатньо, щоб другий множник збільшився, тому суму 12 та 8 треба взяти у дужки.
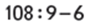Щоб значення частки збільшилось, достатньо, щоб дільник зменшився, тому різницю чисел 9 і 6 треба взяти у дужки.
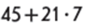Значення добутку ( 45 + 21)* 7 більше, ніж значення суми 45 + (21 * 7), тому треба взяти суму чисел 45 і 21 у дужки.
10.Вдосконалення обчислювальної навички ділення з остачею.
Завдання № 3 із робочого зошита – самостійна робота учнів.
11. Вдосконалення навичок письмового додавання і віднімання.
Завдання №4 із робочого зошита – самосійна робота учнів.
Зазначимо, що учні вміють виконувати перевірку правильності виконання додавання та віднімання двох чисел. Для випадку додавання трьох чисел у цей спосіб перевірити не можна: якщо від суми трьох доданків відняти один із доданків, то одержимо суму двох інших доданків.
12. Вдосконалення уміння розв’язувати задачі на знаходження четвертого пропорційного.
Завдання № 9 (1) – диференційована робота над задачею.
13. Розвиток вміння працювати з даними.
Завдання №11 виконується в парах або у малих групах.
14.Розвиток логічного мислення учнів.
Завдання №3 – пропонуємо для учнів з високим рівнем пізнавальних потреб і можливостей.
Розв’язання: 1) 13 – 5 = 8( м) було б в двох кусках, якби в них полотна було порівну; 2) 8 : 2 = 4 ( м) було б в кожному куску, якби в них полотна було порівну, стільки полотна в меншому куску; 3) 4 + 5 = 9 (м) – полотна у більшому куску. Перевірка: 9 + 4 = 13 (м).
УІІ. ПОЯСНЕННЯ ЗАВДННЯ ДЛЯ ДОМАШНЬОЇ РОБОТИ
Завдання №9 (2, 3). Треба уважно прочитати задачу, якщо вдасться, то “впізнати” її і пригадати узагальнений план розв’язування таких задач; якщо ні, то виконати аналітичний або синтетичний пошук розв’язування задачі.
УІІ. ПІДСУМОК. РЕФЛЕКСІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ
Які питання ви повторили, узагальнили сьогодні на уроці? Які види математичних виразів ви знаєте? Від чого залежить значення виразів зі змінною? Скільки значень може мати вираз зі змінною? Якими правилами користуються для знаходження значень виразів на кілька дій? Розкажіть про результати власних навчальних досягнень, починаючи висловлювання фразами: “Я розумію…”, “Я намагаюсь…”, “Я хочу досягти…”, “Я відчуваю, що мені потрібно…”.
(1 votes, average: 5.00 out of 5)
Loading...