МАТЕМАТИЧНИМ МАЯТНИК. ПЕРІОД КОЛИВАНЬ МАТЕМАТИЧНОГО МАЯТНИКА
МЕХАНІЧНІ І ЕЛЕКТРОМАГНІТНІ КОЛИВАННЯ І ХВИЛІ
Розділ 3 Коливання і хвилі
§ 22. МАТЕМАТИЧНИМ МАЯТНИК. ПЕРІОД КОЛИВАНЬ МАТЕМАТИЧНОГО МАЯТНИКА
З попередніх класів ви знаєте, що математичним маятником вважають точкове тіло, підвішене до нерозтяжної і невагомої нитки. Математичний маятник – це поняття абстрактне, тому що: розміри кульки набагато менші за довжину нитки, цими розмірами можна нехтувати і розглядати кульку як матеріальну точку. Розтягом нитки також можна нехтувати, оскільки він дуже малий. Можна нехтувати і масою нитки
Отже, з певним наближенням математичним маятником можна вважати кульку, підвішену на нитці (мал. 106). Рівняння руху математичного маятника має вигляд
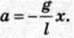
Разом з цим, розглядаючи рух проекції тіла, яке рівномірно обертається по колу, можна записати
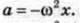
Прирівнюючи ці рівняння, отримаємо
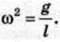
Протее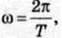 
тоді 
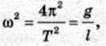звідки
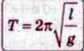
Ця формула для визначення періоду коливань математичного маятника була виведена і перевірена на дослідах
Період коливань математичного маятника залежить лише від прискорення вільного падіння в даному місці Землі і від довжини маятника. Період не залежить від амплітуди коливань і від маси підвішеного тягарця, що легко перевірити на дослідах з різними маятниками. Слід лише пам’ятати, що розміри тягарця мають бути малими порівняно з довжиною підвісу і що малим має бути також кут відхилення маятника від вертикалі. З наведеної залежності періоду коливань математичного маятника можна легко експериментально визначити прискорення вільного падіння. Для цього треба виміряти довжину маятника і період його коливань.
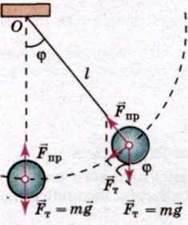
Мал. 106
Залежність періоду коливань математичного маятника від Прискорення вільного падіння використовується для точних вимірювань прискорення вільного падіння на поверхні Землі. Річ у тому, що прискорення вільного падіння в різних точках земної поверхні на одній і тій самій географічній широті є неоднаковим і залежить, хоча й незначно, від густини порід, з яких складаються верхні шари земної кори.
Усяке тіло, що має вісь обертання, яка не проходить через центр мас, здатне здійснювати коливання. Такі тіла називають фізичними маятниками. Нехай ми маємо тіло довільної форми, закріплене на осі обертання О (мал. 107). Центр мас цього тіла – точка С. Відстань від осі обертання до центра мас позначимо а. Якщо таке тіло вивести зі стану рівноваги і відпустити, то воно здійснюватиме коливання під дією рівнодійної сили тяжіння та сили пружності, що виникає в самому тілі. У будь-який момент часу рівнодійна сил напрямлена до положення рівноваги. Отже, маємо необхідні умови для виникнення коливань, як у разі коливань тягарця на пружині та математичного маятника. Формула для визначення періоду коливань фізичного маятника за аналогією з формулою для математичного маятника матиме такий вигляд:
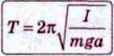
Де т – маса фізичного маятника; g – прискорення вільного падіння; а – відстань від осі обертання до центра мас маятника.
У формулу входить величина І, що характеризує інертні властивості тіл, які обертаються. Цю величину називають моментом інерції тіла відносно осі обертання.
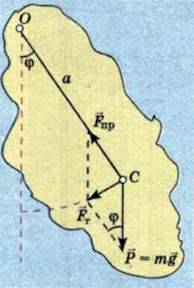
Мал. 107
(1 votes, average: 5.00 out of 5)
Loading...